属于内部排序 (4)归并排序
1. 抽出一张牌,和当前元素之前的元素逐个比较,如果比当前元素小,该元素就后移,直到找到插入位置 初始时视第一个元素是有序的 ,之后通过排序逐渐增大有序序列的长度while 循环 (更规范 )public static void insert_sort ( int [ ] arr) { for ( int i = 1 ; i < arr. length; i++ ) { int insertvalue = arr[ i] ; int j = i - 1 ; while ( j >= 0 && insertvalue < arr[ j] ) { arr[ j + 1 ] = arr[ j] ; j-- ; } arr[ j + 1 ] = insertvalue; }
}
for 循环 public static void insert_sort_1 ( int [ ] arr) { for ( int i = 1 ; i < arr. length; i++ ) { int insertvalue = arr[ i] ; int j = i - 1 ; for ( ; j >= 0 ; j-- ) { if ( insertvalue < arr[ j] ) { arr[ j + 1 ] = arr[ j] ; } else { break ; } } arr[ j + 1 ] = insertvalue; }
}
public static void binary_insert_sort ( int [ ] arr) { for ( int i = 1 ; i < arr. length; i++ ) { int insertvalue = arr[ i] ; int left = 0 ; int right = i - 1 ; while ( left <= right) { int mid = left + ( ( right - left) / 2 ) ; if ( arr[ mid] < insertvalue) { left = mid + 1 ; } else { right = mid - 1 ; } } for ( int j = i - 1 ; j >= right + 1 ; j-- ) { arr[ j + 1 ] = arr[ j] ; } arr[ right + 1 ] = insertvalue; }
}
最后 gap 的值必须是一 ,每一轮排序对 gap 产生的序列进行排序“ 1 ” 的位置全部替换 成 “ gap ”
public static void shell_sort ( int [ ] arr) { int gap = arr. length / 2 ; while ( gap >= 1 ) { shell ( arr, gap) ; gap /= 2 ; }
}
public static void shell ( int [ ] arr, int gap) { for ( int i = gap; i < arr. length; i++ ) { int insertvalue = arr[ i] ; int j = i - gap; while ( j >= 0 && insertvalue < arr[ j] ) { arr[ j + gap] = arr[ j] ; j -= gap; } arr[ j + gap] = insertvalue; }
}
public static void bubble_sort ( int [ ] arr) { for ( int i = 0 ; i < arr. length - 1 ; i++ ) { for ( int j = 0 ; j < arr. length - 1 - i; j++ ) { if ( arr[ j] > arr[ j + 1 ] ) { int temp = arr[ j] ; arr[ j] = arr[ j + 1 ] ; arr[ j + 1 ] = temp; } } }
}
改进版本 减少比较次数
public static void bubble_sort_improve ( int [ ] arr) { for ( int i = 0 ; i < arr. length - 1 ; i++ ) { int flag = 0 ; for ( int j = 0 ; j < arr. length - 1 - i; j++ ) { if ( arr[ j] > arr[ j + 1 ] ) { flag = 1 ; int temp = arr[ j] ; arr[ j] = arr[ j + 1 ] ; arr[ j + 1 ] = temp; } } if ( flag == 0 ) { break ; } }
}
把第一个元素当作枢纽,然后通过两个指针 left 和 right right : 在后面 找比枢纽小 的元素搬到 枢纽的前面 public static int partition ( int [ ] arr, int left, int right) { int pivot = arr[ left] ; while ( left < right) { while ( arr[ right] >= pivot && left < right) { right-- ; } arr[ left] = arr[ right] ; while ( arr[ left] <= pivot && left < right) { left++ ; } arr[ right] = arr[ left] ; } arr[ left] = pivot; return left;
} public static void quicksort ( int [ ] arr, int left, int right) { if ( left < right) { int pivot = partition ( arr, left, right) ; quicksort ( arr, left, pivot - 1 ) ; quicksort ( arr, pivot + 1 , right) ; }
}
最小的数 ,避免重复的覆盖,减少比较次数区别冒泡排序 的优化 冒泡排序 中是比较相邻两个元素之间 是否有序,如果有序就不交换位置 public static void select_sort ( int [ ] arr) { for ( int i = 0 ; i < arr. length; i++ ) { for ( int j = i + 1 ; j < arr. length; j++ ) { if ( arr[ j] < arr[ i] ) { int temp = arr[ j] ; arr[ j] = arr[ i] ; arr[ i] = temp; } } }
}
改进版本 public static void select_sort_improve ( int [ ] arr) { for ( int i = 0 ; i < arr. length; i++ ) { int min_index = i; for ( int j = i + 1 ; j < arr. length; j++ ) { if ( arr[ j] < arr[ min_index] ) { min_index = j; } } if ( min_index != i) { int temp = arr[ i] ; arr[ i] = arr[ min_index] ; arr[ min_index] = temp; } }
}
堆的性质是符合完全二叉树的,在结构上是递归定义的树结构 非叶子节点节点 的物理位置为 “ i ” 数组大小为 n (1)最后一个元素(叶子节点 )在树中的标号对应的数组下标是n / 2 从左到右,从上到下依次标号 对应数组下标 ) 0 / \1 2 / \ / \3 4 5 6
大根堆 :对于完全二叉树中的任意一个节点,其值都大于或等于其子树 中所有节点的值。这意味着大根堆的根节点是堆中最大的元素 10 / \8 6 / \ / \5 3 2
1 / \3 4 / \ / \6 8 9
堆排序思想 从后面的=第一个非叶子节点 (下标:n / 2 - 1 )开始,依次递归的往上调整,使得整棵树形成大根堆的结构 交换思想:交换的过程就是排序的过程,把最大的和最小的交换,即把最大的放入有序区,数组从后往前依次递减排序 理解:在调整过程中,指向的最大根节点会发生变化,对根节点调整即可实现对左右子树的调整 ) n - 1 的说明 (1)进行n - 1 趟排序 堆的大小的变化 ,每一轮排序一个元素(交换的过程),堆中需要调整的元素总数减小一
public static void heapify ( int [ ] arr, int n, int i) { int max_index = i; int left = 2 * i + 1 ; int right = 2 * i + 2 ; if ( left < n && arr[ left] > arr[ max_index] ) { max_index = left; } if ( right < n && arr[ right] > arr[ max_index] ) { max_index = right; } if ( max_index != i) { int temp = arr[ i] ; arr[ i] = arr[ max_index] ; arr[ max_index] = temp; heapify ( arr, n, max_index) ; }
}
public static void heap_sort ( int [ ] arr) { int n = arr. length; for ( int i = n / 2 - 1 ; i >= 0 ; i-- ) { heapify ( arr, n, i) ; } for ( int i = n - 1 ; i > 0 ; i-- ) { int temp = arr[ 0 ] ; arr[ 0 ] = arr[ i] ; arr[ i] = temp; heapify ( arr, i, 0 ) ; }
}
递归思想






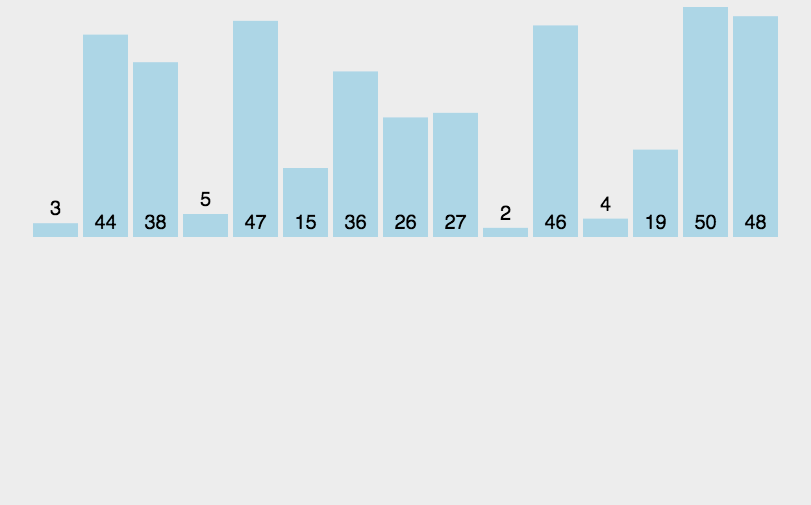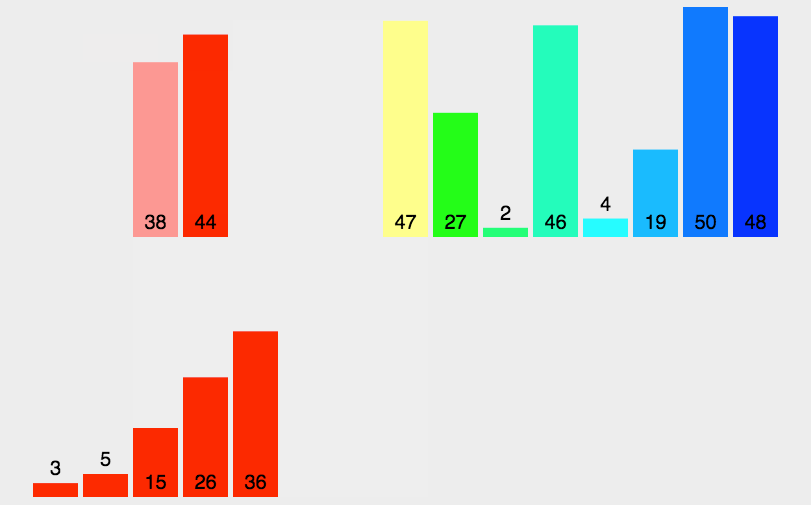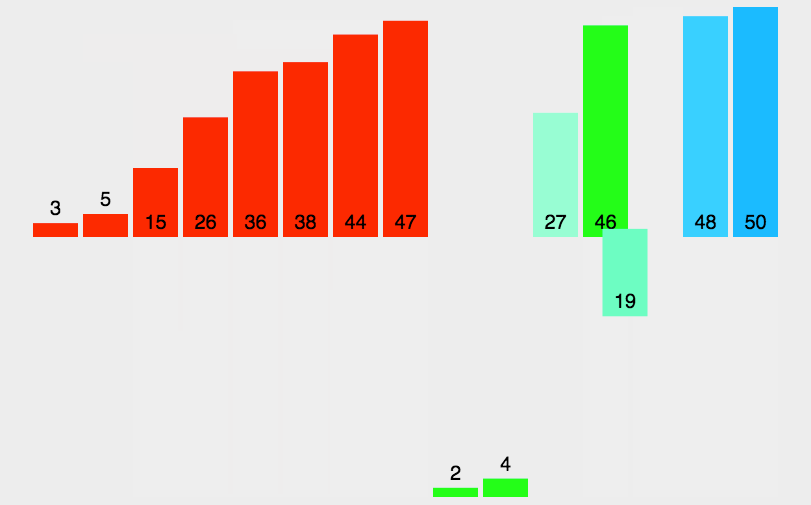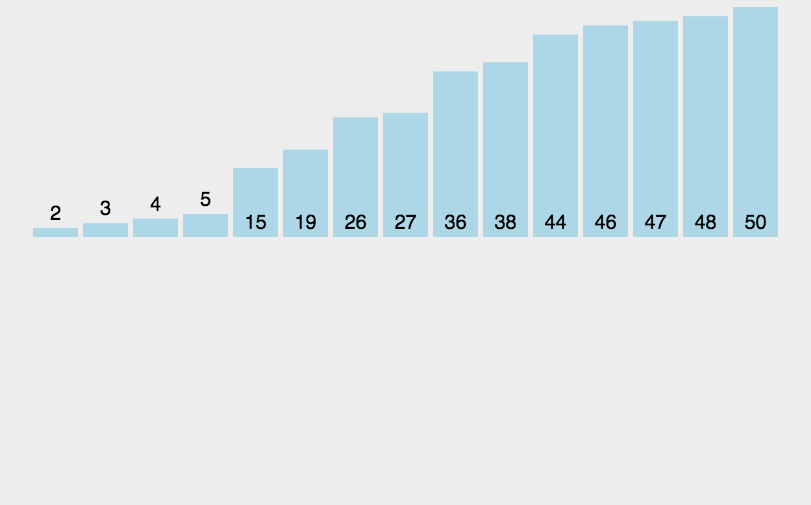


)

Step-Back 回答回退策略扩大检索范围)











)


