树

这是树（拍摄于郑州轻工业大学，第一次郑州轻工业新生赛~）
这是树的一些概念：

什么是二叉树

？？？

二叉树是n(n>=0)个节点的有限集合。

• 1.每个节点最多只有两个子树
• 2.左右子树不能颠倒
  （二叉树是有序树）

二叉树的五种状态

几种特殊的二叉树：

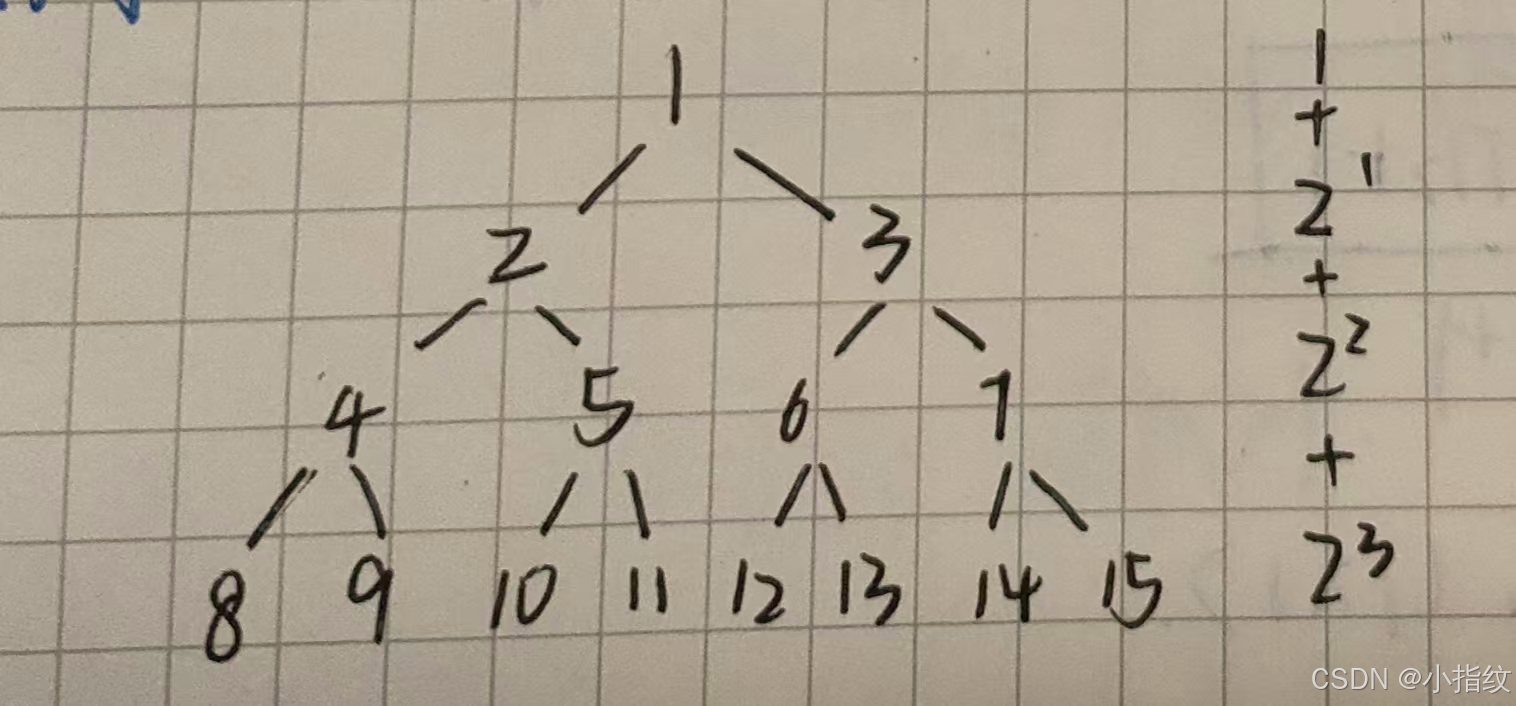
满二叉树

高度为h，且含有$2^h$-1个结点的二叉树
特点：

• 1.只有最后一层有叶子结点
• 2.不存在度为一的点
• 3.按层序从1开始编号结点i的左孩子为2i,右孩子为2i+1
  

完全二叉树

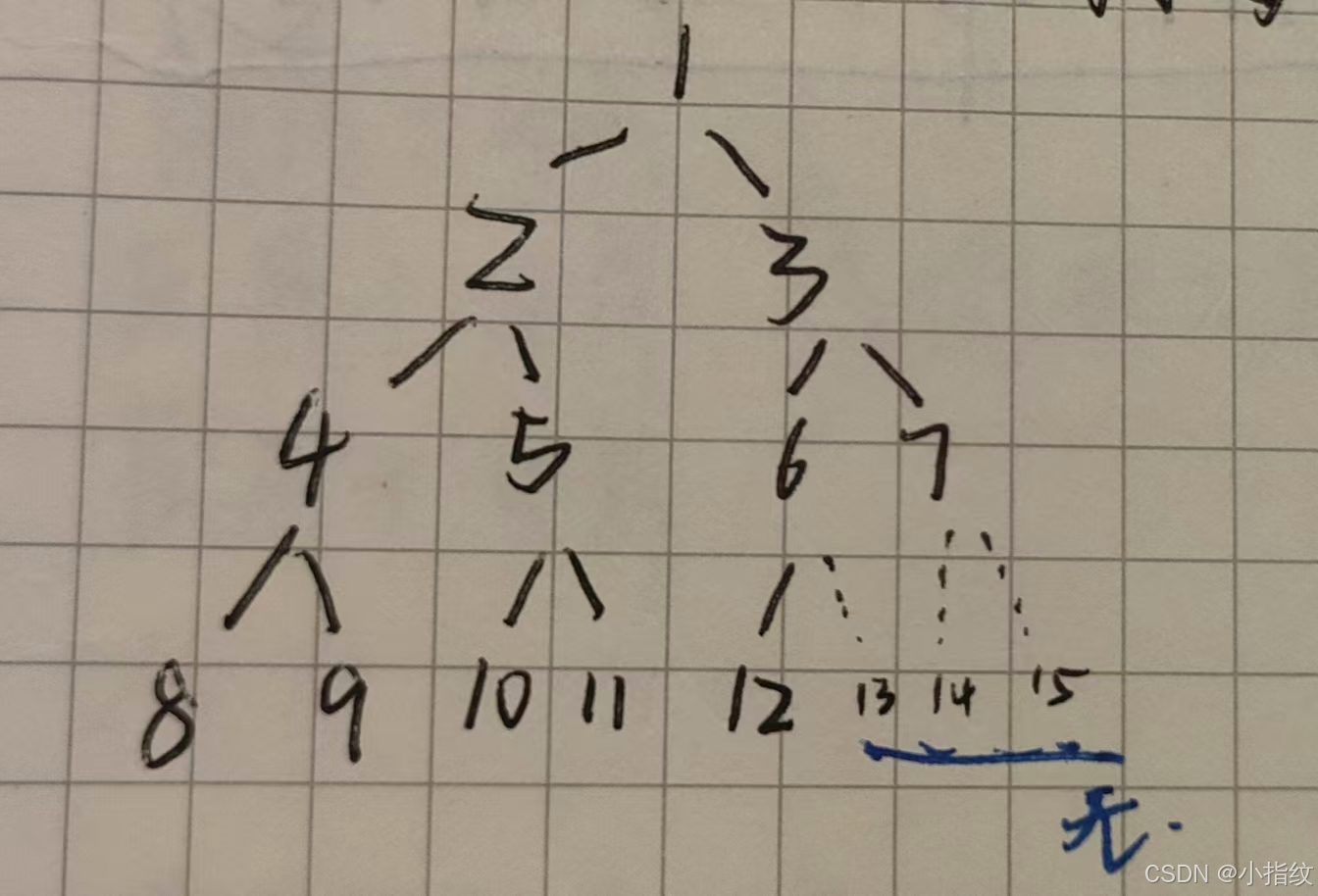
当且仅当其每个结点都与高度为h的满二叉树中编号问为1~n的结点一 一对应时成为完全二叉树。
特点

• 1.只有最后两层可能有叶子结点。
• 2.最多 只有一个度为1的结点。
• 3.按层序从1开始编号结点i的左孩子为2i,右孩子为2i+1
  

二叉排序树

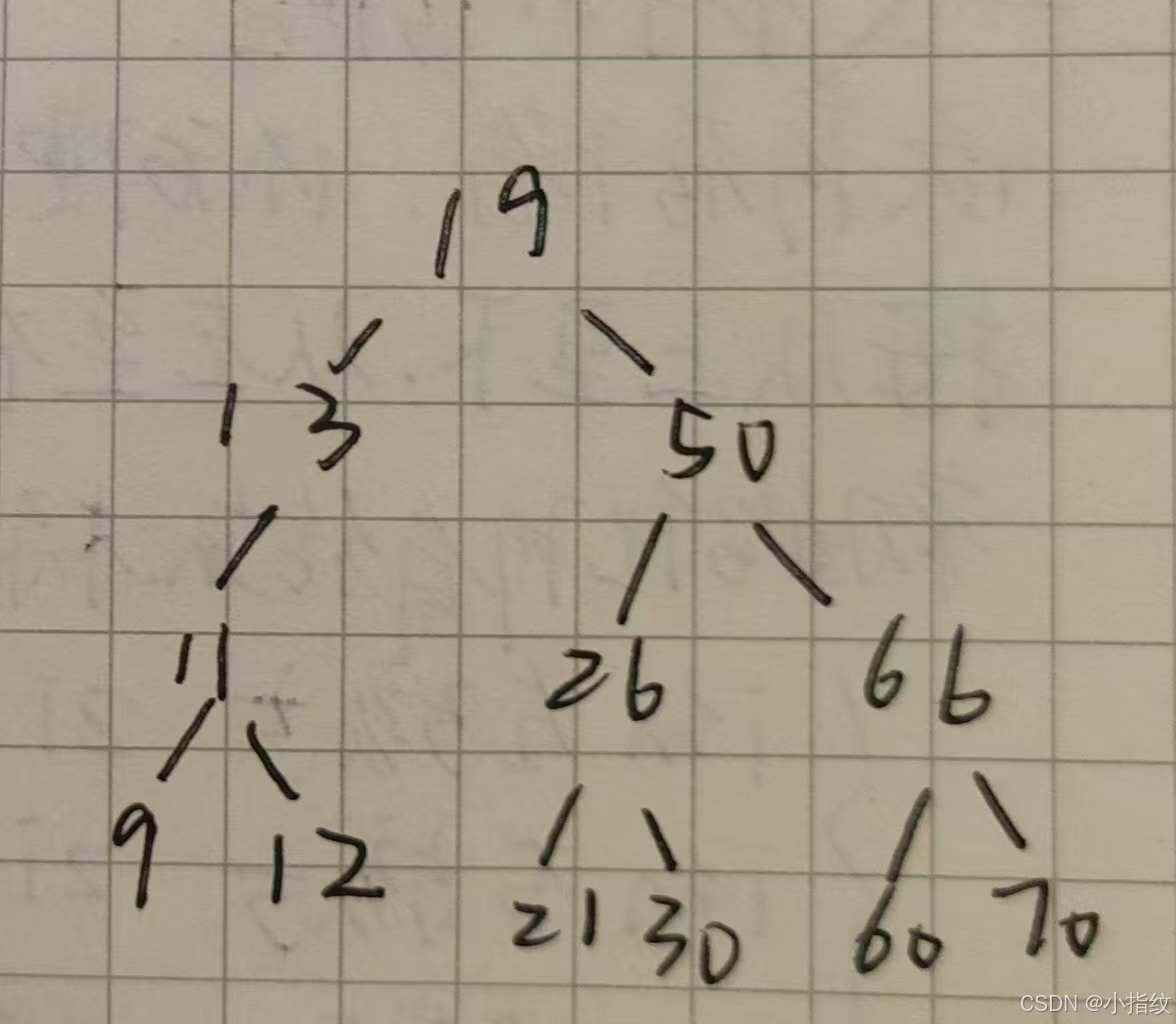
左子树上所有结点的关键字均小于根节点的关键字
右子树上所有结点的关键字均大于根节点的关键字
左子树和右子树又分别时一颗二叉排序树

平衡二叉树

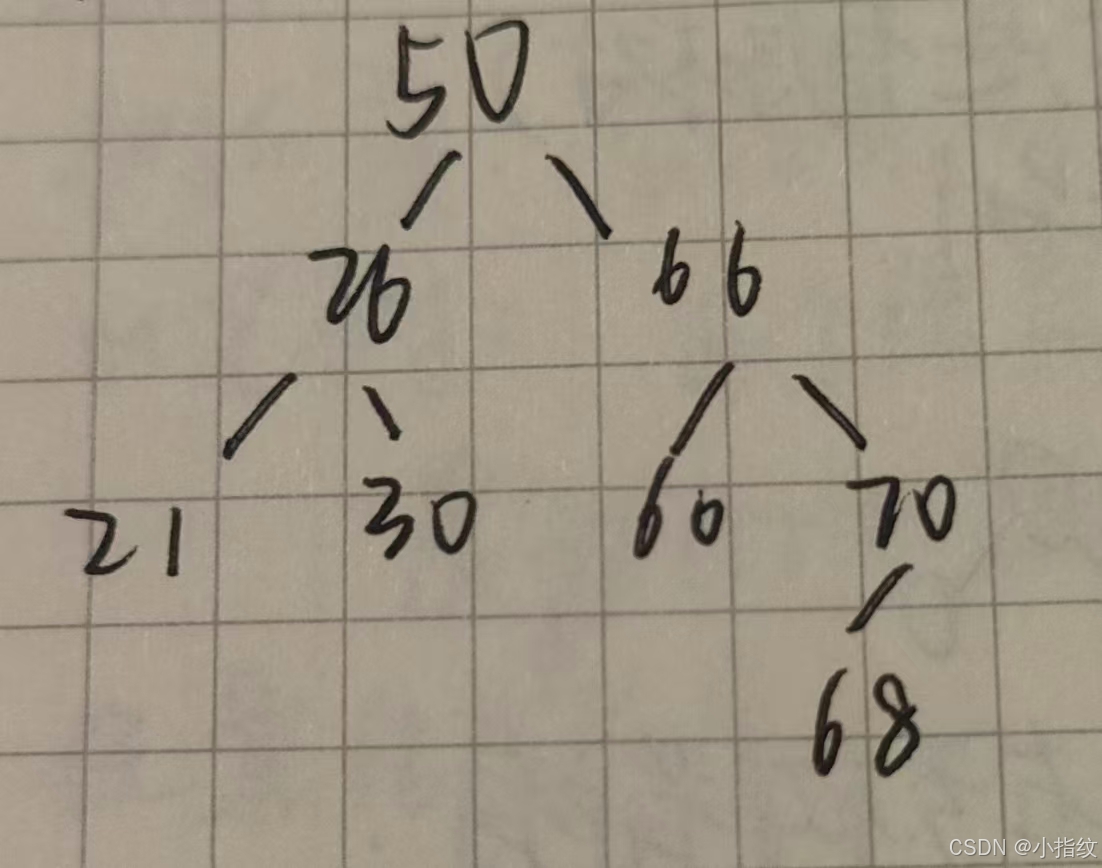
树上任一结点的左子树和右子树的深度之差不超过1
(有更高的搜索效率)

二叉树的遍历

前序遍历

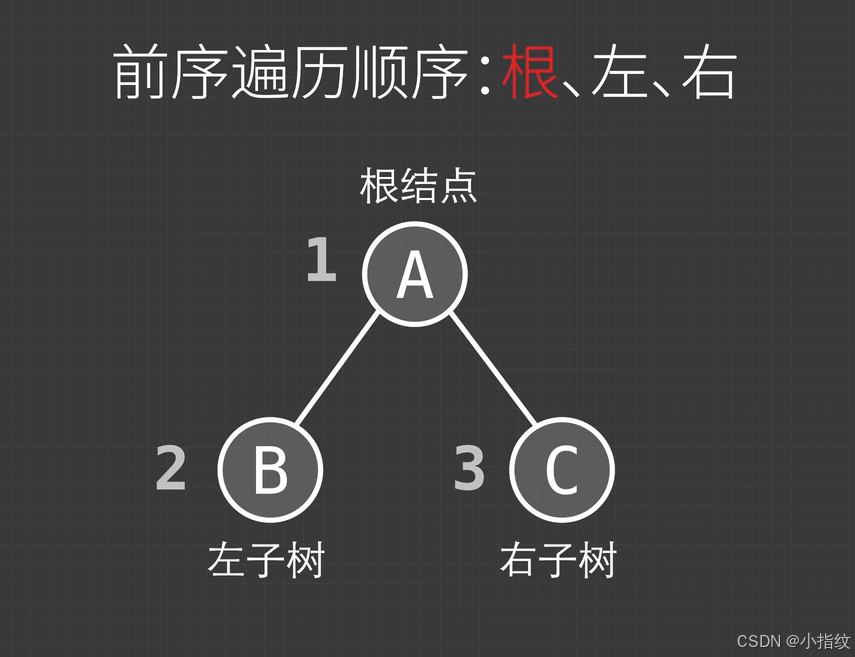
中序遍历

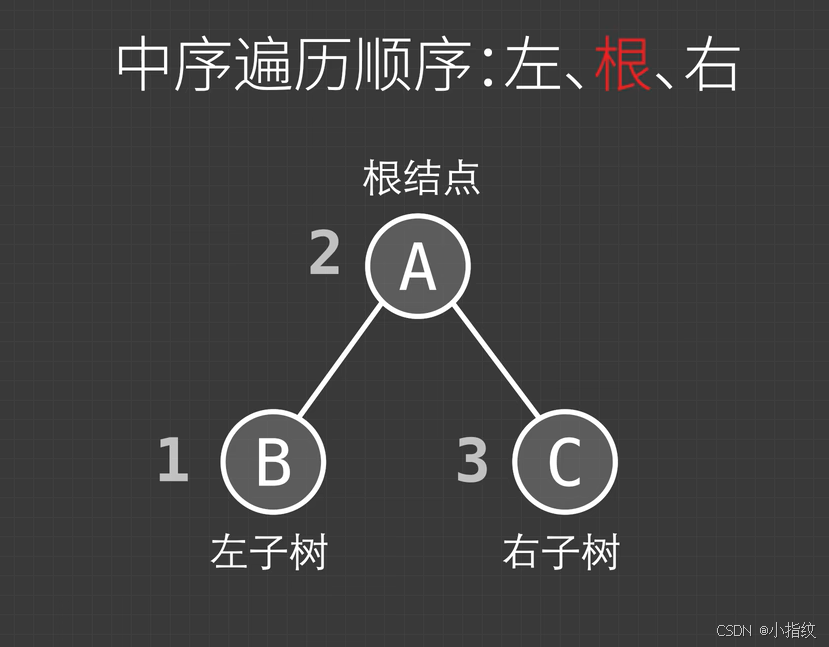
后序遍历

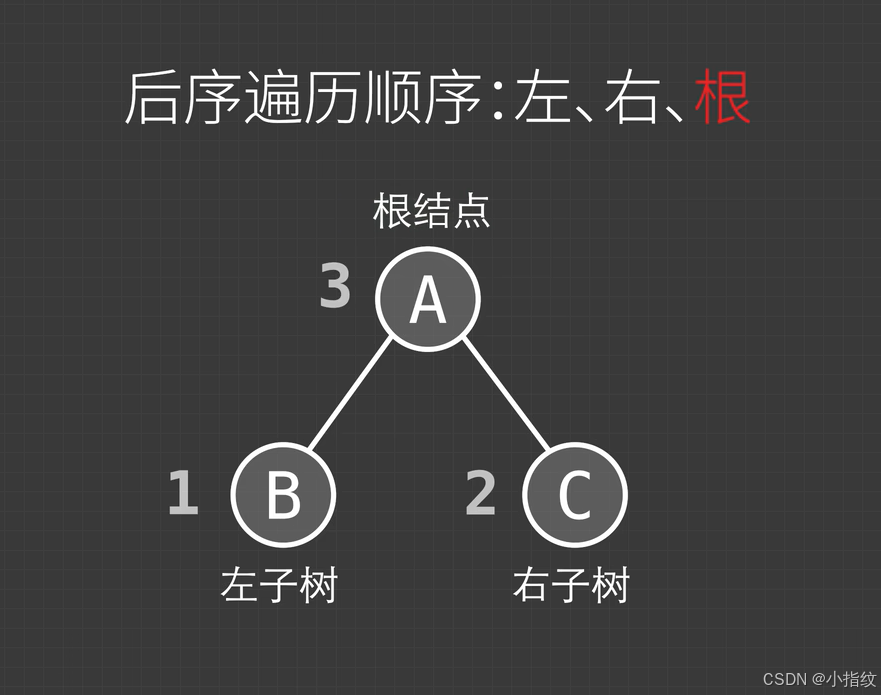
关于遍历二叉树，有一个巧妙的方法分享给大家。
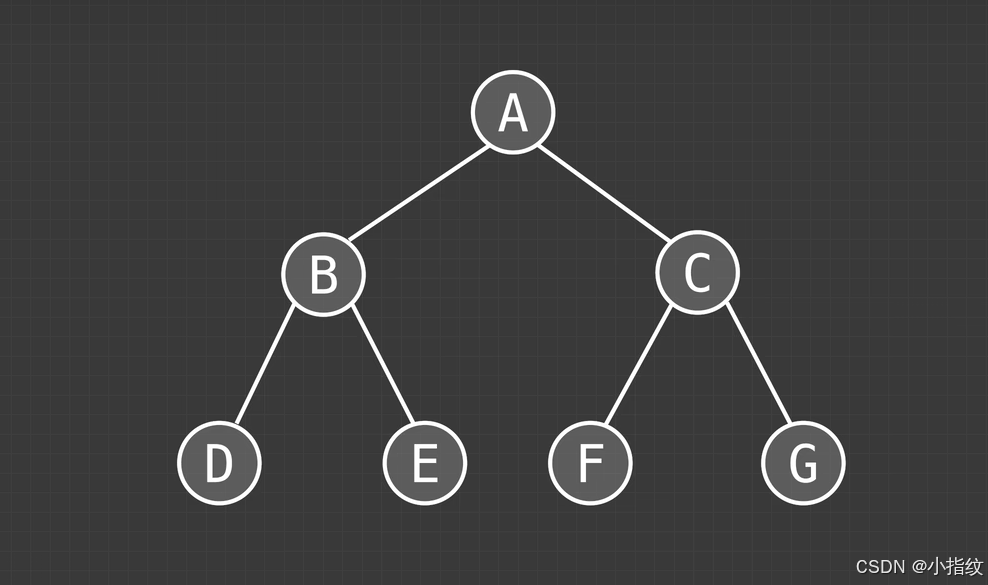
以下图为例：

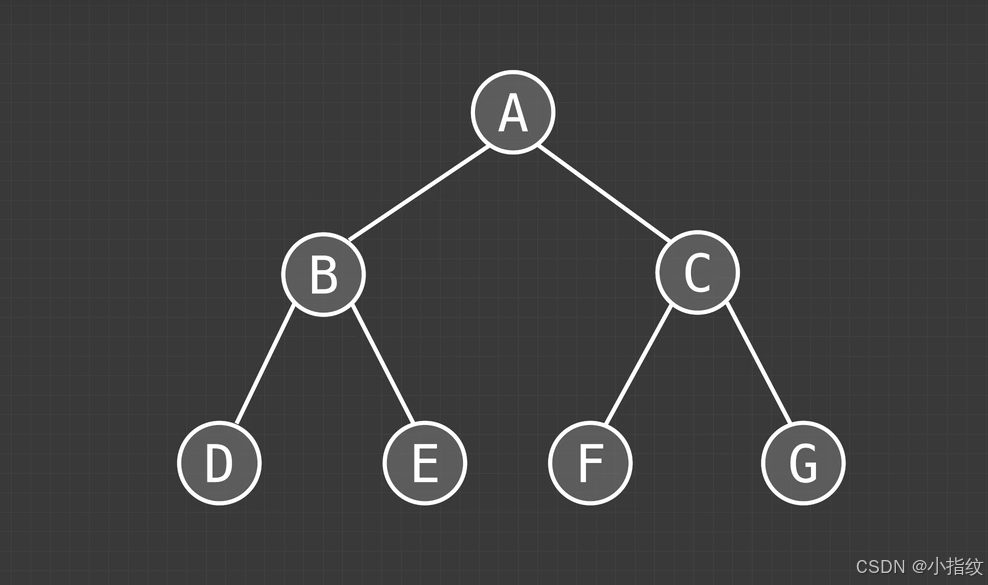
以中序遍历：左根右 为例：
我们可以先遍历最上边的ABC, 并给B和C的子节点留上位置
_ B _ A _ C _
然后再将B和C的子节点按左根右的顺序填上去
就是这个顺序：DBEAFCG
同理，你可以练习一下：
先序遍历：ABDECFG
后序遍历：DEBFGCA

有了以上的基础，我们拿道题练练手吧！

B3642 二叉树的遍历

B3642 二叉树的遍历

题目描述

有一个 $n(n\le 10^6)$ 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 $n$），建立一棵二叉树（根节点的编号为 $1$），如果是叶子结点，则输入 0 0。

建好树这棵二叉树之后，依次求出它的前序、中序、后序列遍历。

输入格式

第一行一个整数 $n$，表示结点数。

之后 $n$ 行，第 $i$ 行两个整数 $l$、$r$，分别表示结点 $i$ 的左右子结点编号。若 $l=0$ 则表示无左子结点，$r=0$ 同理。

输出格式

输出三行，每行 $n$ 个数字，用空格隔开。

第一行是这个二叉树的前序遍历。

第二行是这个二叉树的中序遍历。

第三行是这个二叉树的后序遍历。

输入 #1

7
2 7
4 0
0 0
0 3
0 0
0 5
6 0

输出 #1

1 2 4 3 7 6 5
4 3 2 1 6 5 7
3 4 2 5 6 7 1

这是一道很模板的二叉树遍历练习题，很适合新手宝宝体质，按顺序根据前序中序和后续的遍历顺序，结合深搜就可以很容易的输出顺序啦~代码注释很详细！

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+6;
int n,l[N],r[N];//l和r分别存左子节点和右子节点
//前序遍历，根左右  
void a(int x)//前序遍历访问到第x号点 
{if(x==0)return ;//题目中说这个结点为0时表示无此结点//然后就是按照前序遍历cout<<x<<" ";//先输出根a(l[x]);//再输出左子结点a(r[x]);//最后输出右子节点	
} 
//中序遍历，左根右
void b(int x)//中序遍历访问到第x号点 
{if(x==0)return ;//中序遍历 b(l[x]);//先输出左子结点cout<<x<<" ";//再输出根b(r[x]);//最后输出右子节点	
} 
//后序遍历，左右根
void c(int x)//后序遍历访问到第x号点 
{if(x==0)return ;//后序遍历顺序 c(l[x]);//先输出左子结点c(r[x]);//再输出右子节点	cout<<x<<" ";//最后输出根
} 
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>l[i]>>r[i];//输入对应位置的左右节点 //前序遍历，根左右 a(1);//根节点从1开始遍历cout<<endl;//前序遍历完后要输出换行//中序遍历，左根右b(1);//根节点也是从1开始中序遍历cout<<endl;//后序遍历，左右根c(1);cout<<endl; return 0;
} 

再来一道例题练练手吧！

P1305 新二叉树

P1305 新二叉树

题目描述

输入一串二叉树，输出其前序遍历。

输入格式

第一行为二叉树的节点数 $n$。($1\le n\le 26$)

后面 $n$ 行，每一个字母为节点，后两个字母分别为其左右儿子。特别地，数据保证第一行读入的节点必为根节点。

空节点用 * 表示

输出格式

二叉树的前序遍历。

输入 #1

6
abc
bdi
cj*
d**
i**
j**

输出 #1

abdicj

一道很基础的二叉树题，可以通过结构体将这个二叉树建立起来，虽然题目中给的字符，但同样可以存储在结构体数组中，因为字符ACS码最大不超过128，所以数组只需开150就足够，然后可以利用深搜，将第一个节点传入dfs，依次搜索，当子节点不为 * 时才继续往下搜。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
struct node//简单的建树 
{char l,r;
}p[150];
int n;
void dfs(char bg)
{cout<<bg;if(p[bg].l !='*') dfs(p[bg].l);//如果不为空节点就接着往下搜 if(p[bg].r !='*') dfs(p[bg].r);
}
void solve()
{cin>>n;char a,x,y,bg;cin>>a>>x>>y;bg=a;//作为初始深搜的点 p[a].l =x,p[a].r =y;//左右子数 n-=1;while(n--){cin>>a>>x>>y;p[a].l =x,p[a].r =y;}dfs(bg);
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

---

二叉树的深度

二叉树深度简而言之就是这个二叉树最多有几层

比如这个二叉树，它的深度就是3

我们直接上例题感受一下吧！

P4913 【深基16.例3】二叉树深度

题目描述

有一个 $n(n\le 10^6)$ 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 $n$），建立一棵二叉树（根节点的编号为 $1$），如果是叶子结点，则输入 0 0。

建好这棵二叉树之后，请求出它的深度。二叉树的深度是指从根节点到叶子结点时，最多经过了几层。

输入格式

第一行一个整数 $n$，表示结点数。

之后 $n$ 行，第 $i$ 行两个整数 $l$、$r$，分别表示结点 $i$ 的左右子结点编号。若 $l=0$ 则表示无左子结点，$r=0$ 同理。

输出格式

一个整数，表示最大结点深度。

输入 #1

7
2 7
3 6
4 5
0 0
0 0
0 0
0 0

输出 #1

4

思路分析

我们可以先利用结构体读入这个二叉树

• 拥有左子节点和右子节点两个参数的结构体
• 开n范围的结构体数组

搜索（dfs)

• 状态：当前走到什么编号的节点以及当前的深度
• 终止条件：走到0号节点（更新最大深度)
• 走到哪里去？当前所在编号的节点的左右子节点

输出最大深度

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
struct node//建树 
{int l,r;
}p[N];
int n,ans=INT_MIN;//ans用来记录树的最大深度 
void dfs(int x,int h)
{//终止条件：子节点为0时 ans=max(ans,h);//更新最大值 //走到哪里去if(p[x].l)//如果左子节点不为0 dfs(p[x].l,h+1);if(p[x].r)//如果右子节点不为0 dfs(p[x].r,h+1); 
}
void solve()
{cin>>n;for(int i=1;i<=n;i++)cin>>p[i].l>>p[i].r;dfs(1,1);//传入最初所在位置和最初深度cout<<ans; 
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

---

相关例题训练：

二叉树问题

P3884 [JLOI2009] 二叉树问题
题目描述

如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

• 深度：$4$
• 宽度：$4$
• 结点 8 和 6 之间的距离：$8$
• 结点 7 和 6 之间的距离：$3$

其中宽度表示二叉树上同一层最多的结点个数，节点 $u,v$ 之间的距离表示从 $u$ 到 $v$ 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

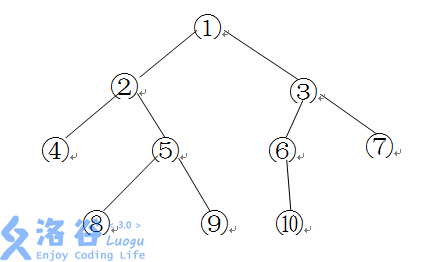
给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 $x,y$ 之间的距离。

输入格式

第一行是一个整数，表示树的结点个数 $n$。
接下来 $n-1$ 行，每行两个整数 $u,v$，表示树上存在一条连接 $u,v$ 的边。
最后一行有两个整数 $x,y$，表示求 $x,y$ 之间的距离。

输出格式

输出三行，每行一个整数，依次表示二叉树的深度、宽度和 $x,y$ 之间的距离。

输入 #1

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出 #1

4
4
8

说明/提示

对于全部的测试点，保证 $1\le u,v,x,y\le n\le 100$，且给出的是一棵树。保证 $u$ 是 $v$ 的父结点。

求深度

• 1.构建树，用结构体更方便
• 2.dfs对每个节点深度赋值
• 3.找到所有节点深度最大值

求宽度

• 1.统计每一层的宽度
• 2.求宽度最大值

求距离
BFS

AC代码

#include<bits/stdc++.h>
using namespace std;
struct node//建树 
{int l,r,f,d;//分别代表左子节点、右子节点、父节点和当前节点深度 
}ns[105];
struct node2//便于查找距离 
{int pos,step;
};
int dp=0,wd,wid[105],st[105];//分别表示当前最大深度、宽度，宽度数组和状态数组 
void dfs(int p)
{if(st[p])return ;//如果已经被访问过return st[p]=1;//标记为1 int le=ns[p].l ,ri=ns[p].r ,de=ns[p].d;//左子节点右子节点深度赋值 dp=max(dp,de);//更新最大深度 wid[de]++;//记录宽度 if(le)//如果有左子节点 {ns[le].d=de+1;//深度加1 dfs(le);//接着向下搜 }if(ri)//如果有右子节点 {ns[ri].d =de+1;dfs(ri);}
}
int main()
{int n,u,v,x,y;cin>>n;for(int i=1;i<n;i++)//n-1条边 {cin>>u>>v;if(!ns[u].l) ns[u].l =v;//如果没有左子节点存入左子节点 else ns[u].r =v;//否则存入右子节点 ns[v].f=u;//记得更新父节点 }cin>>x>>y;//输入要查找距离的两个点 ns[1].d =1; //第一个节点即初始深度为1 dfs(1);//传入当前位置节点 for(int i=1;i<=n;i++)//循环遍历找出最大宽度 wd=max(wd,wid[i]);cout<<dp<<endl<<wd<<endl;//输出最大深度和最大宽度 memset(st,0,sizeof(st));//将状态数组重置为0 node2 tn={x,0};//将初始点和距离值传入 st[x]=1;//状态改变表示已被访问过 queue<node2>q;//建立结构体状态数组 q.push(tn);//将初始状态传进去 while(!q.empty())//当队列不空时 {tn=q.front();//取队首元素 q.pop();//队首弹出 if(tn.pos==y)//当所查找的值到达y时 {cout<<tn.step;//输出距离 break;//查找结束 }int le=ns[tn.pos].l;int ri=ns[tn.pos].r;int fa=ns[tn.pos].f;int step=tn.step ;if(le&&!st[le])//如果左子节点不空并且没被访问过 {st[le]=1;//更新状态数组 q.push({le,step+1});//将更新后的位置和距离压入队列 }if(ri&&!st[ri])//以下同理 {st[ri]=1;q.push({ri,step+1});}if(fa&&!st[fa]){st[fa]=1;q.push({fa,step+2});//因为到父节点是向上走，所以每次更新两步 }} return 0;
}