一·线性回归
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
相关关系:包含因果关系和平行关系
因果关系:回归分析【原因引起结果,需要明确自变量和因变量】
平行关系:相关分析【无因果关系,不区分自变量和因变量】
二·一元线性回归模型理论
一元线性回归模型表达式为:y=β0+β1x+ε
其中:
0.
为模型参数,用于刻画自变量 x 与因变量 y 线性关系的截距和斜率 。
可以看成y=kx+b中的k而
则可以看看成b
为误差项,代表除线性因素外,由随机因素导致的误差 。
例子:
自变量:工资
因变量:贷款额度
工资到底能产生多大的影响呢?如何比较公平的评定工资的影响呢?
| 工资(x) | 贷款额度(y) |
|---|---|
| 4000 | 10000 |
| 8000 | 12000 |
| 5000 | 8000 |
| 3000 | 10000 |
| 6000 | 15000 |
| 7000 | ? |
三·多元线性回归模型
多元线性回归模型:
y=β0+β1x1+β2x2+ε
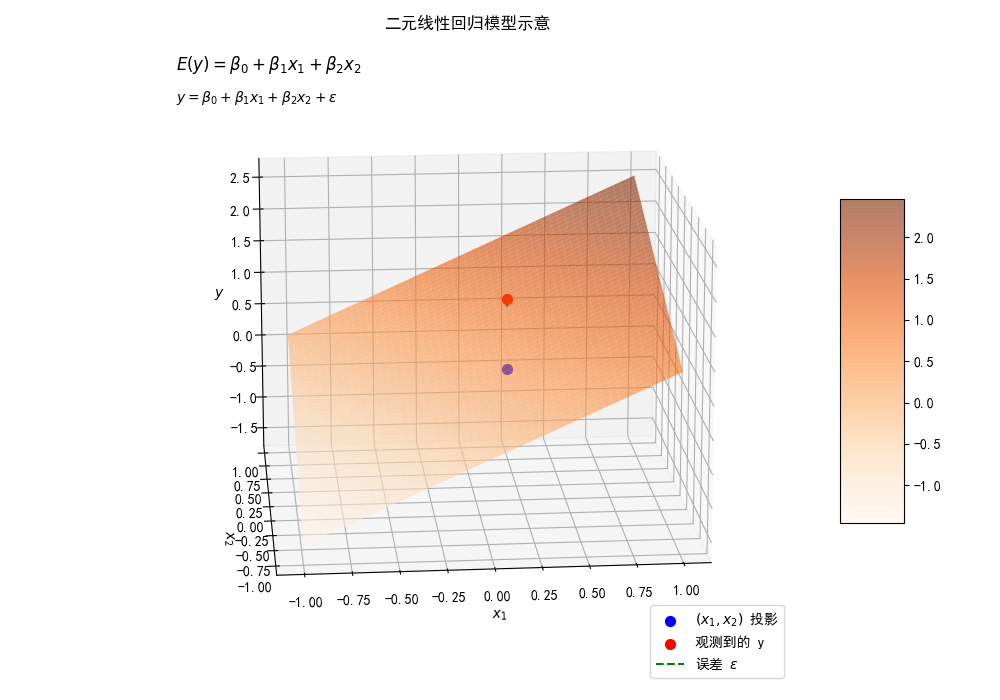
其中:
β0·β1·β2是模型参数。
是误差项。
误差项:除线性因素外的随机因素所产生的误差。
四·误差项分析
1. 误差项可以省略吗?
答:误差项不可省略,误差是必然产生的。并且由于产生了误差项,我们便可以基于误差的特点来进行对线性回归的参数估计的。
2. 误差项有什么特点?
答:独立同分布。
独立:每个样本点都是独立的;例:贷款,每个人与每个人之间是没有联系的,贷多少钱完全基于你的工资。
同分布:同分布就是我的这套估计体系是我人民银行的估计体系,每个人都是服从我的分布体系,不会使用别人的估计体系,也就是说每个样本点都处于同一个分布函数下。
3. 误差项满足高斯分布。
高斯分布:
又称为正态分布,概率密度函数为:
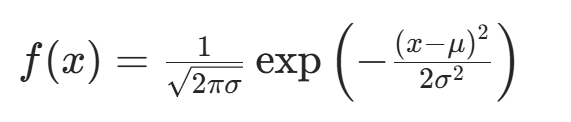
对参数问题的估计就转化成了对误差项的分析。
1. 期望为 0;
2. 方差相同,为
控制正态分布图像的高矮
4·误差项分析
误差项分析
线性回归的转化:
矩阵计算:
其中x0是1,目的是写成矩阵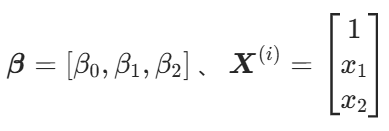
由于为样本项,为列向量,所以此处对
参数进行转置,转为行向量,从而得到以下结果。
其中T是右上标
矩阵计算——并行化计算
误差项分析
预测值与误差的最终的真实结果:
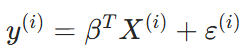
误差项满足高斯分布:
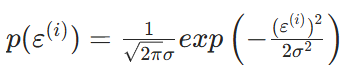
将误差带入高斯分布:
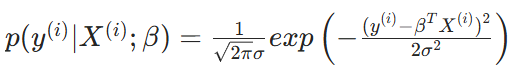
五·极大似然估计
极大似然估计是根据样本推测参数的方法。核心是找使样本出现概率最大的参数值,即“最可能”生成该样本的参数。通过构建似然函数,求其最大值点得到估计,广泛用于统计推断。
极大似然估计
假设一个袋子里面有10个球,你抽了一次,发现是黑球;接着又抽了一次,发现又是黑球;在10 次之后,你发现有9次是黑球,1次是白球,那么请问袋子里面黑球有几个?白球有几个?
黑球:9/10*10=9个
白球:1/10*10=1个
前提:规律你不知道。 通过事实的数据结果 得到规律
事实发生的事情,一定是最大概率的结果。
六·似然函数求解
似然函数:
一条数据存在一个概率,每条数据都存在这样一个概率,那么总的概率最大该怎么办呢?
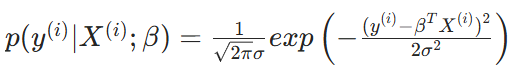
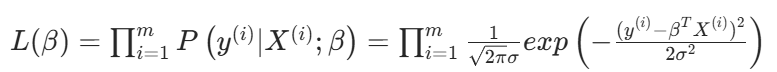
每个样本都是独立的,独立的概率最大,自然是连乘了
似然函数求解
可是连乘不好计算啊,怎么办呢?
对数似然函数:
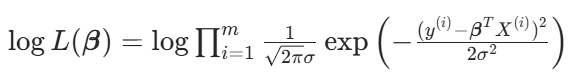
化简得:
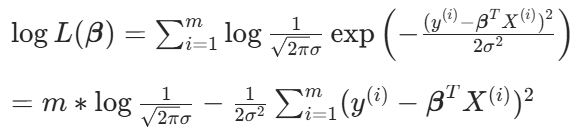
误差项分析
观察一下最终计算结果:
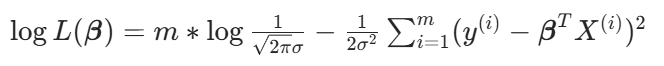
目标函数:
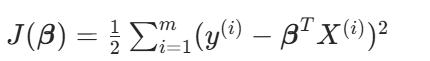
求式子=0的极小值
最小二乘法求解
目标函数:
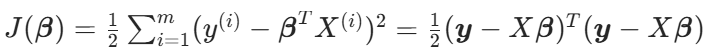
求导结果:
![]()
偏导等于 0:
![]()





深度解析:从标准架构到商用实践)




)





 理论知识)

)
