当使用定焦镜头时，仍然可以调整镜头与感光元件（或胶片）之间的距离时，使得不同距离的物体在感光元件上形成清晰的影像。对此可以用高斯透镜公式进行解释：

一、透镜成像的基本原理

在光学中，一个基本的公式是：

$$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$$

其中：

• $f$：镜头的焦距（焦距是镜头本身的属性，固定不变）
• $u$：物距，即被摄物体到镜头的距离
• $v$：像距，即镜头到感光元件（如相机传感器）的距离

这个公式叫做高斯透镜公式，它描述了光线通过镜头后在感光元件上成像的条件。

---

二、高斯透镜公式推导

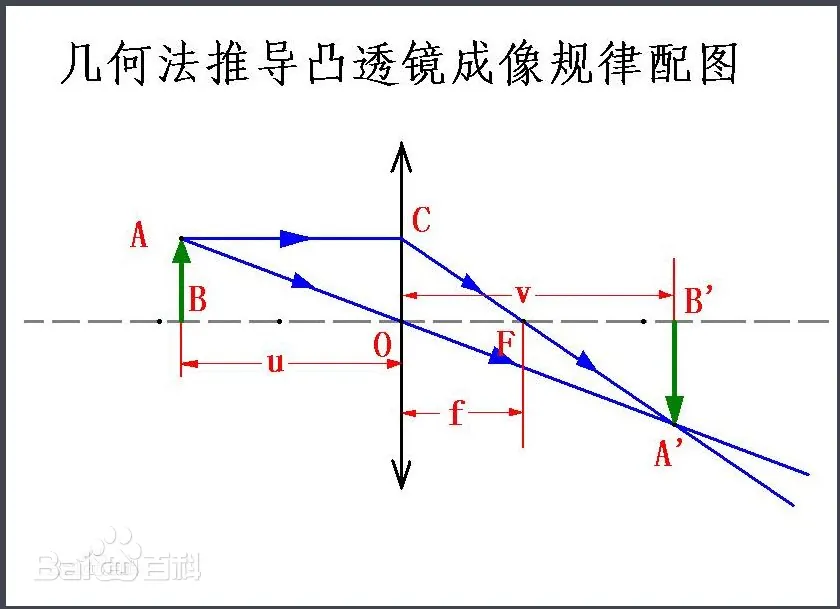
推导步骤

1. 相似三角形关系：

   • 假设有一个物体通过薄透镜成像。根据图像，我们有两对相似三角形：△ABO∽△A’B’O 和 △COF∽△A’B’F。
   • 从 △ABO∽△A’B’O 得到的比例关系为：$$\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{u}{v}$$
   • 从 △COF∽△A’B’F 得到的比例关系为：$$\frac{CO}{A^{\prime }{B}^{\prime }}=\frac{f}{v-f}$$

2. 矩形性质的应用：

   • 因为四边形 ABOC 是一个矩形，所以有 ( AB = CO )。

3. 等式转换：

   • 由上述两点可以知道：$$\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{CO}{A^{\prime }{B}^{\prime }}=\frac{f}{v-f}$$
   • 将$\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{u}{v}$代入上式得：$$\frac{u}{v}=\frac{f}{v-f}$$

4. 交叉相乘并简化：

   • 交叉相乘后得到：$u(v-f)=vf$
   • 展开并重新排列得到：$uv-uf=vf$

5. 移项与除法操作：

   • 由于 $uvf\ne 0$，我们可以两边同时除以 $uvf$ 来得到更简洁的形式：
     $$\frac{uv}{uvf}-\frac{uf}{uvf}=\frac{vf}{uvf}$$
   • 简化上述表达式可得：$$\frac{1}{f}-\frac{1}{v}=\frac{1}{u}$$

6. 最终形式：

   • 最后将方程调整为标准形式：$$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$$

三、高斯透镜公式跟针孔模型的关系

针孔相机模型

针孔相机模型是一种理想化的几何模型，它假设光线通过一个无穷小的孔（针孔）进入相机并在对面的平面上形成倒立的实像。在针孔模型中，并没有使用透镜来聚焦光线，因此不存在焦距的概念（即没有(f)）。在这个模型下，图像平面的位置相对于针孔的距离是一个固定的参数，通常称为“焦距”以方便描述，但它与光学透镜中的焦距概念不同。针孔模型主要用于简化场景理解、3D 重建等任务中的数学计算，尤其是在不需要考虑镜头畸变的情况下。

高斯透镜公式

另一方面，高斯透镜公式适用于带有透镜系统的相机，其中涉及到物距(u)、像距(v)和透镜焦距(f)之间的关系。这个公式描述了如何根据物体距离调整像距（或反之），以便在感光元件上获得清晰的影像。

二者关系

当使用针孔模型进行相机标定时，实际上是在利用一种简化的数学模型来近似真实世界的成像过程。在这种情况下，“焦距”指的是从针孔到图像传感器的距离，这与透镜系统中的焦距概念并不直接对应。因此，在针孔相机模型中，传感器位置固定地放置在所谓的“焦距”处，并不意味着违反了高斯透镜公式；这是因为两者基于完全不同的物理基础——一个是无透镜的理想化情况，另一个则是基于实际透镜的光学性质。

总结来说，针孔相机模型和应用高斯透镜公式的透镜成像模型是两个独立的概念。针孔模型用于简化成像过程，而高斯透镜公式则精确描述了包含透镜的成像系统的行为。将针孔模型应用于相机标定时，实际上是选择了一种简化的方式来处理成像问题，而不是直接应用或违背了高斯透镜公式。

尽管在名称上针孔相机的“焦距”和高斯透镜中的像距都使用了(f)这一符号，但它们代表的意义并不完全相同：

• 针孔相机模型中的“焦距”(f)是一个固定值，它定义了针孔到成像平面的距离，且不涉及光学聚焦的概念。
• 而高斯透镜公式中的像距(v)则依赖于具体的光学设置，包括物距(u)和透镜的物理特性（即焦距，并且可以通过调整这些参数来获得不同的成像效果。

针孔模型的f更偏向于高斯透镜公式里的v

1. 针孔模型与像距

• 在针孔相机模型中，所谓的“焦距”(f)实际上是指从针孔到成像平面（传感器或胶片）的距离。这个距离决定了图像的大小和视角。
• 当针孔相机的“焦距”(f)增加时，相当于增大了像距(v)，这会导致视场变窄，物体在成像平面上的投影变小；反之，当“焦距”减小时，视场变宽，物体的投影变大。

2. 高斯透镜公式中的像距(v)

• 通过调整镜头的位置可以使得像距(v)发生变化，从而让不同距离上的物体能够在感光元件上形成清晰的影像。