说明

如果已经有一个GitHub账号，这是一个很好的起点！版本控制是一个帮助你管理代码或其他文件变化的工具，就像给你的项目加了一个“时间机器”，可以随时回溯历史、协作编辑，而不会乱套。下面我将从基础开始，层层展开说明。整个内容分为几个部分：介绍、原理、用途、操作说明、步骤、流程图和关系图。我会用简单语言，避免专业术语，如果用到会解释清楚。每个部分用小标题分隔，内部用编号或 bullet point 列表，便于阅读。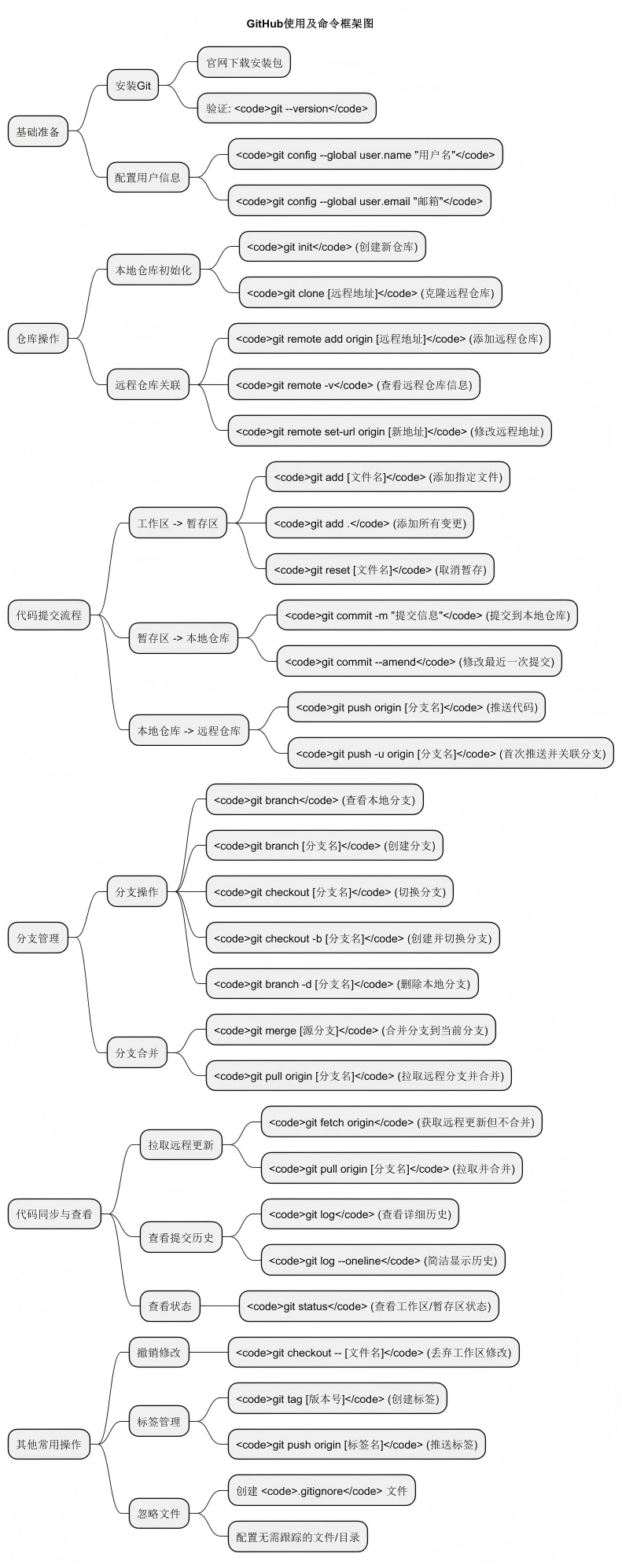

1. 版本控制的介绍版本控制（Version Control），也叫源代码管理（Source Control）。

是一种跟踪和管理文件变化的系统。它最常用在软件开发中，但也可以用于文档、设计图等任何需要多次修改的文件。

• 简单比喻：想象你写一篇文章，先写初稿（版本1），然后修改添加内容（版本2），如果改错了，想回到版本1？没有版本控制，你可能需要手动复制文件备份。有了版本控制，它自动记录每个变化，就像日记本，你可以随时“翻页”回去。
• 常见工具：最流行的是Git（一个免费开源的版本控制系统），GitHub是基于Git的在线平台，用于存储和分享项目（你已经有账号了）。
• 为什么适合小白：Git一开始可能觉得复杂，但学会基本命令后，就像用Word的“保存”和“撤销”一样简单。GitHub提供图形界面（网页），减少命令行操作。

版本控制不是编程语言，而是工具，帮助你组织工作。