机器学习-决策树（DecisionTree）

在这里插入图片描述

0 回归决策树展示

import pandas as pd
import numpy as np 
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import root_mean_squared_error, r2_score
from sklearn.model_selection import GridSearchCV,KFold
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
data =pd.read_csv("../data/house-prices-advanced-regression-techniques/train.csv")
# 去空
# FireplaceQu表示壁炉质量,空值代表没有壁炉，将空值设置为No Fireplace即可，不必删除
for i in ["Alley","PoolQC","Fence","MiscVal","MiscFeature","MasVnrType","FireplaceQu","BsmtQual","BsmtCond","BsmtExposure","BsmtFinType1","BsmtFinType2","GarageType","GarageFinish","GarageQual","GarageCond","GarageYrBlt"]:data[i]=data[i].fillna(f"no{i}")
# data.isna().any()
data["LotFrontage"]=data["LotFrontage"].fillna(data["LotFrontage"].mean())
# Electrical还有一个空值，直接删除
data.dropna(inplace=True)X = data.drop(columns="SalePrice")
y = data["SalePrice"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)transformer = DictVectorizer()
X_train = transformer.fit_transform(X_train.to_dict(orient="records"))
X_test =transformer.transform(X_test.to_dict(orient = "records"))
# 
X_train = pd.DataFrame(X_train.toarray(),columns=transformer.get_feature_names_out())
X_test = pd.DataFrame(X_test.toarray(),columns=transformer.get_feature_names_out())
#%%estimator = DecisionTreeRegressor( )
cv = KFold(n_splits=5)
estimator =GridSearchCV(estimator,param_grid={'max_depth': [2,5,10,15,20,30],"min_samples_split":[3,5,7,10,15,20],"min_samples_leaf":[1,3,5,7,10,15,20,30],
},scoring='neg_mean_squared_error',cv=cv,n_jobs=-1)#设负均方误差为目标estimator.fit(X_train,y_train)print("best_params_",estimator.best_params_)
print("best_score_",estimator.best_score_)
y_pred = estimator.best_estimator_.predict(X_test)
y_pred_train = estimator.best_estimator_.predict(X_train)print(f"Root Mean Squared Error: {root_mean_squared_error(y_test,y_pred)}")# 重要性评估
# 构建特征重要性表
importances = pd.DataFrame({"feature": X_train.columns,"importance": estimator.best_estimator_.feature_importances_
})# 按重要性降序排序
importances = importances.sort_values(by="importance", ascending=False)
print(importances)

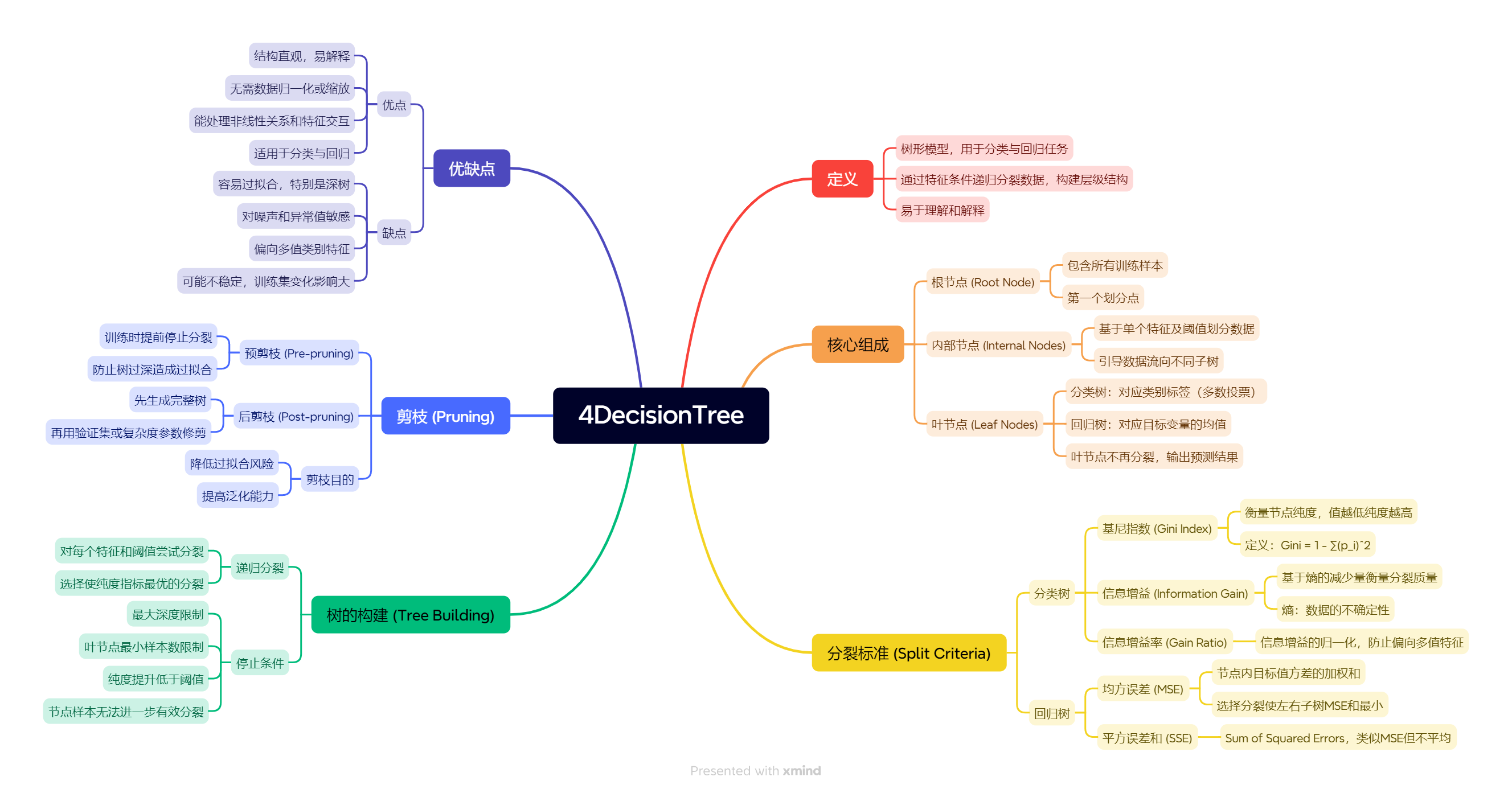
1 相关知识

(信息熵和基尼指数的公式都是构造出来的，根据现有的理论用创造一个满足所有理论因素的公式来描述)

1.1 信息熵

信息熵（Information Entropy）用来衡量信息的不确定性或随机性程度。

定义

对于一个离散随机变量 $X$ ，其可能取值为 ${x_1, x_2, ..., x_n\}$ ，对应的概率分布为 ${p_1, p_2, ..., p_n\}$ ，则信息熵定义为：
$-\sum_{i=1}^{n} p_i \log_2 p_i$
其中， $p_i = P(X = x_i)$ 表示随机变量 $X$ 取值为 $x_i$ 的概率。

物理意义

信息熵反映了系统的不确定性：

熵值越大，系统越混乱，不确定性越高
熵值越小，系统越有序，不确定性越低
当系统完全确定时，熵为0

1.2 条件信息熵

条件信息熵（Conditional Information Entropy）表示在已知随机变量 $Y$ 的条件下，随机变量 $X$ 的不确定性。

定义

给定随机变量 $X$ 和 $Y$ ， $X$ 在 $Y$ 条件下的条件熵定义为：
$\sum_{j} P(Y = y_j) H(X|Y = y_j)$
$-\sum_{j} P(Y = y_j) \sum_{i} P(X = x_i|Y = y_j) \log_2 P(X = x_i|Y = y_j)$
$-\sum_{i,j} P(X = x_i, Y = y_j) \log_2 P(X = x_i|Y = y_j)$

1.3 信息增益

信息增益（Information Gain）是机器学习中特征选择的重要指标，特别是在决策树算法中广泛应用。

定义

信息增益定义为原始信息熵与条件信息熵的差值：
$I G (X, Y) = H (X) - H (X ∣ Y)$
也可以表示为：
$I G (X, Y) = H (Y) - H (Y ∣ X)$

1.4信息增益比

为了避免信息增益偏向于取值较多的特征，引入信息增益比（Gain Ratio）：

$\frac{IG(X, Y)}{H(Y)}$

信息增益比通过除以特征的固有值来标准化信息增益，使得特征选择更加公平。

1.5 基尼指数

基尼指数（Gini Index）是另一种衡量数据集纯度的指标，广泛应用于决策树算法中，特别是CART（Classification and Regression Tree）算法。

定义

对于包含 $k$ 个类别的数据集 $D$ ，基尼指数定义为：
$\sum_{i=1}^{k} p_i^2$
其中， $p_i$ 表示数据集 $D$ 中第 $i$ 类样本所占的比例。

1.6 条件基尼指数

当根据特征 $A$ 将数据集 $D$ 划分为多个子集时，条件基尼指数定义为：
$\sum_{v=1}^{V} \frac{|D^v|}{|D|} Gini(D^v)$
其中：

$V$ 是特征 $A$ 的可能取值数量
$D^v$ 表示特征 $A$ 取值为 $v$ 的样本子集
$D^v|$ 和 $∣ D ∣$ 分别表示子集和原数据集的样本数量

1.7基尼增益

基尼增益定义为原始基尼指数与条件基尼指数的差值：
$Gini\_Gain(D, A) = Gini(D) - Gini(D, A)$

1.7 基尼指数与信息熵的关系

基尼指数和信息熵都用于衡量数据集的不纯度，它们具有相似的性质：

两者都在数据集完全纯净时达到最小值0
两者都在各类样本均匀分布时达到最大值
在二分类问题中： $\approx 2p(1-p)$ ， $H(D) = -p\log_2 p - (1-p)\log_2(1-p)$

2决策树

2.1 决策树

1> 是一种树形结构，本质是一颗由多个判断节点组成的树
2> 其中每个内部节点表示一个属性上的判断，
3> 每个分支代表一个判断结果的输出，
4> 最后每个叶节点代表一种分类结果。

2.2 决策树的优化：

决策树学习旨在构建一个与训练数据拟合很好，并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题(NP完全问题目前无法通过确定性算法直接求解，只能通过启发式函数(如信息熵、信息增益)逼近解，)。

决策树学习算法包括3部分：特征选择、树的生成和树的剪枝。常用的算法有ID3、C4.5和CART。

2.3 决策树特征选择的准则

1】样本集合 $D$ 对特征 $A$ 的信息增益（ID3）

$g (D, A) = H (D) - H (D ∣ A)$

$H(D)=−∑k=1K∣Ck∣∣D∣log⁡2∣Ck∣∣D∣H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|}$

$A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)$

其中， $H (D)$ 是数据集 $D$ 的熵， $H(D_i)$ 是数据集 $D_i$ 的熵， $H (D ∣ A)$ 是数据集 $D$ 对特征 $A$ 的条件熵。 $D_i$ 是 $D$ 中特征 $A$ 取第 $i$ 个值的样本子集， $C_k$ 是 $D$ 中属于第 $k$ 类的样本子集。 $n$ 是特征 $A$ 取值的个数， $K$ 是类的个数。

2】样本集合 $D$ 对特征 $A$ 的信息增益比（C4.5）

通过计算信息增益率，我们可以确保选择的特征不仅能提供较大的信息增益，还能避免过于依赖那些取值较多、看似“更复杂”的特征。

$gR(D,A)=g(D,A)H(D)g_{R}(D, A)=\frac{g(D, A)}{H(D)}$

其中， $g (D, A)$ 是信息增益， $H (D)$ 是数据集 $D$ 的熵。

3】样本集合 $D$ 的基尼指数（CART）

(相比信息熵的优势：计算简单、数值稳定)
$Gini⁡(D)=1−∑k=1K(∣Ck∣∣D∣)2\operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}$

特征 $A$ 条件下集合 $D$ 的基尼指数：

$Gini⁡(D,A)=∣D1∣∣D∣Gini⁡(D1)+∣D2∣∣D∣Gini⁡(D2)\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)$

3 决策树构建

计算y的信息熵(gini指数),然后对每个特征的每个类别进行划分，比如选类别1，类别1有A/B，计算出选A的概率×A行的信息熵/gini+B的概率何B行的信息熵/gini(这就是划分后的信息熵/gini)，最后算出信息增益、信息增益比或者gini增益，最大的作为第一个决策树节点，然后若信息熵仍不为0，继续选择下一个节点，若为零，则分出一个分支通向分类结果。循环这个过程直到叶子节点的信息熵全为0，皆为分类结果，至此完成决策树构建。

注意点：
1 对于连续的特征决策树对连续特征就是“把所有取值排序，检查每两个相邻值的中点，挑一个让不纯度下降最大的作为阈值”， “分位数近似”只检查若干分位点而非所有两个相邻值的中点。
2 由于树的分裂与否是自己和自己对比，不需要和别的特征交互，故天然不需要同度量化

4 决策树的剪枝：

由于生成的决策树存在过拟合问题，需要对它进行剪枝，以简化学到的决策树。决策树的剪枝，往往从已生成的树上剪掉一些叶结点或叶结点以上的子树，并将其父结点或根结点作为新的叶结点，从而简化生成的决策树。

4.1预剪枝

预剪枝是在构建决策树时，在节点进行分裂前，根据一些预定义的条件来决定是否继续分裂。Scikit - learn中提供了一些参数来实现预剪枝：
max_depth：用于设置决策树的最大深度。如果树的深度达到或超过此值，节点将不再分裂。
min_samples_split：用于设置进行分裂所需的最小样本数。如果节点中的样本数少于此值，节点将不再分裂。
min_samples_leaf：用于设置叶节点中的最小样本数。如果叶节点中的样本数少于此值，则不会继续分裂

4.2 后剪枝

常见的后剪枝标准/方法

1 误差估计剪枝（Error-based Pruning）
典型代表：C4.5 使用的基于置信区间的错误率估计。
思路：用统计方法估计子树和剪枝后叶子节点的分类误差，剪掉对泛化误差无益的子树。
利用二项分布的置信区间计算误差上界。

2 代价复杂度剪枝（Cost-Complexity Pruning）
典型代表：CART 算法采用的剪枝方式。
公式：
$R_α(T) = R(T) + α |T|$
其中 R(T) 是树 T 的误差率，|T| 是叶节点数，α 是复杂度惩罚系数。
通过调整 α 权衡树的复杂度和误差，选择最优子树。
一般使用交叉验证选择 α。

3 最小误差剪枝（Minimal Error Pruning）
直接比较剪枝前后在验证集上的误差率。
如果剪枝后误差不增大，则进行剪枝。

4 统计检验剪枝
用统计检验（如卡方检验）判断节点分裂是否显著，不显著则剪枝。

5 ID3、C4.5、CART算法的差别

对比维度	ID3	C4.5	CART	改进意义
特征选择指标	信息增益（Information Gain）	信息增益率（Gain Ratio）	分类：基尼指数（Gini Index）回归：最小平方误差（MSE）	解决 ID3 偏向取值多特征(比如极端情况特征分类为一行一类，那每一类都是纯的，但是分类没有意义)的问题，CART 则统一了分类和回归的处理方式
特征类型支持	仅支持离散特征	支持离散特征和连续特征	支持离散特征和连续特征	扩展到数值型特征，提高算法适用性
缺失值处理	不支持	支持（概率权重分配样本到分支）	支持（替代变量或加权处理）	减少因缺失值导致的数据丢失
树结构	多叉树	多叉树	二叉树	CART 的二叉划分便于剪枝和计算
剪枝策略	无剪枝（易过拟合）	后剪枝（基于置信区间错误率）	代价复杂度剪枝（Cost-Complexity Pruning）	提高泛化能力，减少过拟合
输出结果	类别标签	类别标签或类别概率分布	分类标签/概率或回归预测值	输出概率/连续值提升灵活性
对噪声和异常值的鲁棒性	较差	较好	较好	剪枝和连续值处理提升了抗噪性
适用任务	分类	分类	分类 + 回归	CART 能用于回归，应用范围更广
泛化能力	较弱	较强	较强	改进后模型更适应新数据

6 决策树算法api

class sklearn.tree.DecisionTreeClassifier(criterion=“gini”,
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
random_state=None)

参数：
1】criterion：特征选择标准
“gini”
或者
“entropy”，前者代表基尼系数，后者代表信息增益。⼀默认
“gini”，即CART算法。
2】min_samples_split：内部节点再划分所需最⼩样本数
这个值限制了⼦树继续划分的条件，如果某节点的样本数少于min_samples_split，
则不会继续再尝试选择最优特征来进⾏划分。
默认是2.如果样本量不⼤，不需要管这个值。
如果样本量数量级⾮常⼤，则推荐增⼤这个值。
⼀个项⽬例⼦，有⼤概10万样本，建⽴决策树时，选择了min_samples_split = 10。
可以作为参考。
3】min_samples_leaf：叶⼦节点最少样本数
这个值限制了叶⼦节点最少的样本数，如果某叶⼦节点数⽬⼩于样本数，
则会和兄弟节点⼀起被剪枝。
默认是1, 可以输⼊最少的样本数的整数，或者最少样本数占样本总数的百分⽐。
如果样本量不⼤，不需要管这个值。如果样本量数量级⾮常⼤，则推荐增⼤这个值。
之前的10万样本项⽬使⽤min_samples_leaf的值为5，仅供参考。
4】max_depth：决策树最⼤深度
决策树的最⼤深度，默认可以不输⼊
如果不输⼊的话，决策树在建⽴⼦树的时候不会限制⼦树的深度。
⼀般来说，数据少或者特征少的时候可以不管这个值。
如果模型样本量多，特征也多的情况下，推荐限制这个最⼤深度，具体的取值取决于数据的分布。
常⽤的可以取值10 - 100
之间

5】random_state：随机数种⼦

6.1 决策树分类


from sklearn.tree import DecisionTreeClassifier
import pandas as pd
data = pd.read_csv('../pandasPD/data/titanic/train.csv')
X = data[["Sex", "Age", "Sex"]]
y = data["Survived"]
X.loc[:, "Age"] = X.loc[:, "Age"].fillna(X.loc[:, "Age"].median())  # 去空
#%%
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
#%%
from sklearn.feature_extraction import DictVectorizer
transfer = DictVectorizer()
X_train = transfer.fit_transform(X_train.to_dict(orient='records'))  # orient='records'将每一行数据转换成一个字典
X_test = transfer.transform(X_test.to_dict(orient='records'))  # orient='records'将每一行数据转换成一个字典
# 查看结果
pd.DataFrame(X_train.toarray(), columns=transfer.get_feature_names_out())
# 不需要特征缩放
#%%
# 训练
estimator = DecisionTreeClassifier(# max_depth=5
)
estimator.fit(X_train, y_train)
#%%
from sklearn.metrics import accuracy_score, recall_score, f1_score, classification_report
# 评估
y_pred = estimator.predict(X_test)
ret = estimator.score(X_test, y_test)
print(f"准确率：{ret}")
print(f"精确度：{accuracy_score(y_test, y_pred)}")

6.2 回归决策树

关键特点：

可解释性强：决策路径像流程图一样清晰
自动特征选择：会优先用最有区分度的特征（比如先问犬种再问年龄）
不需要特征缩放：对身高(cm)和体重(kg)这种混合单位很友好

注意：

容易过拟合（解决方法：限制树深度/设置最小样本量）
对异常值敏感（比如遇到200斤的超级胖柯基）
预测值是阶梯状的（无法输出连续曲线）

叶节点（Leaf Node）
回归树中的叶节点表示最终的预测区域，每个叶节点对应训练数据的一个子集。叶节点的预测值为该节点中所有训练样本目标值的均值。
(换句话说就是每个训练样本最后都会进入某个叶子节点，这个叶子节点的值就取决于那些进入这个叶子节点的样本的平均值)

纯度指标（Purity Measure）
回归树通过最小化叶节点内目标值的**均方误差（MSE）**来衡量纯度，分裂时选择使得加权子节点MSE和最小的特征及阈值。

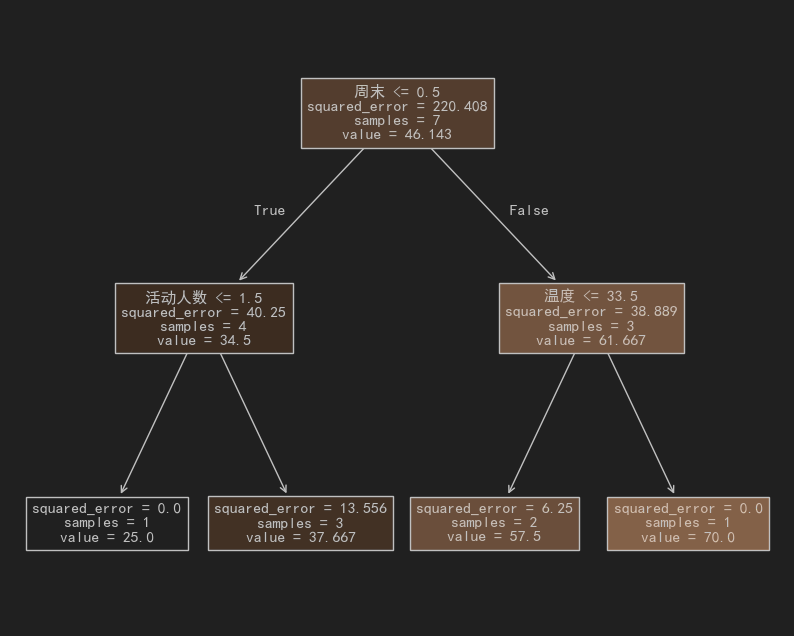
import numpy as np
from sklearn.tree import DecisionTreeRegressor,plot_tree
from sklearn.metrics import root_mean_squared_error, r2_score
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 假如有7天的销售数据  特征：
# 天气温度
# 是否周末（1是 0否）
# 附件的活动人数# 标签（目标）：
# 卖出的冰淇淋 （箱）
new_data = [[28,0,3,42],[32,1,5,60],[25,0,2,38],[30,1,4,55],[22,0,1,25],[35,1,6,70],[26,0,2,33]]
new_data = np.array(new_data)
X =new_data[:,:3] 
y = new_data[:,3]
estimator = DecisionTreeRegressor(max_depth=2,# 树的最大深度min_samples_split=2 , # 节点至少需要两个样本才能分裂min_samples_leaf=1,random_state=42,
)
estimator.fit(X,y)
y_pred = estimator.predict(X)
print(root_mean_squared_error(y,y_pred))
plt.figure(figsize=(10,8))
plot_tree(estimator,feature_names=["温度","周末","活动人数"],filled=True, # 填充颜色    )
plt.show()
new_x = np.array([30,0,5]).reshape(1,-1)
pred=estimator.predict(new_x)
print(pred)