《算法导论》第 21 章-用于不相交集合的数据结构

引言

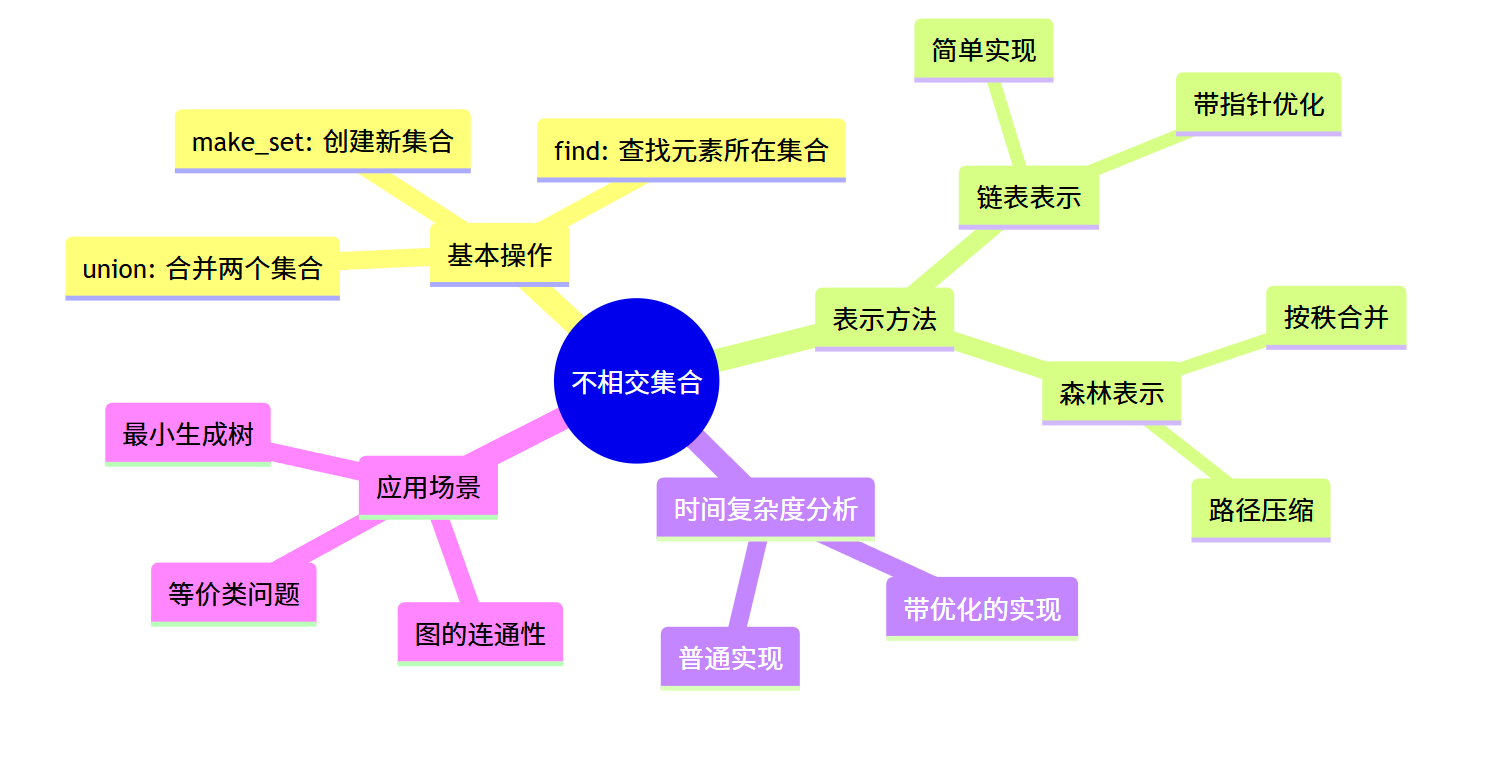
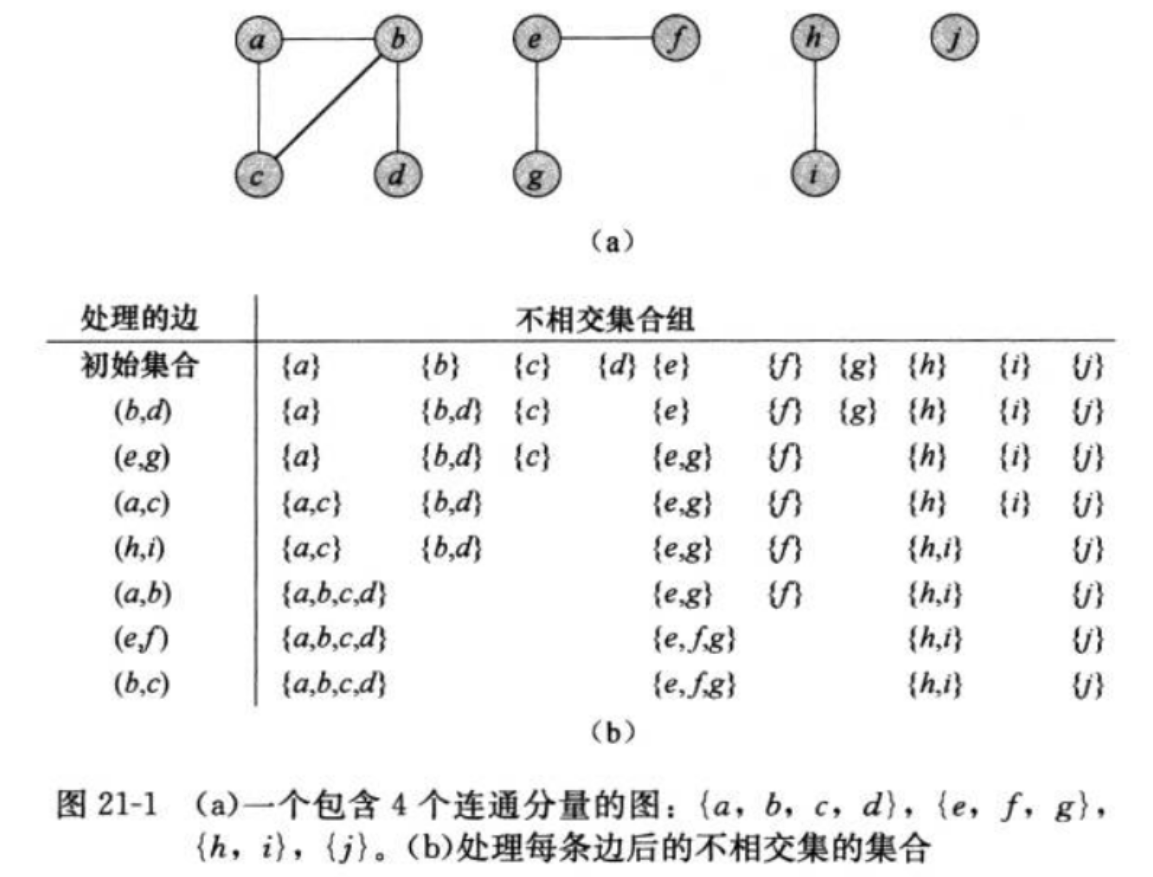
不相交集合（Disjoint Set），也称为并查集（Union-Find），是一种非常实用的数据结构，主要用于处理一些元素分组的问题。它支持高效的集合合并和元素查找操作，在很多算法中都有重要应用，如 Kruskal 最小生成树算法、图的连通性问题、等价关系问题等。

本文将详细讲解《算法导论》第 21 章内容，包括不相交集合的基本操作、两种主要表示方法（链表和森林）以及相关的优化策略，并提供完整可运行的 C++ 代码实现。

思维导图

21.1 不相交集合的操作

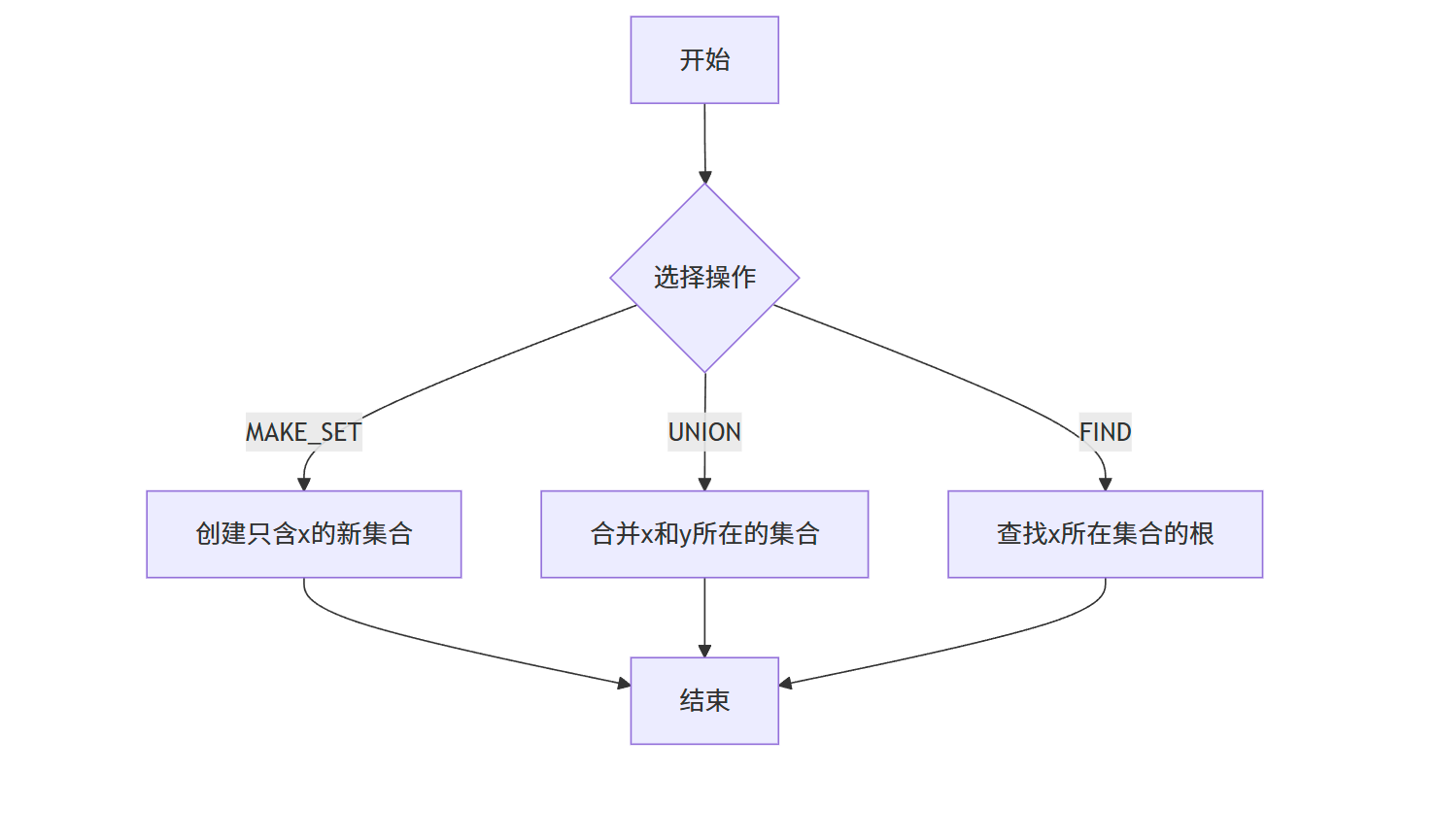
不相交集合数据结构主要支持以下三种操作：

MAKE_SET(x)：创建一个新的集合，其中只包含元素 x，且 x 没有父节点（即自身为根）。
UNION(x, y)：将包含 x 的集合和包含 y 的集合合并成一个新的集合。
FIND(x)：找到包含 x 的集合的根节点，可用于判断两个元素是否属于同一个集合。

操作流程图

应用场景示例

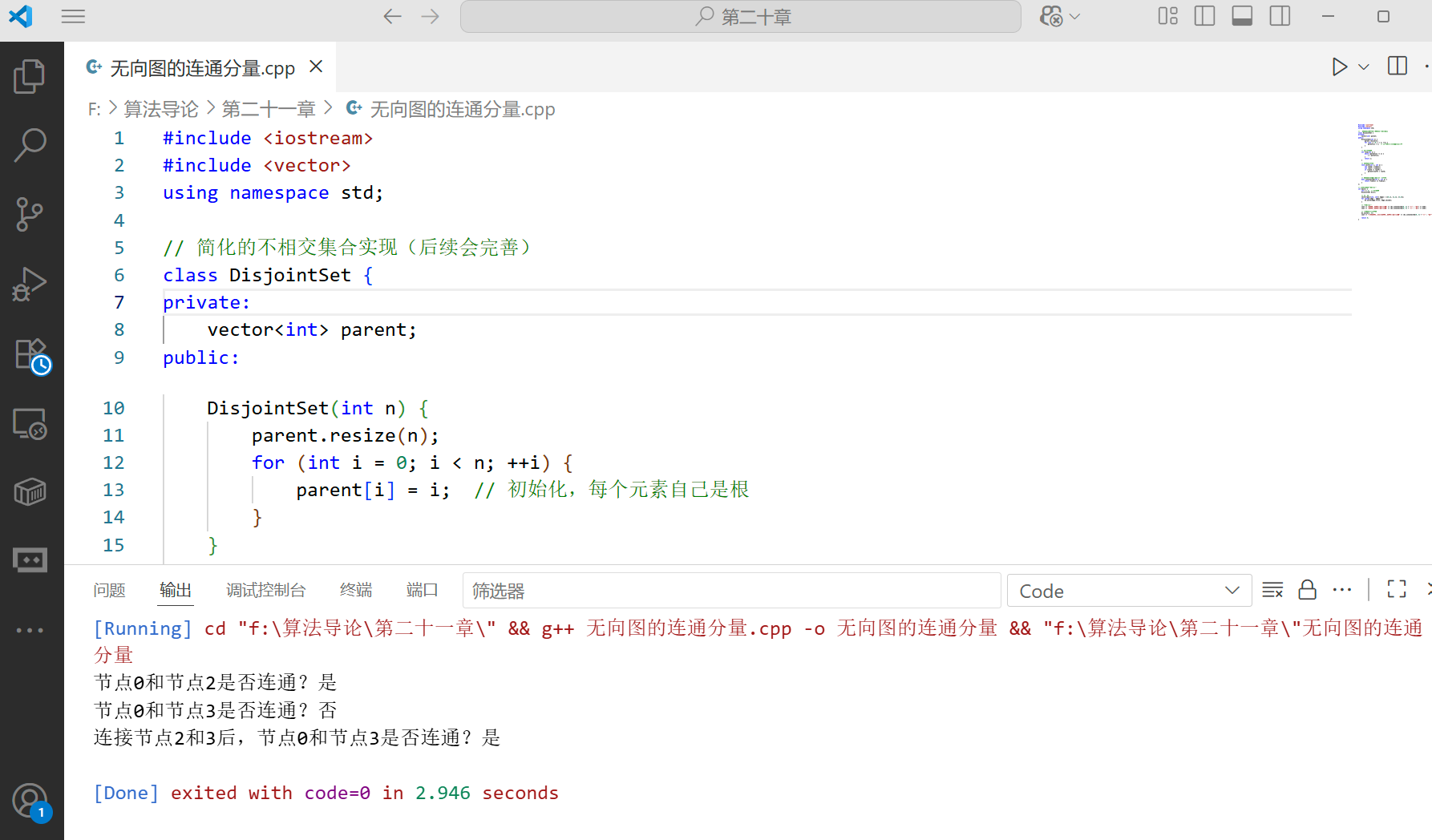
不相交集合最典型的应用之一是判断无向图的连通分量。例如，我们可以用不相交集合来跟踪网络中哪些节点是连通的：

#include <iostream>
#include <vector>
using namespace std;// 简化的不相交集合实现（后续会完善）
class DisjointSet {
private:vector<int> parent;
public:DisjointSet(int n) {parent.resize(n);for (int i = 0; i < n; ++i) {parent[i] = i;  // 初始化，每个元素自己是根}}// 查找根节点int find(int x) {while (parent[x] != x) {x = parent[x];}return x;}// 合并两个集合void unite(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {parent[rootY] = rootX;}}// 判断两个元素是否在同一个集合bool isConnected(int x, int y) {return find(x) == find(y);}
};// 示例：判断图的连通性
int main() {int n = 5;  // 5个节点DisjointSet ds(n);// 添加边vector<pair<int, int>> edges = {{0,1}, {1,2}, {3,4}};for (auto& edge : edges) {ds.unite(edge.first, edge.second);}// 测试连通性cout << "节点0和节点2是否连通？" << (ds.isConnected(0, 2) ? "是" : "否") << endl;cout << "节点0和节点3是否连通？" << (ds.isConnected(0, 3) ? "是" : "否") << endl;// 连接两个连通分量ds.unite(2, 3);cout << "连接节点2和3后，节点0和节点3是否连通？" << (ds.isConnected(0, 3) ? "是" : "否") << endl;return 0;
}

运行结果：

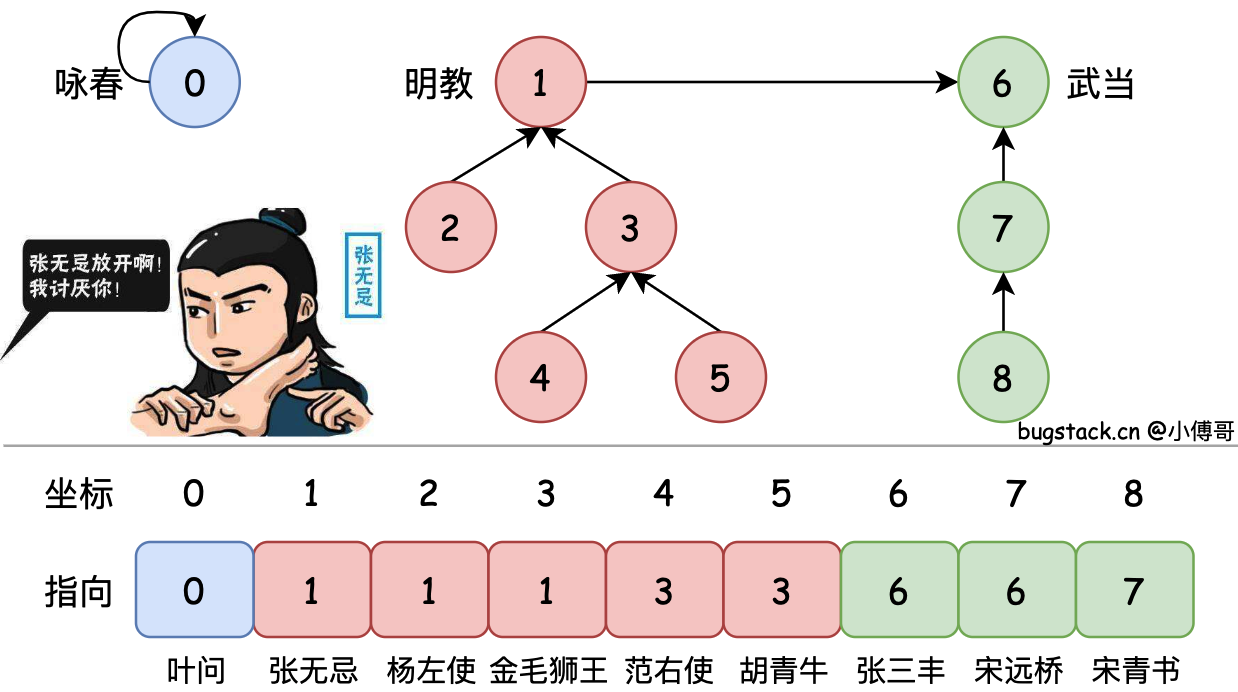
21.2 不相交集合的链表表示

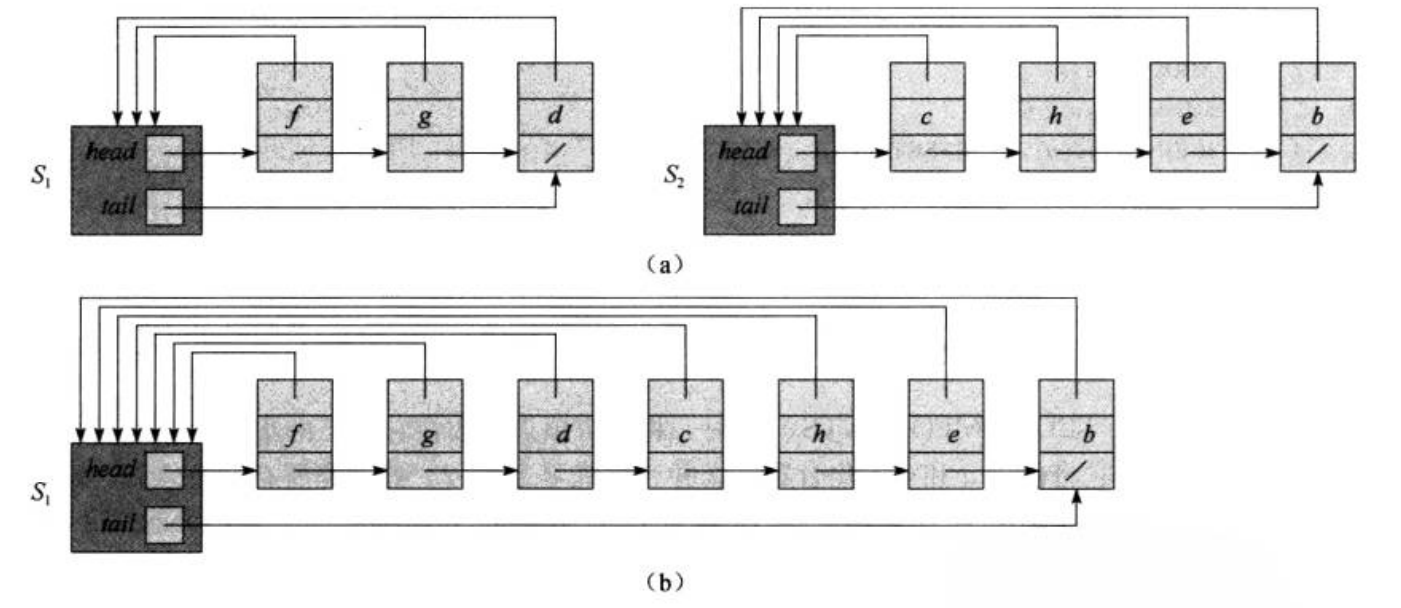
不相交集合的一种简单表示方法是使用链表。每个集合用一个链表表示，每个元素包含一个指向自身的指针、一个指向链表中下一个元素的指针，以及一个指向集合代表（通常是链表的第一个元素）的指针。

链表表示的结构

class Element {- value: int- next: Element- set: Set
}class Set {- head: Element- tail: Element- size: int+ make_set(x): Set+ union_set(x, y): Set+ find_set(x): Element
}Element "n" -- "1" Set : belongs to

链表表示

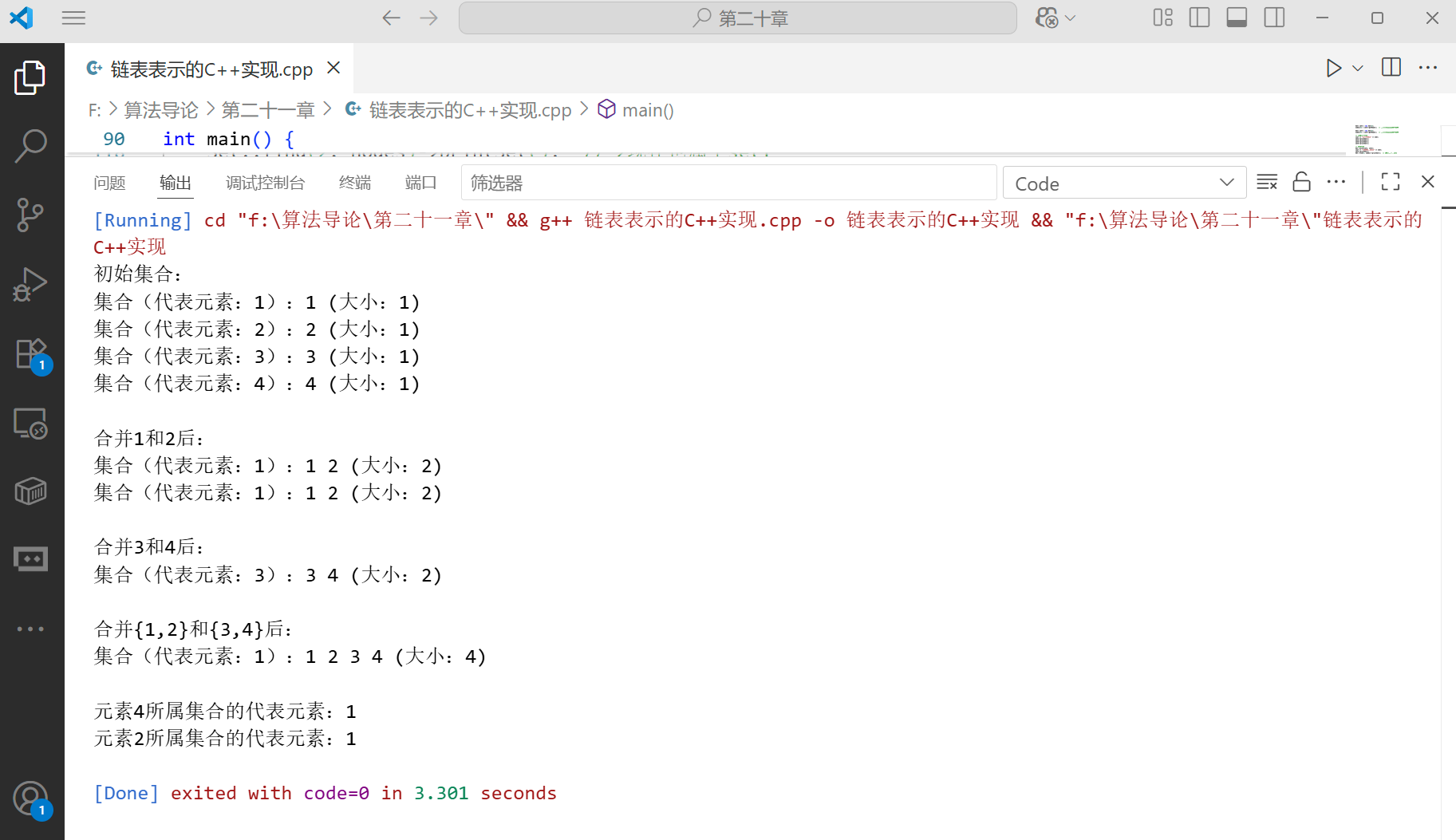
链表表示的 C++ 实现

#include <iostream>
#include <unordered_map>
using namespace std;// 链表节点
struct Node {int value;Node* next;class Set* set;  // 指向所属的集合Node(int val) : value(val), next(nullptr), set(nullptr) {}
};// 不相交集合（链表表示）
class Set {
private:Node* head;  // 集合的头节点（代表元素）Node* tail;  // 集合的尾节点（方便合并操作）int size;    // 集合的大小（用于优化合并）public:// 创建一个只包含val的新集合Set(int val) {head = new Node(val);tail = head;head->set = this;size = 1;}// 添加一个获取头节点的公有方法（解决私有成员访问问题）Node* getHead() const {return head;}// 查找元素val所在的集合static Set* find(int val, unordered_map<int, Node*>& nodes) {if (nodes.find(val) == nodes.end()) {return nullptr;  // 元素不存在}return nodes[val]->set;}// 合并两个集合static void unite(Set* set1, Set* set2) {if (set1 == nullptr || set2 == nullptr || set1 == set2) {return;  // 无效操作或已在同一集合}// 优化：将较小的集合合并到较大的集合中if (set1->size < set2->size) {swap(set1, set2);}// 将set2的元素接到set1的尾部set1->tail->next = set2->head;// 更新set2中所有元素的set指针Node* current = set2->head;while (current != nullptr) {current->set = set1;current = current->next;}// 更新set1的尾部和大小set1->tail = set2->tail;set1->size += set2->size;// 释放set2（可选操作）delete set2;}// 获取集合的代表元素（头节点的值）int getRepresentative() const {return head->value;}// 打印集合中的所有元素void printSet() const {Node* current = head;cout << "集合（代表元素：" << head->value << "）：";while (current != nullptr) {cout << current->value << " ";current = current->next;}cout << "(大小：" << size << ")" << endl;}
};// 示例用法
int main() {// 用于存储所有节点，方便查找unordered_map<int, Node*> nodes;// 创建多个单元素集合Set* set1 = new Set(1);nodes[1] = set1->getHead();  // 使用公有方法获取头节点Set* set2 = new Set(2);nodes[2] = set2->getHead();  // 使用公有方法获取头节点Set* set3 = new Set(3);nodes[3] = set3->getHead();  // 使用公有方法获取头节点Set* set4 = new Set(4);nodes[4] = set4->getHead();  // 使用公有方法获取头节点// 打印初始集合cout << "初始集合：" << endl;set1->printSet();set2->printSet();set3->printSet();set4->printSet();// 合并集合Set::unite(set1, set2);cout << "\n合并1和2后：" << endl;set1->printSet();Set::find(2, nodes)->printSet();  // 2现在也属于set1// 合并更多集合Set::unite(set3, set4);cout << "\n合并3和4后：" << endl;set3->printSet();Set::unite(set1, set3);cout << "\n合并{1,2}和{3,4}后：" << endl;set1->printSet();// 查找元素所属集合cout << "\n元素4所属集合的代表元素：" << Set::find(4, nodes)->getRepresentative() << endl;cout << "元素2所属集合的代表元素：" << Set::find(2, nodes)->getRepresentative() << endl;// 清理内存for (auto& pair : nodes) {delete pair.second;}return 0;
}

运行结果：

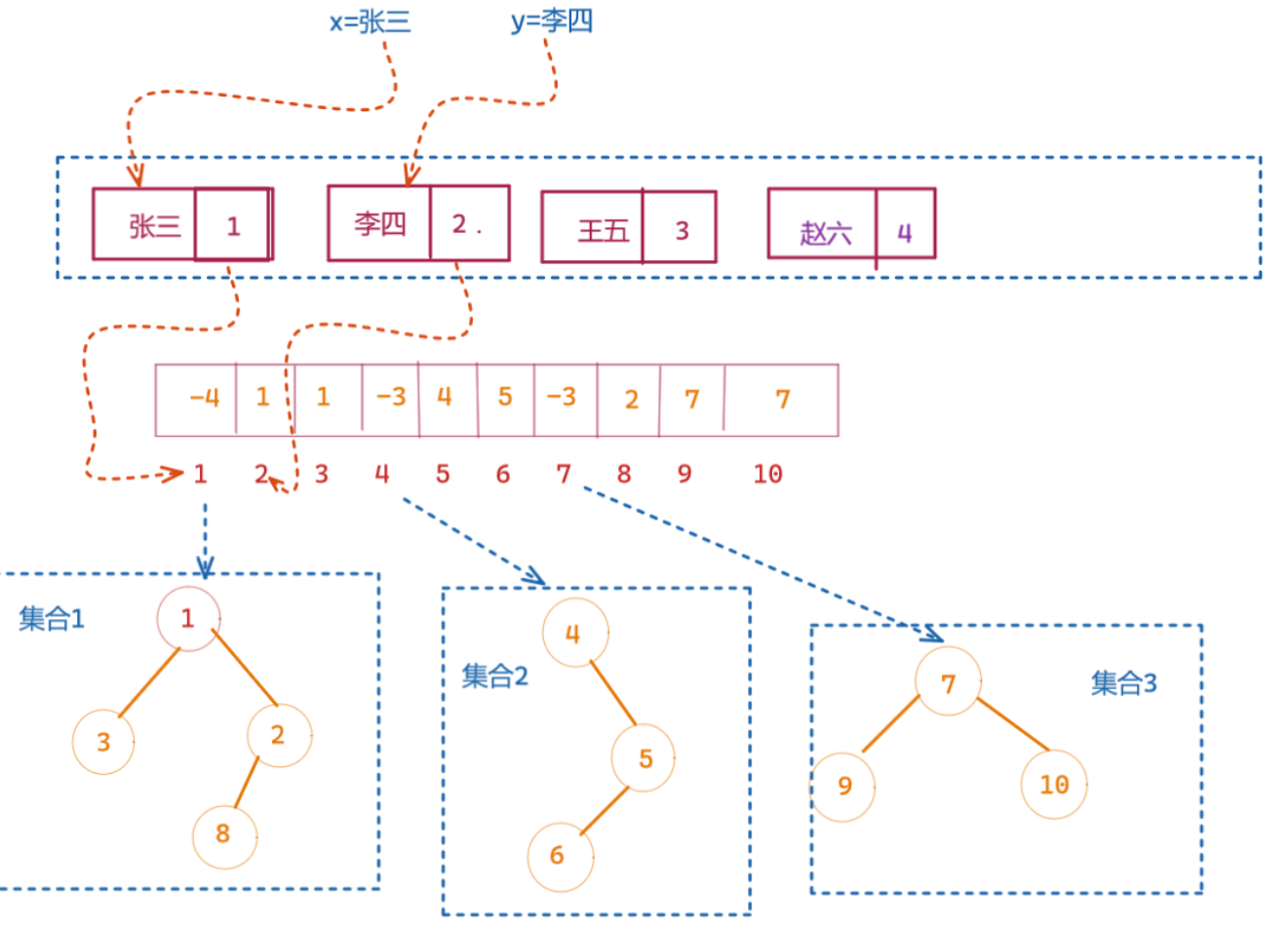
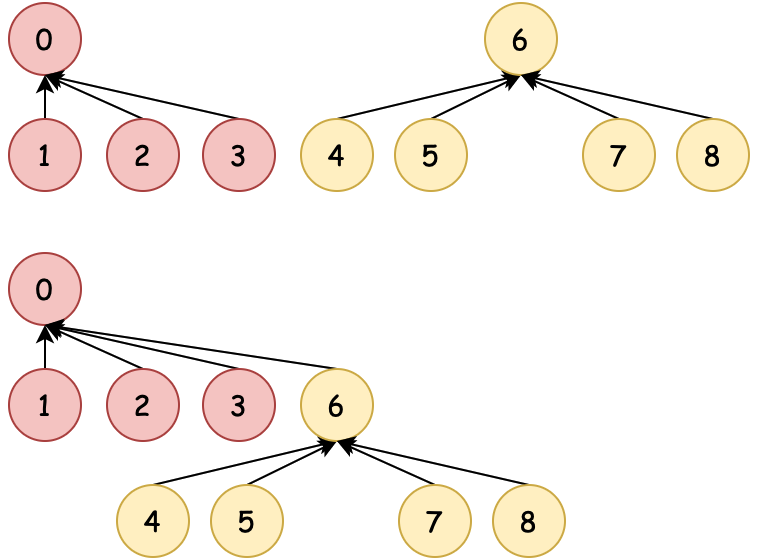
21.3 不相交集合森林

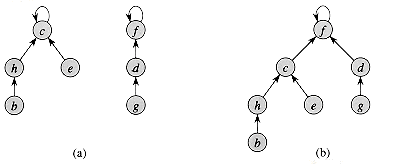
不相交集合的另一种更高效的表示方法是使用森林（一组树）。每个集合用一棵树表示，树中的每个节点都有一个父节点，根节点代表整个集合。

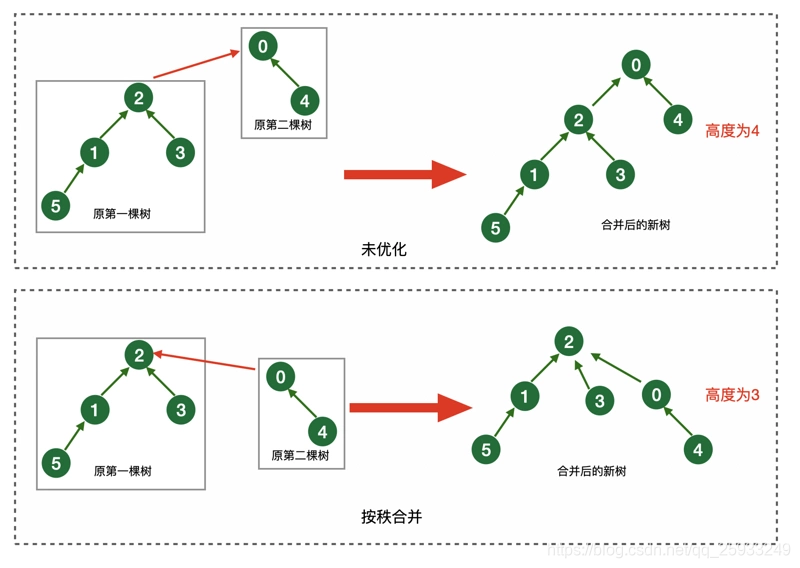
这种表示方法可以通过两种启发式策略进行优化：

按秩合并：总是将秩较小的树合并到秩较大的树中
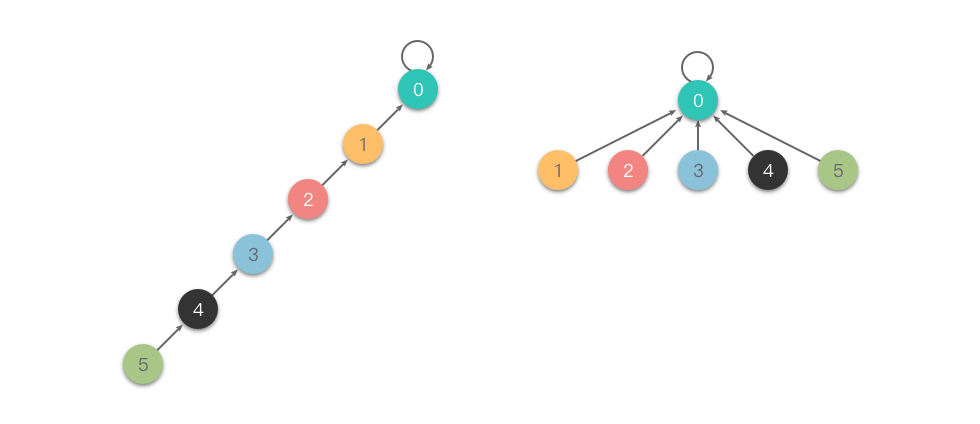
路径压缩：在 find 操作时，将路径上的所有节点直接指向根节点

森林表示的结构

class DisjointSetForest {- parent: array[int]- rank: array[int]+ DisjointSetForest(n: int)+ find(x: int): int+ union(x: int, y: int): void
}

按秩合并流程图

路径压缩流程图

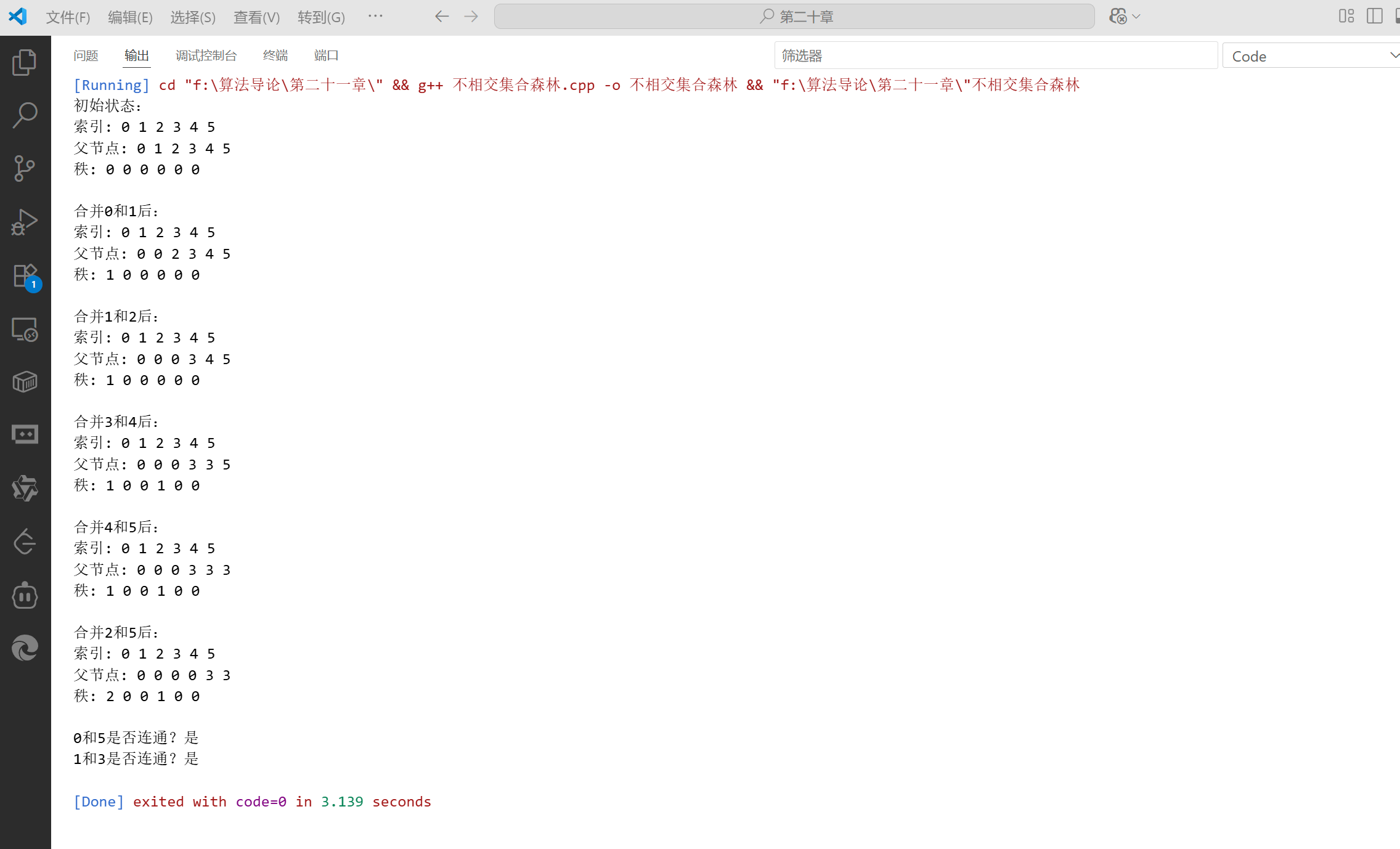
不相交集合森林的 C++ 实现

#include <iostream>
#include <vector>
using namespace std;// 不相交集合森林实现（带路径压缩和按秩合并）
class DisjointSetForest {
private:vector<int> parent;  // 父节点数组vector<int> rank;    // 秩数组（用于按秩合并）public:// 构造函数：初始化n个元素，每个元素自成一个集合DisjointSetForest(int n) {parent.resize(n);rank.resize(n, 0);  // 初始秩都为0for (int i = 0; i < n; ++i) {parent[i] = i;  // 每个元素的父节点是自身}}// 查找x所在集合的根节点（带路径压缩）int find(int x) {// 如果x不是根节点，递归查找其父节点的根，并将x直接指向根节点（路径压缩）if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}// 合并x和y所在的集合（按秩合并）void unite(int x, int y) {int rootX = find(x);  // 找到x的根int rootY = find(y);  // 找到y的根if (rootX == rootY) {return;  // 已经在同一个集合中}// 按秩合并：将秩较小的树合并到秩较大的树中if (rank[rootX] < rank[rootY]) {parent[rootX] = rootY;} else if (rank[rootX] > rank[rootY]) {parent[rootY] = rootX;} else {// 秩相等时，合并后秩加1parent[rootY] = rootX;rank[rootX]++;}}// 判断x和y是否在同一个集合中bool isConnected(int x, int y) {return find(x) == find(y);}// 打印当前的父节点和秩信息（用于调试）void printInfo() {cout << "索引: ";for (int i = 0; i < parent.size(); ++i) {cout << i << " ";}cout << endl;cout << "父节点: ";for (int p : parent) {cout << p << " ";}cout << endl;cout << "秩: ";for (int r : rank) {cout << r << " ";}cout << endl << endl;}
};// 示例：使用不相交集合森林解决连通性问题
int main() {int n = 6;  // 6个元素DisjointSetForest ds(n);cout << "初始状态：" << endl;ds.printInfo();// 执行一些合并操作ds.unite(0, 1);cout << "合并0和1后：" << endl;ds.printInfo();ds.unite(1, 2);cout << "合并1和2后：" << endl;ds.printInfo();ds.unite(3, 4);cout << "合并3和4后：" << endl;ds.printInfo();ds.unite(4, 5);cout << "合并4和5后：" << endl;ds.printInfo();ds.unite(2, 5);cout << "合并2和5后：" << endl;ds.printInfo();// 测试连通性cout << "0和5是否连通？" << (ds.isConnected(0, 5) ? "是" : "否") << endl;cout << "1和3是否连通？" << (ds.isConnected(1, 3) ? "是" : "否") << endl;return 0;
}

运行结果：

*21.4 带路径压缩的按秩合并的分析

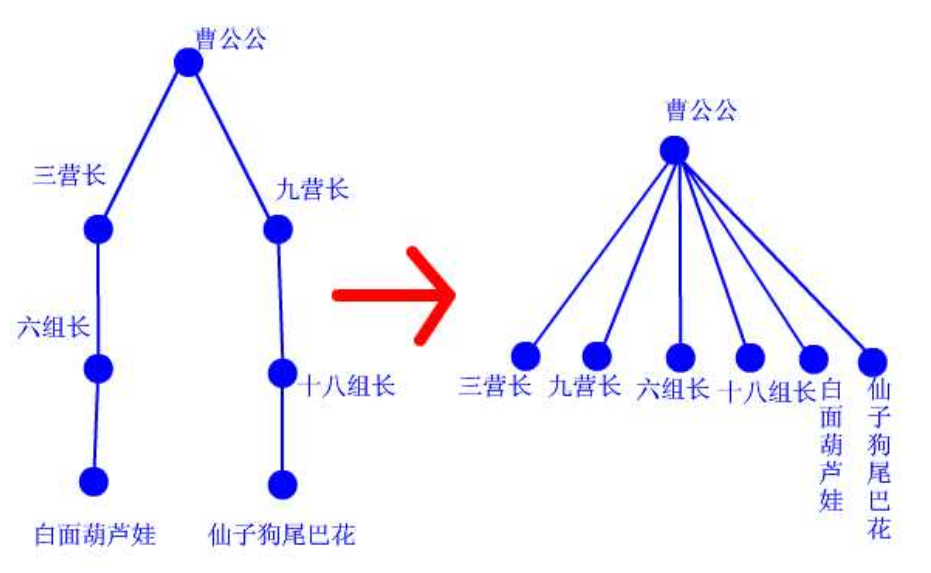
不相交集合森林在使用按秩合并和路径压缩两种优化策略后，其时间复杂度非常接近常数。

具体来说，对于 m 个操作（MAKE_SET、UNION 和 FIND）和 n 个 MAKE_SET 操作，使用带路径压缩的按秩合并的不相交集合森林的时间复杂度为 O (mα(n))，其中 α 是 Ackermann 函数的反函数。

Ackermann 函数定义如下：

A (1, j) = 2^j ，对于 j ≥ 1
A (i, 1) = A (i-1, 2) ，对于 i ≥ 2
A (i, j) = A (i-1, A (i, j-1)) ，对于 i ≥ 2 和 j ≥ 2

反 Ackermann 函数 α(n) 是使得 A (k, k) ≥ n 的最小整数 k。

α(n) 的增长极其缓慢，对于实际应用中可能遇到的所有 n 值（甚至 n 高达 10^600），α(n) 都不会超过 4。因此，在实际应用中，我们可以认为带路径压缩的按秩合并的不相交集合操作是常数时间的。

不同实现的时间复杂度对比

实现方式	查找操作	合并操作	m 个操作的总时间
简单链表（无优化）	O(1)	O(n)	O(mn)
链表（带大小优化）	O(1)	O(log n)	O(m log n)
森林（无优化）	O(n)	O(n)	O(mn)
森林（按秩合并）	O(log n)	O(log n)	O(m log n)
森林（按秩合并 + 路径压缩）	O(α(n))	O(α(n))	O(m α(n))

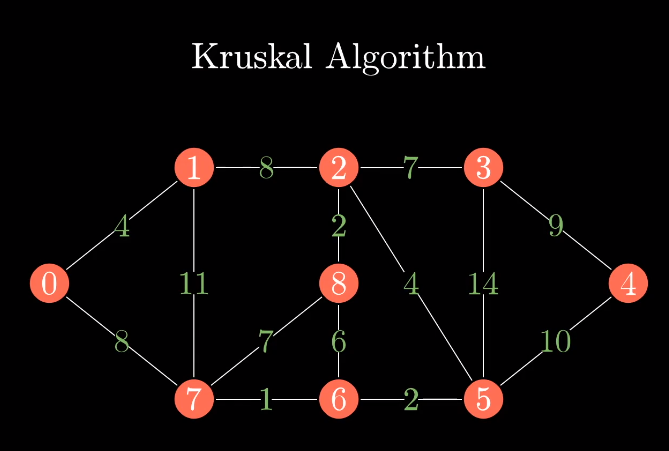
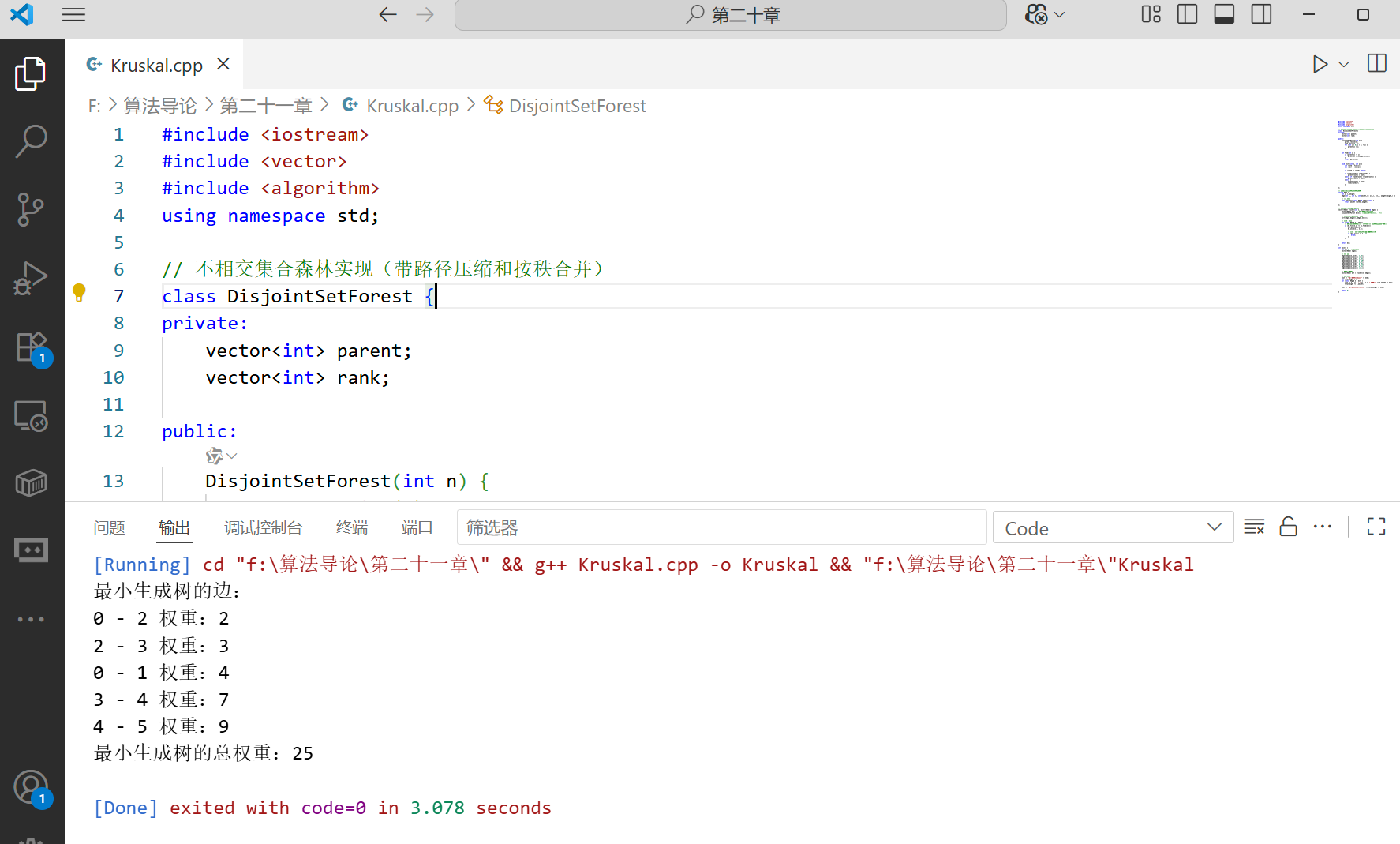
综合案例： Kruskal 算法求最小生成树

Kruskal 算法是一种用于寻找最小生成树的经典算法，它广泛应用了不相交集合数据结构来高效地判断新加入的边是否会形成环。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 不相交集合森林实现（带路径压缩和按秩合并）
class DisjointSetForest {
private:vector<int> parent;vector<int> rank;public:DisjointSetForest(int n) {parent.resize(n);rank.resize(n, 0);for (int i = 0; i < n; ++i) {parent[i] = i;}}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}void unite(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX == rootY) return;if (rank[rootX] < rank[rootY]) {parent[rootX] = rootY;} else if (rank[rootX] > rank[rootY]) {parent[rootY] = rootX;} else {parent[rootY] = rootX;rank[rootX]++;}}
};// 边的结构：起点、终点、权重
struct Edge {int u, v, weight;Edge(int u_, int v_, int weight_) : u(u_), v(v_), weight(weight_) {}// 用于排序bool operator<(const Edge& other) const {return weight < other.weight;}
};// Kruskal算法求最小生成树
vector<Edge> kruskal(int n, vector<Edge>& edges) {vector<Edge> mst;  // 最小生成树的边集合DisjointSetForest ds(n);  // 不相交集合，用于检测环// 按权重从小到大排序所有边sort(edges.begin(), edges.end());// 依次加入边for (const Edge& e : edges) {// 如果两个顶点不在同一个集合中，加入这条边不会形成环if (ds.find(e.u) != ds.find(e.v)) {mst.push_back(e);ds.unite(e.u, e.v);// 当已加入n-1条边时，最小生成树完成if (mst.size() == n - 1) {break;}}}return mst;
}int main() {int n = 6;  // 6个顶点vector<Edge> edges;// 添加边edges.emplace_back(0, 1, 4);edges.emplace_back(0, 2, 2);edges.emplace_back(1, 2, 5);edges.emplace_back(1, 3, 10);edges.emplace_back(2, 3, 3);edges.emplace_back(2, 4, 8);edges.emplace_back(2, 5, 12);edges.emplace_back(3, 4, 7);edges.emplace_back(4, 5, 9);// 求最小生成树vector<Edge> mst = kruskal(n, edges);// 输出结果cout << "最小生成树的边：" << endl;int totalWeight = 0;for (const Edge& e : mst) {cout << e.u << " - " << e.v << " 权重：" << e.weight << endl;totalWeight += e.weight;}cout << "最小生成树的总权重：" << totalWeight << endl;return 0;
}

运行结果：

思考题

实现一个不相交集合数据结构，支持以下操作：
- MAKE_SET (x)：创建一个新集合
- UNION (x, y)：合并两个集合
- FIND (x)：查找元素所在集合
- COUNT (x)：返回 x 所在集合的元素个数
如何使用不相交集合数据结构来解决以下问题：
给定一个包含 n 个元素的数组，以及一系列操作，每个操作是以下两种之一：
- 合并索引 i 和 j 处的元素
- 查询索引 i 和 j 处的元素是否在同一个集合中
  请实现一个高效的数据结构来处理这些操作。
证明：带路径压缩和按秩合并的不相交集合森林的每个 FIND 操作的摊还时间复杂度为 O (α(n))。
设计一个算法，使用不相交集合数据结构来检测一个无向图是否包含环。