这是封面原图，嘿嘿：

二分查找：从基础原理到代码实现

二分查找，这个在算法世界里算不上复杂却总让人在细节上栽跟头的算法，估计不少人都有过类似经历——明明原理一听就懂，上手写却总写出死循环，要么就是边界条件处理得一塌糊涂。但只要真正摸透了它的规律，就会发现它其实是个“只要学会就简单”的典型，今天咱们就借着LeetCode 704.二分查找这道基础题，把它的来龙去脉说清楚。

二分查找的特点

为啥二分查找总让人觉得“看着简单写着难”？

其实核心就是细节太多：
比如这些极易混淆的关键问题，稍不注意就会出错：

• 左边界是left还是left+1？
• 右边界该初始化成nums.size()还是nums.size()-1？
• 循环条件用left < right还是left <= right？

这些小地方一旦疏忽，要么陷入死循环，要么出现漏查元素，甚至引发越界访问，堪称二分查找的“坑点重灾区”。

但它的优点也同样突出，尤其是在效率上的碾压性优势：

• 时间复杂度：O(log n)，对比暴力遍历的O(n)，在数据量大时效率天差地别。

举个直观的例子：
要在100万个元素中查找一个目标数：

• 暴力遍历：最坏情况下需要查100万次；
• 二分查找：最坏情况下仅需20次（因为2^20≈100万）。

这也是二分查找能成为面试高频考点的核心原因。

算法重点

1.原理：不只是“有序”，更是“二段性”

「‼️核心」我们在刚开始接触二分查找的时候经常听说二分查找必须是数组有序的时候才能使用，其实这样说会有些片面，其中本质不是“有序”，而是数组具有 “二段性”
至于什么是二段性简单说就是：能找到一个 “判断条件”，把数组分成两部分 ，一部分一定满足条件，另一部分一定不满足，这样就说这个数组具有二段性

「☝️类比」 比如在书架上找一本《Python编程》，书架是按书名首字母排序的。你随便抽一本中间的书，比如《Java编程》（首字母J），发现它在P的左边，那你就知道《Python编程》一定在右边——这就是生活中的“二段性”。

回到这道题，数组是升序的，“判断条件”就可以是“元素是否小于target”：左边的元素都小于target，右边的元素都大于等于target（或者反过来）。正是因为有了这种“二段性”，我们才能每次拿中间元素和target比，然后果断排除左边或右边的一半，不用逐个遍历。

2.模板：理解逻辑比死记代码重要

二分查找确实有成熟的“模板”，但千万别死记硬背——就像手里握着卡塞尔装备部递来的屠龙武器，却忘了如何激活、如何瞄准，那这把武器反而不如一把普通匕首实用（龙族乱入嘿嘿）。

常见的二分查找模板主要分为以下三种，适用场景各有不同：

模板类型	核心适用场景	特点
朴素二分查找	查找“唯一存在的目标元素”	逻辑最简单，上手快，但局限性强，仅适用于元素无重复的场景（本文题目使用的就是该模板）
查找左边界	查找“目标元素第一次出现的位置”	适用性更广，能处理元素重复的情况，细节点更多（如边界收缩逻辑）
查找右边界	查找“目标元素最后一次出现的位置”	与左边界模板逻辑互补，同样适用于重复元素场景，是解决复杂查找问题的常用工具

其中，后两种模板（左边界、右边界查找）功能性更万能，但涉及的边界处理、循环终止条件等细节也更复杂。咱们明天拆解LeetCode 34题（在排序数组中查找元素的第一个和最后一个位置）时，再逐行梳理这两种模板的逻辑；今天的重点，是通过LeetCode 704题先把最基础的“朴素二分查找”彻底吃透，打好根基。

题目描述：LeetCode 704. 二分查找

题目链接：二分查找

题目描述：

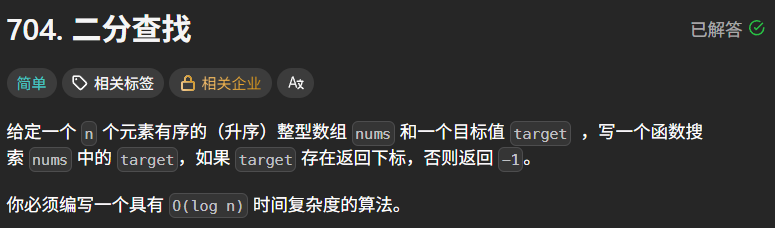
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：
1.你可以假设 nums 中的所有元素是不重复的。
2.n 将在 [1, 10000]之间。
3.nums 的每个元素都将在 [-9999, 9999]之间。

为什么可以用二分查找？

在讨论二分查找时，我们不仅要知道“能用”，更要想清楚“为什么用”，以及“遇到随机题目时怎么和二分关联”——这才是掌握算法的关键 ✨

我们先看“为什么可以用”：二分查找的核心是利用“二段性”缩小范围，而这道题恰好完美契合这个前提→题目中的数组是升序排列的。

假设我们随便选数组中间的元素 nums[mid]，和目标值 target 对比，会立刻出现三种清晰的情况，每一种都能帮我们“砍掉”一半无用的查找范围 🪓：

1. 若 nums[mid] == target 🎯：直接命中答案！不需要再找了，直接返回 mid 即可；
2. 若 nums[mid] > target 📈：因为数组是升序的，mid 右边所有元素都会比 nums[mid] 更大，自然也比 target 大——这半边完全不用看了，下次只查 mid 左边；
3. 若 nums[mid] < target 📉：同理，mid 左边所有元素都会比 nums[mid] 更小，自然也比 target 小——这半边可以直接舍弃，下次只查 mid 右边。

之前提到的“二段性”，在这里也直接体现出来我们通过 mid 和 target 的大小关系，我们能把数组精准分成两部分——一部分是有用的查找范围，另一部分是可以直接扔掉的无效范围。

正因为每次都能把查找范围缩小到原来的 1/2，二分查找才能实现 O(log n) 的高效时间复杂度，这也是它比暴力遍历（O(n)）强的根本原因 💪

暴力算法解法

既然题目要求O(log n)，那肯定不能用暴力，但咱们还是先说说暴力解法，对比一下就能更直观感受到二分的优势。

暴力解法很简单：从头到尾遍历数组，逐个比较元素和target。如果找到相等的，就返回下标；遍历完都没找到，就返回-1。代码大概长这样：

int search(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); i++) {if (nums[i] == target) {return i;}}return -1;
}

这代码肯定能跑通，但时间复杂度是O(n)——如果数组有10000个元素，最坏情况要循环10000次。现在对两个方法的时间复杂度没有太多概念没有关系，后面我们会详细说到

二分查找解法

核心逻辑：三种情况的处理

刚才其实已经说了核心思路：每次取中间元素mid，和target比，然后根据结果缩小范围。具体来说：

1. 初始化左右边界：left = 0，right = nums.size() - 1（因为数组下标从0开始，最后一个元素下标是size-1）
2. 循环查找：只要left <= right就证明再合法范围内（注意这里是“<=”，后面说原因），在这个区间才能继续计算中间下标mid
3. 比较nums[mid]和target：
   • nums[mid] = target：找到目标，记录下标，跳出循环；
   • nums[mid] > target：说明目标在左边，把右边界移到mid - 1（因为mid已经查过了，不用再考虑）
   • nums[mid] < target：说明目标在右边，把左边界移到mid + 1（同理，mid不用再考虑）
4. 如果循环结束都没找到，返回-1。

二分查找什么时候结束？

可能有人会想：为什么循环条件不能用left < right？
比如数组只剩一个元素时，left和right相等，这时候left < right不成立，循环就结束了，那这个元素不就漏查了吗？

比如数组[5]，target是5：初始left=0，right=0，left <= right成立，进去计算mid=0，发现nums[mid]==target，返回0——正确。

如果target是3，数组还是[5]：第一次循环mid=0，nums[mid] > target，所以right=mid-1=-1。这时候left=0，right=-1，left > right，循环结束，返回-1——也正确。

为什么二分查找一定是对的？

这道题中，我们可以明确数组是严格升序排列的，单调性极其明确——正是这个特性，为二分查找“安全缩小范围”提供了根本保障。

只要数组满足单调性（升序或降序），通过“中间元素 nums[mid] 与 target 的大小对比”，就能精准划分“有效范围”与“无效范围”，绝不会出现“漏查目标”的情况：

• 若数组升序：nums[mid] > target → 右半区所有元素均 > target（无效，可舍弃）；nums[mid] < target → 左半区所有元素均 < target（无效，可舍弃）；
• 若数组降序：逻辑相反，但同样能通过一次对比砍掉一半范围。

这种“每次缩小范围都绝对安全”的特性，让二分查找最终要么精准定位到目标（若存在），要么确定目标不存在——不会出现“范围缩错导致漏查”的问题。

数学证明：单调性下二分查找的有效性（数学归纳法）

证明目标：对于非空有序数组 nums（此处以升序为例），若 target 在 nums 中，则二分查找必能找到；若不在，则必能判断不存在。

1. 基础情况（n=1，数组仅1个元素）

• 若 nums[0] == target：直接返回下标0，找到目标；
• 若 nums[0] != target：循环结束，判断目标不存在。
  基础情况成立。

2. 归纳假设（假设数组长度为k时，结论成立）
即：对于长度为k的升序数组 nums，二分查找能正确判断 target 是否存在（存在则返回下标，不存在则返回不存在）。

3. 归纳递推（证明数组长度为k+1时，结论仍成立）
对于长度为k+1的升序数组 nums，取中间下标 mid = left + (right - left) // 2（避免溢出），对比 nums[mid] 与 target：

• 情况1：nums[mid] == target：直接返回mid，找到目标，结论成立；
• 情况2：nums[mid] > target：因数组升序，mid 右侧（共 (k+1)-mid-1 ≤ k 个元素）均 > target，可舍弃，剩余查找范围为 [left, mid-1]（长度 ≤k）。根据归纳假设，对长度≤k的数组，二分查找能正确判断，故结论成立；
• 情况3：nums[mid] < target：因数组升序，mid 左侧（共 mid - left ≤ k 个元素）均 < target，可舍弃，剩余查找范围为 [mid+1, right]（长度 ≤k）。同理，根据归纳假设，结论成立。

综上，当数组长度为k+1时，结论仍成立。

由数学归纳法可知，对任意长度的有序数组，二分查找的有效性均成立——这也是“单调性”为二分查找提供的数学层面的保障。

时间复杂度

二分查找的核心优势在于每次将查找范围缩小为原来的 1/2，这个“减半”过程直到范围为空或找到目标才停止。我们可以通过“查找次数”与“初始范围大小”的对应关系，直观看到时间复杂度为何是 O(log n)。

假设初始查找范围包含 n 个元素，每次缩小后范围大小如下表所示（“第k次查找后”指完成第k轮对比与范围调整后的剩余元素数）：

查找轮次	剩余查找范围大小	对应关系（以2的幂次表示）
初始状态	n	n = 2^log₂n
第1次后	n/2	n/2 = 2^(log₂n - 1)
第2次后	n/4	n/4 = 2^(log₂n - 2)
第3次后	n/8	n/8 = 2^(log₂n - 3)
…	…	…
第k次后	n/(2^k)	n/(2^k) = 2^(log₂n - k)
终止时	≤1	n/(2^k) ≤ 1 → 2^k ≥ n

当查找终止时，剩余范围大小 ≤1（要么找到目标，要么确认目标不存在），此时满足：
n/(2^k) ≤ 1
对不等式变形可得：
2^k ≥ n
两边取以2为底的对数（log₂），根据对数单调性，不等号方向不变：
k ≥ log₂n
由于查找次数 k 必须是整数，因此最多需要 ⌈log₂n⌉ 次查找（⌈x⌉ 表示向上取整，如 log₂100万≈19.93，向上取整为20次）。

举个直观例子： 👇

• 当 n=100万时，log₂100万≈19.93 → 最多只需20次查找；
• 当 n=10亿时，log₂10亿≈29.89 → 最多只需30次查找。
  这就是“对数级复杂度”在数据量大时的压倒性优势。

代码

下面是我写的代码，结合注释咱们再捋一遍细节：

class Solution {
public:int search(vector<int>& nums, int target) {// 初始化左边界为0，右边界为数组最后一个元素的下标int right = nums.size() - 1, left = 0;// 用于记录结果，默认-1（没找到）int ret = -1;// 循环条件：left <= right（确保所有可能的位置都查过）while (left <= right) {  // 🌟 闭区间循环条件！别漏了"="// 计算中间下标：用left + (right - left)/2代替(left+right)/2，避免溢出int middle = left + (right - left) / 2;  // 🌟 防溢出！别写成(right+left)/2// 如果中间元素等于target，找到目标，记录下标并跳出循环if (nums[middle] == target) {ret = middle;break;}// 如果中间元素大于target，说明目标在左边，右边界左移到middle-1else if (nums[middle] > target) {right = middle - 1;}// 如果中间元素小于target，说明目标在右边，左边界右移到middle+1else {left = middle + 1;}}return ret;}
};

这里有个细节必须提：计算middle的时候，为什么用left + (right - left)/2而不是(left + right)/2？

📌 记住：计算mid永远用 left + (right - left)/2，不用(right+left)/2！两者数学结果相同，但前者能避免left和right过大时的整数溢出（比如 left=2^30 ，right=2^30时，right+left会超INT_MAX）。

为什么是二分不是三分、四分？

有人可能会想：既然二分能缩小一半范围，那三分、四分是不是更快？理论上每次缩小更多范围，次数应该更少？

其实不一定。咱们先写个三分查找的例子感受下：

// 三分查找示例（针对升序数组找target）
int ternarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {// 把范围分成三份，找两个中间点int mid1 = left + (right - left) / 3;int mid2 = right - (right - left) / 3;if (nums[mid1] == target) return mid1;if (nums[mid2] == target) return mid2;// 根据target位置缩小范围if (target < nums[mid1]) {right = mid1 - 1;} else if (target > nums[mid2]) {left = mid2 + 1;} else {left = mid1 + 1;right = mid2 - 1;}}return -1;
}

四分查找原理类似，就是分的段更多，中间点更多。

但为什么实际中几乎没人用三分、四分？因为：

• 时间复杂度差距不大：二分是O(log₂n)，三分是O(log₃n)，四分是O(log₄n)。但log₂n ≈ 1.58log₃n ≈ 2log₄n，差距很小。比如n=1e6，二分要20次，三分只要12次，四分只要10次——次数少了，但每次循环里的操作变多了（三分要算两个中间点，判断两次）；
• 代码复杂度上升：分的段越多，边界条件越复杂，越容易出错，维护成本高，而且一点选错成本会更高；
• 实际效率未必更高：虽然次数少，但每次循环的计算、判断步骤多，整体耗时可能反而比二分更长。

咱们可以写个简单的程序测试下（用随机数组+多次查找计时）：

#include <iostream>
#include <vector>
#include <random>
#include <chrono>using namespace std;// 二分查找
int binarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}return -1;
}// 三分查找
int ternarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid1 = left + (right - left) / 3;int mid2 = right - (right - left) / 3;if (nums[mid1] == target) return mid1;if (nums[mid2] == target) return mid2;if (target < nums[mid1]) right = mid1 - 1;else if (target > nums[mid2]) left = mid2 + 1;else {left = mid1 + 1;right = mid2 - 1;}}return -1;
}int main() {// 生成一个100万个元素的升序数组int n = 1000000;vector<int> nums(n);for (int i = 0; i < n; i++) {nums[i] = i;}// 随机生成1000个目标值（确保在数组范围内）random_device rd;mt19937 gen(rd());uniform_int_distribution<> dist(0, n-1);vector<int> targets(1000);for (int i = 0; i < 1000; i++) {targets[i] = dist(gen);}// 测试二分查找时间auto start = chrono::high_resolution_clock::now();for (int t : targets) {binarySearch(nums, t);}auto end = chrono::high_resolution_clock::now();chrono::duration<double> binaryTime = end - start;cout << "二分查找总时间：" << binaryTime.count() << "秒" << endl;// 测试三分查找时间start = chrono::high_resolution_clock::now();for (int t : targets) {ternarySearch(nums, t);}end = chrono::high_resolution_clock::now();chrono::duration<double> ternaryTime = end - start;cout << "三分查找总时间：" << ternaryTime.count() << "秒" << endl;return 0;
}

我跑了几次，二分查找总时间大概在0.0002秒左右，三分查找大概在0.0004秒左右——反而更慢。所以除非是极特殊的场景，否则二分查找是性价比最高的选择，大家可以亲自去试一试。

细节：这些坑别踩

常见问题	正确做法	错误案例（为什么错）
右边界初始化	right = nums.size() - 1	right = nums.size()（可能导致下标越界）
mid计算	left + (right - left)/2	(left+right)/2（left/right过大时溢出）
循环条件	left <= right	left < right（会漏掉left==right时的元素）

三个点联动起来记：“闭区间初始化（右边界取尾下标）+ 安全算 mid + 循环到相等”，二分查找的边界问题基本就绕不开了

快速测试：你能找出这些错误吗？

int search(vector<int>& nums, int target) {int left = 0, right = nums.size();  while (left < right) {  int mid = (left + right) / 2;  if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}return -1;
}

答案：

1. right应初始化为nums.size()-1
2. 循环条件应是left <= right
3. mid计算应是left + (right - left)/2 （也不算错误就是这种写法更优）

总结+预告

今天我们从“二段性”这个核心点出发，拆解了二分查找的基础逻辑，通过LeetCode 704题实现了朴素二分查找的代码，也踩了右边界初始化、mid计算溢出这些常见的“坑”。其实二分查找的本质就是“用条件划分范围，逐步缩小查找空间”，只要抓住这个核心，再复杂的变形也能捋清楚。

不过今天的题目里，数组元素是“不重复”的，所以找到target后直接返回即可。但如果数组里有重复元素，比如[1,2,2,3]，要找2第一次出现的位置或者最后一次出现的位置，朴素二分就不够用了——这就需要用到我们之前提到的“左边界查找”和“右边界查找”模板。

明天要一起研究的是 LeetCode 34题：在排序数组中查找元素的第一个和最后一个位置，有个小问题可以先想想：如果数组是[1,2,2,2,3]，target=2，你觉得“左边界”和“右边界”分别是多少？用今天的朴素二分查找，能直接找到吗？为什么？明天我们就用这个例子拆解“左边界查找”的逻辑～

“喏，Doro给你一朵小花🌸奖励看到这里的你，这篇二分查找的拆解有没有把你心里的‘小疑惑’全捋顺呀？要是你觉得这篇博客把单调性、二段性这些‘小细节’讲得明明白白，就给个点赞鼓励一下嘛~ 要是怕以后找不到这么贴心的讲解，可得赶紧收藏起来！不然下次遇到二分问题，Doro怕你会像Doro一样因为找不到 Orange 时那样‘委屈巴巴’哦~ Doro 知道这个博主后面还会扒更多算法‘小秘密’，关注他，带你从‘看着会’到‘写得对’，再也不被二分的细节‘背刺’啦~，最后的最后Doro把这道题的模板写在这里了，一定要学会再用哦！👇”

朴素二分模板

while(left <= right)
{int mid = left + (right - left)/2;if(.....)//条件left = mid + 1;else if(.....)//条件right = mid -1;elsereturn .....;//找到并返回结果
}