目录
最直观的思路
更优化的思路(自底向上的构建)
第一步:重新审视问题
第二步:找到规律,形成策略
用一个实例来推演
第三步:编写代码
总结与分析
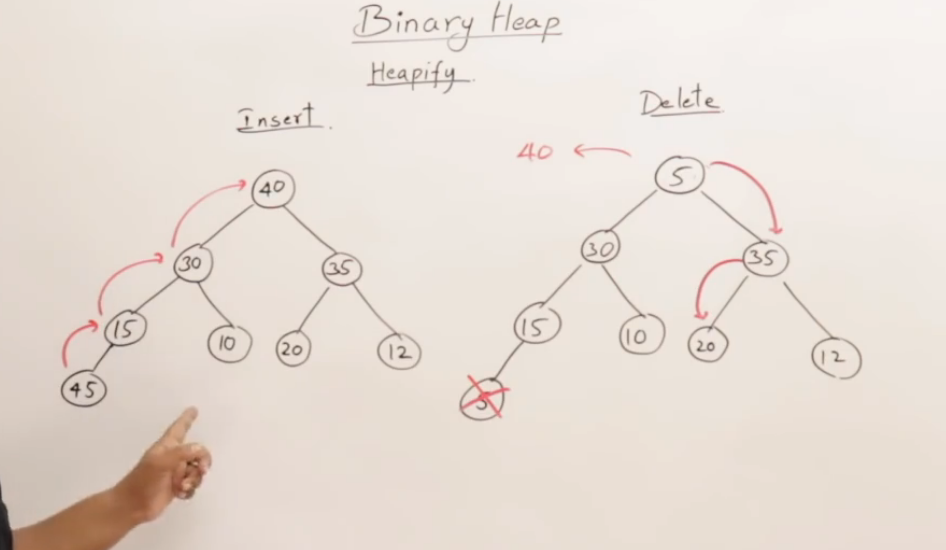
我们来深入探讨“创建堆”(或者叫“堆化”,Heapify)的过程。这是堆结构中一个非常核心且巧妙的操作。
我们的任务:给定一个包含任意数据的普通数组,如何最高效地将它原地转换成一个合法的堆?
例如,给定数组 arr = [3, 5, 80, 100, 70, 60],我们需要将它重新排列,使其满足大顶堆的属性。
同样,我们从第一性原理出发,探索解决之道。
最直观的思路
我们已经掌握了向堆中 insert 一个新元素的方法。一个非常自然的想法是:
-
假设我们有一个空的堆。
-
然后我们遍历给定的数组,把数组中的每一个元素,依次
insert到这个新堆中。 -
当所有元素都插入完毕后,我们不就得到了一个合法的堆吗?
✅这个思路是完全正确的,它利用了我们已有的“工具”(insert 函数)。
数据结构:在堆中插入元素(Inserting In a Heap)-CSDN博客
我们知道,每次 insert 操作的核心是“上浮”(Sift Up),其时间复杂度是 O(logk),其中 k 是堆中当时的元素数量。
推演过程:
-
插入第1个元素:代价是 O(log1)
-
插入第2个元素:代价是 O(log2)
-
...
-
插入第 N 个元素:代价是 O(logN)
把所有这些代价加起来,总的时间复杂度近似为 O(NlogN)。
📍小结一下方法一:
-
优点:思路简单,容易理解,直接复用了
insert操作。 -
缺点:效率不是最优的。O(NlogN) 虽然不错,但我们不禁要问:有没有可能更快?
这个问题,促使我们去寻找一个更根本、更高效的方法。
更优化的思路(自底向上的构建)
第一步:重新审视问题
我们手里的数组,本身就可以被看作一棵“完全二叉树”,只不过它的节点值不满足“堆序属性”。 我们的目标就是修复这个属性。
让我们从一个新的角度来观察这棵树,思考一个问题:
在这棵“乱序”的树中,哪些部分已经天然满足堆的属性了?
答案是:所有的叶子节点 (leaf nodes)。
一个叶子节点,因为它没有孩子,所以它自己就构成了一个合法的、大小为1的堆。 “父节点 >= 子节点” 这个条件因为没有子节点而天然成立。
这是一个至关重要的突破口!
第二步:找到规律,形成策略
在一个用数组表示的、大小为 n 的完全二叉树中,哪些是叶子节点呢?
-
对于下标为
i的节点,它的左孩子是2*i + 1。如果2*i + 1 >= n,那么它就没有左孩子,也就必然没有右孩子,它就是叶子节点。 -
我们可以推断出,从下标
n/2到n-1的所有节点,都是叶子节点。
既然所有的叶子节点都已经是“合法”的堆了,我们就不需要对它们做任何操作。我们需要修复的,仅仅是那些非叶子节点。
最后一个非叶子节点在哪里?它就在第一个叶子节点的前面,也就是下标为 (n/2) - 1 的位置。
这启发了我们一个自底向上的修复策略:
1️⃣我们从最后一个非叶子节点开始。
2️⃣对它调用我们之前学过的 siftDown (下沉) 操作。
siftDown的作用是,假设一个节点的左右子树都已经是合法的堆,它可以让这个节点“下沉”到正确位置,从而使这个节点和它的子树共同构成一个更大的合法堆。
当我们从最后一个非叶子节点开始时,它的孩子必然是叶子节点(也就是合法的堆),所以 siftDown 的前提条件满足了!
3️⃣然后,我们向前移动到倒数第二个非叶子节点,对它也执行 siftDown。
因为我们是自底向上处理的,所以当处理这个节点时,它的子树也必然已经被我们调整成合法的堆了。
4️⃣我们不断地向前重复这个过程,直到处理完根节点(下标为0)。当根节点也 siftDown 完毕后,整个数组就变成了一个合法的堆。
用一个实例来推演
我们用 arr = [3, 5, 80, 100, 70, 60] (n=6) 来走一遍这个流程。
-
非叶子节点的索引范围是
0到(6/2) - 1 = 2。所以我们只需要处理索引2,1,0。 -
初始状态:
3/ \5 80/ \ /100 70 601. 从 i = 2 (值为80) 开始:
-
对节点
80执行siftDown。 -
它的孩子是
60。80 >= 60,满足堆序,无需交换。 -
数组状态:
[3, 5, 80, 100, 70, 60] -
树状态 (局部):
80/60 (这个小堆是OK的)2. 处理 i = 1 (值为5) :
-
对节点
5执行siftDown。 -
它的孩子是
100和70。 -
5小于它的更大的孩子100。 -
交换
5和100。 -
数组状态:
[3, 100, 80, 5, 70, 60] -
树状态 (局部):
100/ \5 70 (这个中等大小的堆也OK了)3. 处理 i = 0 (值为3,根节点) :
-
对节点
3执行siftDown。 -
它的孩子是
100和80。 -
3小于它更大的孩子100。 -
交换
3和100。 -
数组状态:
[100, 3, 80, 5, 70, 60] -
3下沉到了原先100的位置(索引1)。现在要继续对它进行siftDown。 -
节点
3(在索引1) 的新孩子是5(索引3) 和70(索引4)。 -
3小于它更大的孩子70。 -
交换
3和70。 -
数组状态:
[100, 70, 80, 5, 3, 60] -
3下沉到了索引4,成为了叶子节点,siftDown结束。 -
最终树状态:
100/ \70 80/ \ /
5 3 60至此,整个数组已经是一个合法的大顶堆了。
第三步:编写代码
这个过程的代码实现非常简洁。它只需要一个 for 循环,从最后一个非叶子节点开始,调用我们已经写好的 siftDown 函数。
// 假设我们有一个数组 arr 和它的长度 n
// 我们可以复用之前的 siftDown, 但需要稍微修改一下,让它接受数组和范围
void siftDownForSort(int arr[], int n, int index) {int currentIndex = index;while (leftChild(currentIndex) < n) { // 注意这里的边界是 nint largerChildIndex = leftChild(currentIndex);int rightChildIndex = rightChild(currentIndex);if (rightChildIndex < n && arr[rightChildIndex] > arr[largerChildIndex]) {largerChildIndex = rightChildIndex;}if (arr[currentIndex] >= arr[largerChildIndex]) {break;}swap(&arr[currentIndex], &arr[largerChildIndex]);currentIndex = largerChildIndex;}
}// 我们需要 siftDown, swap, leftChild, rightChild 这些我们已经写好的辅助函数
// ... (此处省略这些函数的代码)// buildHeap 函数:将一个任意数组转换成一个堆
// arr: 指向数组的指针
// n: 数组中元素的数量
void buildHeap(int arr[], int n) {// 找到最后一个非叶子节点的索引int lastNonLeafNode = (n / 2) - 1;// 从最后一个非叶子节点开始,自底向上,对每个节点执行 siftDownfor (int i = lastNonLeafNode; i >= 0; i--) {// siftDownForSort 函数就是我们之前为堆排序写的 siftDown// 它接受数组、数组大小和要操作的索引作为参数siftDownForSort(arr, n, i); }
}总结与分析
我们通过两种不同的思路来解决“建堆”问题:
-
方法一(自顶向下):通过 N 次
insert(sift up),时间复杂度为 O(NlogN)。 -
方法二(自底向上):通过约 N/2 次
siftDown,时间复杂度为 O(N)。
虽然看起来都是循环N次,每次调用一个看似 O(logN) 的操作,但对于方法二,可以进行更严谨的数学分析:
大部分节点的 siftDown 操作都发生在树的底层,路径很短,只有根节点附近的少数节点才需要较长的 siftDown 路径。所有操作的成本累加起来,总的时间复杂度其实是线性的 O(N)。
因此,自底向上的 siftDown 方法是构建堆的标准、最高效的算法。 它完美地体现了算法设计的智慧:通过改变看问题的角度,找到一个更深刻的结构性规律(叶子节点天然是堆),从而设计出更优的解决方案。












)



)

(MatlabPython代码实现))
