1、移动零（同向分3区域）

283. 移动零 - 力扣（LeetCode）

题目：

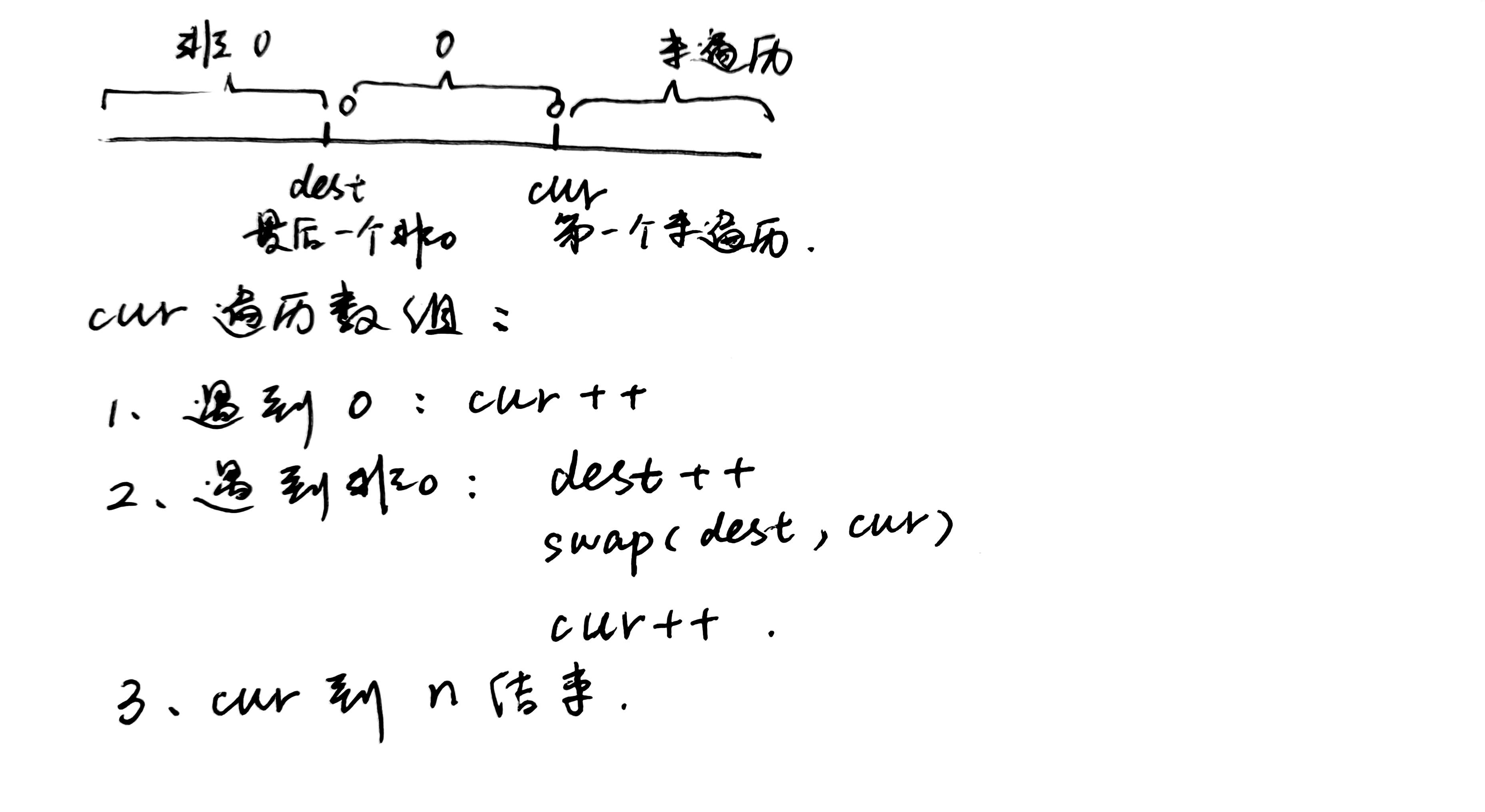
思路：注意原地操作。快排也是这个方法：左边小于等于 tmp，右边大于 tmp，最后 tmp 放到 dest。

代码：

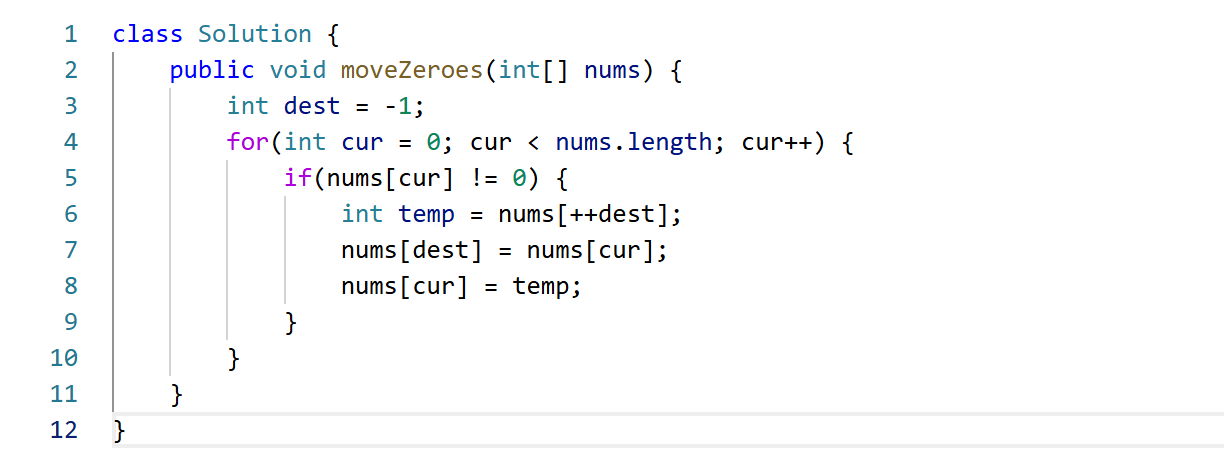
时间复杂度：0(n)

空间复杂度：0(1)

2、复写零（同向模拟操作）

题目：1089. 复写零 - 力扣（LeetCode）

思路：注意就地操作。

代码：

class Solution {public void duplicateZeros(int[] arr) {// 求最后一个抄写数int cur = -1;int dest = -1;int len = arr.length;while(dest < len - 1) {cur++;if(arr[cur] != 0) {dest++;} else {dest += 2;}}// 从后往前抄写// 特殊处理if(dest == len) {arr[len-1] = 0;dest -= 2;cur--;}for(; cur >= 0; cur--) {arr[dest] = arr[cur];dest--;if(arr[cur] == 0) {arr[dest] = arr[cur];dest--;}}}
}

时间：n+常数=n

空间：3=1

3、快乐数（龟兔测循环链路）

题目：202. 快乐数 - 力扣（LeetCode）

思路：

代码：

class Solution {// f 函数private int fun(int n) {int sum = 0;while(n > 0) {int tmp = n % 10;sum += tmp*tmp;n /= 10;}return sum;}public boolean isHappy(int n) {int slow = fun(n);int fast = fun(fun(n));while(slow != fast) {slow = fun(slow);fast = fun(fun(fast));}if (slow == 1) {return true;} else {return false;}}
}

时间：n

空间：2=1

4、盛水最多的容器（单调性，相撞）

题目：11. 盛最多水的容器 - 力扣（LeetCode）

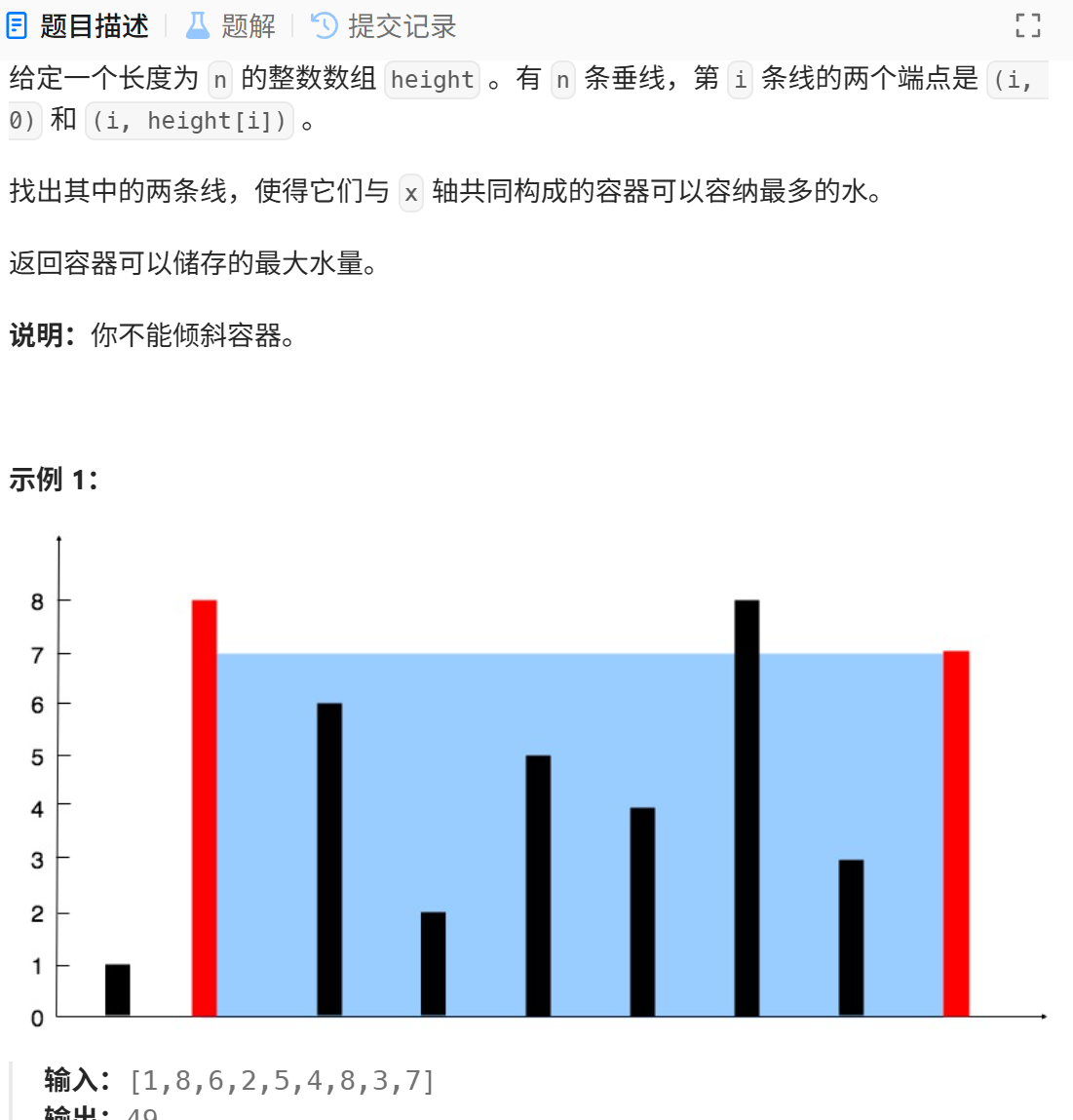
思路：

代码：

class Solution {public int maxArea(int[] height) {int left = 0;int right = height.length - 1;int max_r = 0;while(left < right) {int min_len = Math.min(height[left], height[right]);int tmp = (right - left) * min_len;if(min_len == height[left]) left++;else right--;if(tmp > max_r) {max_r = tmp;}}return max_r;}
}

时间：n

空间：1

5、有效三角形个数（单调性，相撞）

题目：611. 有效三角形的个数 - 力扣（LeetCode）

思路：图中更优指，对于暴力枚举，三角形判断，法二更优。

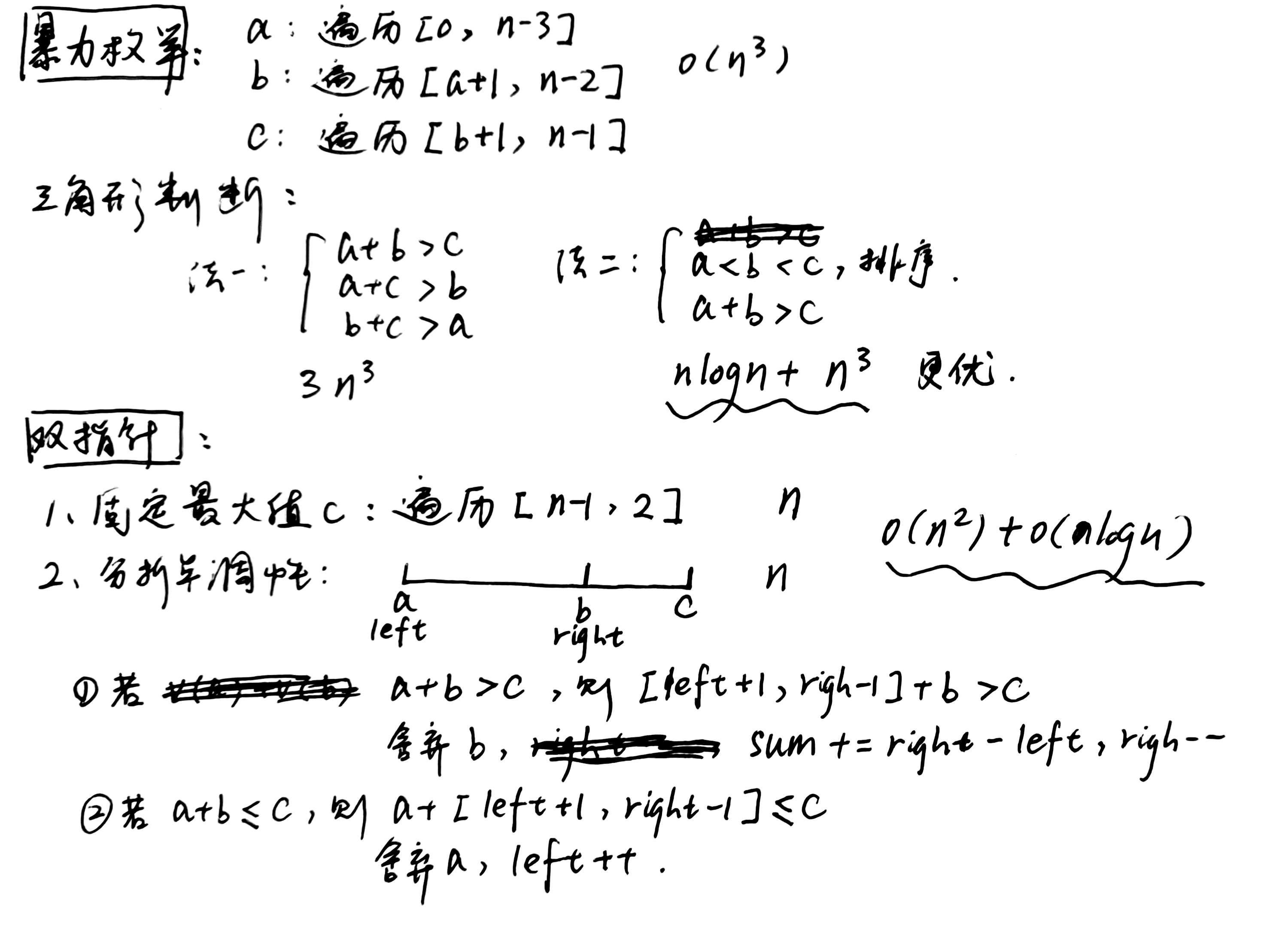
代码：

class Solution {public int triangleNumber(int[] nums) {Arrays.sort(nums);int sum = 0;for(int i = nums.length-1; i >= 2; i--) {// 固定最大值int c = nums[i];// 单调性规律int left = 0;int right = i-1;while(left < right) {if(nums[left] + nums[right] > c) {sum += right - left;right--;}else left++;}}return sum;}
}

6、和为 s 的两个数字（单调性，相撞）

题目：LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

思路：注意升序

代码：

class Solution {public int[] twoSum(int[] price, int target) {int left = 0;int right = price.length-1;while(left < right) {if(price[left] + price[right] > target) right--;else if(price[left] + price[right] < target) left++;else return new int[]{price[left], price[right]};}// 没找到return new int[]{};}
}