二叉树深搜：在算法森林中寻找路径

专栏：算法的魔法世界

个人主页：手握风云

一、搜索算法

二、回溯算法

三、例题讲解

3.1. 计算布尔二叉树的值

3.2. 求根节点到叶节点数字之和

3.3. 二叉树剪枝

3.4. 验证二叉搜索树

3.5. 二叉搜索树中第 K 小的元素

3.6. 二叉树的所有路径

一、搜索算法

BFS和DFS

广度优先搜索（BFS）和深度优先搜索（DFS）是两种常用的图和树的遍历算法，遍历是形式，目的是搜索，在某种形式上，遍历算法与搜索算法可以等价。

BFS 的核心思想是从一个节点开始，逐层遍历所有可达的节点，直到找到目标节点或遍历完所有节点。DFS 的核心思想是从一个节点开始，沿着一条路径尽可能深地搜索，直到无法继续前进时，再回溯到上一个节点，继续搜索其他路径。

暴搜

暴力搜索是一种简单的搜索方式，通过暴力枚举所有的情况来找出结果，通常基于BFS和DFS实现。暴力搜索通常应用于用于解决那些没有明显规律或优化方法的问题，尤其是在数据规模较小时，但有时效率会特别低。

二、回溯算法

回溯算法是一种通过递归搜索所有可能的候选解来找出所有解的算法，它没有那么神秘，本质上其实就是DFS。回溯算法通常可用于迷宫求解，如下图所示，从起点进入并走出迷宫，按照深搜的思路，沿着一条路径走。如果是死胡同，就回溯走另一条路径，再次按照DFS，递归搜索和回溯找到迷宫出口。如果在搜索之前，我们知道这个答案不是我们想要的，我们就直接可以舍弃，这个过程就叫剪枝。

三、例题讲解

3.1. 计算布尔二叉树的值

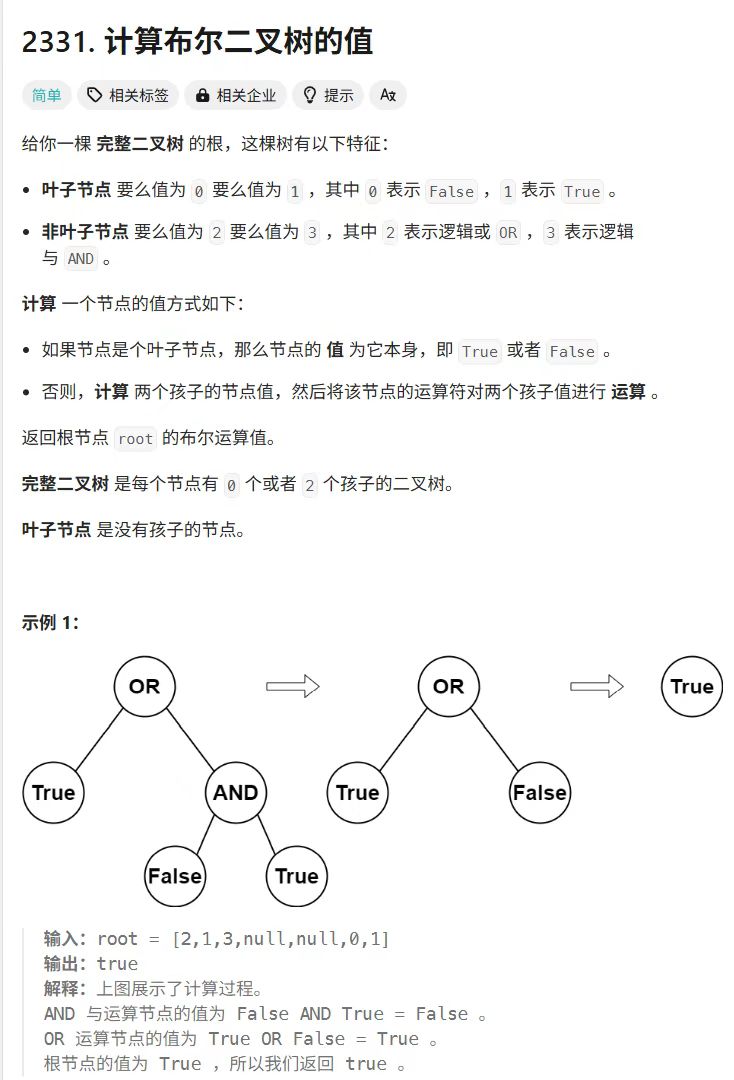
本题中给出的是完整二叉树，要么没有节点，要么左右孩子节点都有。其中叶子节点储存的是真值，非叶子节点储存的是逻辑与、或。我们以示例1为例，0合取1，结果为0；0析取1，结果为1，返回真。

宏观角度：从上面的示例中我们可以得出，这棵树是从下往上推导的。当我们只看根节点时，我们得知道左子树的值，同时也得知道右子树的值，然后在根节点这一层进行整合。而关于求出左右子树的布尔值，与前面的问题是一样的，只需要传入一个引用，即可返回布尔值，这就是递归方法头与方法体的设计。当我们遍历到叶子节点时，不需要判断它的左右子树是否为空，只需要进行逻辑运算即可，这同时也是递归的出口。

细节角度：因为计算过程是从下往上，我们可以看作是二叉树的后序遍历。从根节点出发，先去遍历左子树，当遇到叶子节点时，返回该节点的布尔值，然后回溯到它的父亲节点，然后遍历右子树，再回溯父亲节点并遍历自身。

完整代码实现：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {if (root.left == null) {return root.val == 1;}boolean left = evaluateTree(root.left);boolean right = evaluateTree(root.right);return root.val == 2 ? (left || right) : (left && right);}
}

3.2. 求根节点到叶节点数字之和

需要计算出从根节点出发到所有叶子节点的每一条路径所表示的数字，然后将这些数字相加，得到的总和就是最终要求的结果。即要找出二叉树中所有从根到叶子的路径所对应的数字，并把它们累加起来。

以下图为例，当我们递归到“9”这一层时，我们就需要把“4”先传进来，计算得到49。再把"49"继续向下递归，计算得到495、491，然后返回，直到返回到根结点。那递归的方法头可以设计两个参数，一个根结点和一个路径和presum，返回值为根结点所连接的叶子结点的数字之和。方法体的执行下图中的4步。递归的出口则为遇到叶子结点时，返回路径之和。

完整代码实现：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumNumbers(TreeNode root) {return dfs(root,0);}private int dfs(TreeNode root,int preSum) {preSum = preSum * 10 + root.val;if (root.left == null && root.right == null) {return preSum;}int ret = 0;if (root.left != null) ret += dfs(root.left,preSum);if (root.right != null) ret += dfs(root.right,preSum);return ret;}
}

3.3. 二叉树剪枝

题目要求移除所有不包含1的子树，也就是说，如果一个节点没有任何子节点且其值为0，那么这个节点就应该被删除。

如果我们想剪掉某一棵子树，必须先知道左右子树的信息，所以我们一定是要采用后序遍历来实现。当我们遍历到某一节点时，如果发现左右子树均为空，并且节点值为0，那我们就可以把这个节点剪掉。而我们返回它的父亲节点时，需要加一个返回值将其置为空，然后继续判断。如果节点值为1，那我们就直接返回它的父亲节点就可以了。那我们设计递归方法的时候，只需传入一个根节点，然后去遍历它的左右子树，根据返回值来判断是否该剪掉。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode pruneTree(TreeNode root) {if (root == null) {return null;}root.left = pruneTree(root.left);root.right = pruneTree(root.right);if (root.left == null && root.right == null && root.val == 0) {root = null;}return root;}
}

3.4. 验证二叉搜索树

根据前面学过的知识，对一棵二叉搜索树进行中序遍历，得到的结果是一个有序序列，所以我们可以先定义一个全局变量prev，当遍历到某一个节点时，用prev存储前一个节点值，如下图所示，根据中序遍历，当我们遍历到1时，将prev赋值为1，然后进行比较，后面的数如果越来越大，那就是二叉搜索树。当遍历到19时，会发现19比20小，整棵树就不是二叉搜索树。那么我们就可以通过剪枝，省去处理右子树的过程，直接向上返回一个false。

完整代码实现：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {long prev = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if (root == null) return true;boolean left = isValidBST(root.left);//剪枝if(left == false) return false;boolean cur = false;if (root.val > prev) cur = true;prev = root.val;boolean right = isValidBST(root.right);return left && cur && right;}
}

3.5. 二叉搜索树中第 K 小的元素

仿照上一题的思路，利用两个全局变量，其中一个变量是在中序遍历时充当计数器，另一个变量去标记第K小的结果。进行中序遍历，当遍历到第一个节点时，count--，直到count=0时，说明已经到了第k个节点，此时进行剪枝，把ret更新为17，无需遍历其它子树。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {int count;int ret;public int kthSmallest(TreeNode root, int k) {count = k;InOrder(root);return ret;}public void InOrder(TreeNode root) {if (root == null || count == 0) return;InOrder(root.left);count--;if (count == 0) ret = root.val;if (count == 0) return;InOrder(root.right);}
}

3.6. 二叉树的所有路径

给定一个二叉树的根节点，然后找出所有从根节点到叶子节点的路径。每条路径都应该以字符串的形式返回，路径中的节点值之间用箭头“->”连接。

我们先弄一个字符串变量path，在进行前序遍历的时候，记录每个路径的字符串，当遇到叶子节点时，丢进顺序表List<String> ret中。但如果我们遍历完一条路径后，回溯就会出现问题，比如我们遍历完"1->2->4"，回溯到节点2时，也会返回这个结果，所以我们还需要进行恢复现场的操作，把字符4移除。当我们把节点2处理完返回到节点1时，我们需要移除的是"2->"，所以这个过程就会非常麻烦。我们可以把这个变量放在递归方法的参数里，那我们的方法头就可以设计成DFS(root,path)。当递归方法执行的时候，如果是叶子节点，不需要加上"->"；如果不是叶子节点，需要加上"->"。当某个节点的左子树为空而右子树不为空，那就不需要执行DFS(root.right,path)，直接返回。

完整代码实现：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {List<String> ret;public List<String> binaryTreePaths(TreeNode root) {ret = new ArrayList<>();DFS(root,new StringBuffer());return ret;}public void DFS(TreeNode root,StringBuffer _path) {StringBuffer path = new StringBuffer(_path);path.append(Integer.toString(root.val));if (root.left == null && root.right == null) {ret.add(path.toString());return;}path.append("->");if (root.left != null) DFS(root.left,path);if (root.right != null) DFS(root.right,path);}
}