1 3D到2D透视投影
三维空间上点 p 投影到二维空间 q 有两种方式:1)正交投影,2)透视投影。
正交投影直接舍去 z 轴信息,该模型仅在远心镜头上是合理的,或者对于物体深度远小于其到摄像机距离时的近似模型。
常规镜头成像可以使用透视投影建模,如下图:
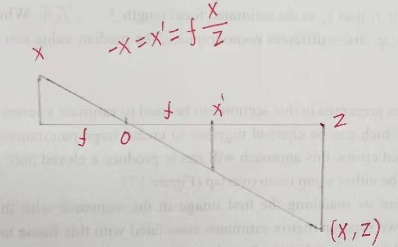
三维空间点 p=(X,Y,Z) 投影到二维空间点 q = (x,y),镜头光轴在 Z 轴上,满足关系

,
真实的物理模型将 X 投影到 x, 但使用

可以避免关系式中产生一个负号,因此投影点可写为

, 同理,有

。
使用矩阵可表示为

,变换结果

为齐次坐标,

。
以上变换举证前三列可表达相机自身相关性质,被称为内参,比如

,其中, f 表示相机焦距,af表示像元横纵比(一般情形下为 1),
cx,cy 表示 CCD 中心与光轴间平移距离,s 表示了 CCD 法向量与光轴不平行程度。
在实际应用中,一般会使用简单模型

,该模型仅表达了焦距与CCD中心平移。
如果将以上变换矩阵改写成满秩矩阵,那么其逆变换就变得很简单,使用 4*4 变换矩阵重新构造透视投影如下:

,
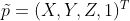
,

,
改写齐次坐标

,前两个分量表示图像上坐标值,第四个分量表示深度信息。
以上透视投影模型要求三维空间坐标满足以下条件:
1)以镜头光心(小孔成像中的小孔)为原点;
2)Z轴垂直与 CCD 平面;
3)XY轴与 CCD 平面 xy 轴平行;
但在实际三维坐标系可能是任意建立的,所以在透视投影前需要变换坐标系,使用平移+旋转模型如下:

,其中,R 为 3*3 旋转矩阵,t 为平移向量。
综上,任意三维空间上点到二维平面的透视投影可表示为

,

,
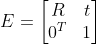
。
2 成对图像配准
如上图(a)所示,三维空间上点 p 映射到图像平面为
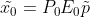
,由于
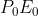
均为满足矩阵,故其逆矩阵一定存在,有

。
结合
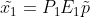
可建立

与

之间的关系为

。
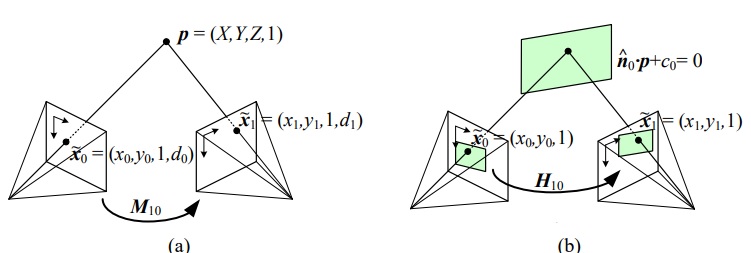
以上关系需要相机记录成像点深度信息,一般相机无法记录深度信息,因此,可以使用图像 (b)建立关系:
假设所有三维空间上点均在一个空间平面上,即满足

,
当进行投影变换时,其深度信息为零, 具体可表达为

,
观察可知,删除变换矩阵最后一行与最后一列不影响计算结果,因此,可简化表达式为

,
以上变换有 8 个自由度,将变换矩阵重新改写为

,
变换矩阵

表达了平面场景的映射关系,这正好是 “图像配准” 一文中使用的模型之一。
3 旋转全景模型
在一个固定的世界坐标下,假设相机绕某旋转点旋转拍照,两次(或多次)拍照间相机坐标原点保持不变,但光轴随旋转发生改变。
三维空间中任意固定点在每次拍照中的映射可表达为:
1)建立相机坐标系(原点与世界坐标系一致,光轴为相机当前光轴);
2)使用旋转矩阵 R 将世界坐标系下点旋转为相机坐标系下点;
3)使用投影矩阵投影到相机平面;
因此,三维空间点在两幅图像中的映射关系可简化为
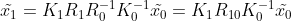
,
假设 K 仅包含相机焦距信息,则

,
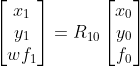
,当焦距已知时,此参数仅为旋转,当焦距未知时,可以是固定焦距或者变化焦距。
一般情况下,该变化的参数个数为 4,包括 1)固定未知焦距,2)旋转参数(3个),
这比8个参数投影变换更加简化,该模型是用于全景图像拼接的理想模型。
4 迭代求解
给定一对图像上若干匹配点

,使用平面投影变换可得

,
两边同时乘以分母得

,
进一步整理为

,
使用该线性方程组可以求解变换矩阵

的初始估计。
在初始估计
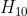
基础上使用非线性迭代方程为

,

,

为变换矩阵
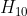
的估计,

为第二次迭代估计,通过最小化第二次估计误差即求得合理的

。
如果在每次迭代估计中使用上次迭代估计值

作为初始估计,即

中各个参数值均为零,迭代方程可改写为
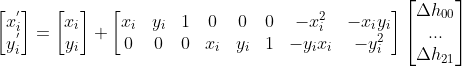
,
注意,以上

不再是初始匹配点,而是每次迭代后的计算点!!!
在旋转全景模型中,
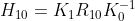
,当旋转分量增加

后,
旋转矩阵为
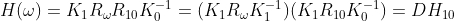
,
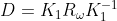
为增量矩阵。

,当

为弧度单位且很小时,
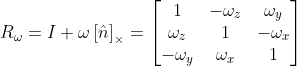
,
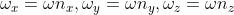
,

表示旋转轴。
增量矩阵 D 可改写为

,
D 中变量为旋转角度

,使用线性近似可表达为
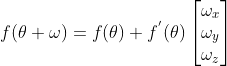
,
其中,

为初始估计参数的变换结果,

为旋转一个小的角度

后的线性变换结果,
使用最小二乘法可以求解一个合理的旋转角度。
观察增量矩阵 D,可以发现 D 与 H 存在一种对应关系
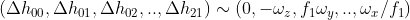
,
迭代公式
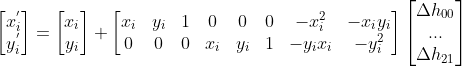
可转换为:
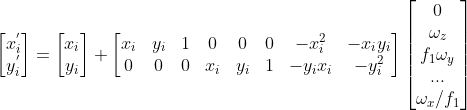
,
整理公式,使其为

的线性函数
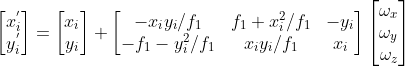
,
使用最小二乘法可以求解一个合理的旋转角度。
以上迭代公式中,

是一个未知量,但是可以从初始估计

中计算得出,具体如下:

,

,

,该旋转矩阵为正交矩阵,
在旋转矩阵每一项上乘以一个因子
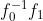
不会改变矩阵正交特性,因此,可将上式改写为:

,利用正交特性有:
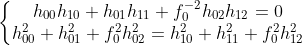
,可求解

,
同理,利用第三行与第一行正交可求解

,当焦距相等时,可估计焦距为
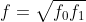
。
5 全局配准
由于每对图像间的配准估计均可能存在误差,当多幅图像通过图像对间配准参数配准时,会形成累积误差,
这在全景图像拼接中可能产生缝隙或者过叠加,所以需要校正图像对间配准参数,称作光束平差法(bundle adjustment)。
在光束平差法之前,通过图像对间特征点匹配情况可以剔除一些孤立图像,然后在保留图像中进行全局配准。
假设有 n 帧图像用于形成全景图像,三维空间中有 m 个特征点在至少两帧图像中形成了映射关系,
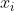
表示第 i 个三维空间点,

表示第 i 个三维空间点在第 j 帧图像上形成的投影点,

表示得 i 个三维空间点在第 j 帧图像上是否存在投影点。
利用旋转全景模型可建立
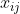
到

的映射为
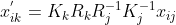
,
最小化

即可。
完成全局配准后,全景图像仍然可能存在局部错位,这可能是因为镜头镜像畸变,摄像头没有完全绕光轴中心旋转,场景中微小抖动等因素引起。
可以通过对整幅全景图像建立一个类似稠密光流估计图来抵消局部误差,方法如下:
1)已经通过光束平差法重新估计了变换矩阵;
2)利用
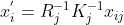
计算第 j 帧图像对应的第 i 个特征点位置;
3)求所有图像帧上对应的第 i 个特征点的平均位置

;
4)求第 i 个特征点在第 j 帧图像上的精确位置
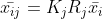
;
5)求第 i 个特征点在第 j 帧图像上扰动

;
6)使用插值构造全景图像上局部扰动,用于全景拼接时补偿局部模糊。
6 图像合成
当所有相关图像都完成注册后,我们可以利用以上信息产生一张完整的拼接图像,这个过程大致包括以下内容:
1)选择合成表面,当少量图像拼接时,可以选择平坦全景图;当全景图视野很大时,如果选择平坦全景图,
则在周边区域会产生很大扭曲变形,这时一般选择圆柱面投影或者球面投影;
2)决定那一帧图像作为中间参考图像,由于已经知道每一帧图像对应的旋转角度,一般旋转平均旋转角度附近的图像作为中间参考图像;
3)将参考图像平移到合成表面中心,将其他图像按已知注册信息映射到合成表面;
4)在重叠部分通过加权方式去除虚影;
5)使用拉普拉斯金字塔融合方案融合图像,必要时进行曝光补偿。

Java/python/JavaScript/C/C++/GO最佳实现)

)















