1.树

1.1.树的概念

树是一种非线性的数据结构，是由n(n>=0)个有限结点组成的具有层次关系的集合

• 树的结构类似于一棵倒挂的树(根在上，枝叶在下)
• 根节点是一个特殊的结点，它没有前驱结点
• 除去根结点，其余结点又被分成了m(m>=0)个集合，这些集合被称为根结点的子树
• 每个子树又是一个与树相似的结构，都只有一个前驱，有0或多个后继，因此树是递归定义的

1.2.树的结构

在树形结构中，子树之间不能有交集，否则就是非树形结构
非树形结构：

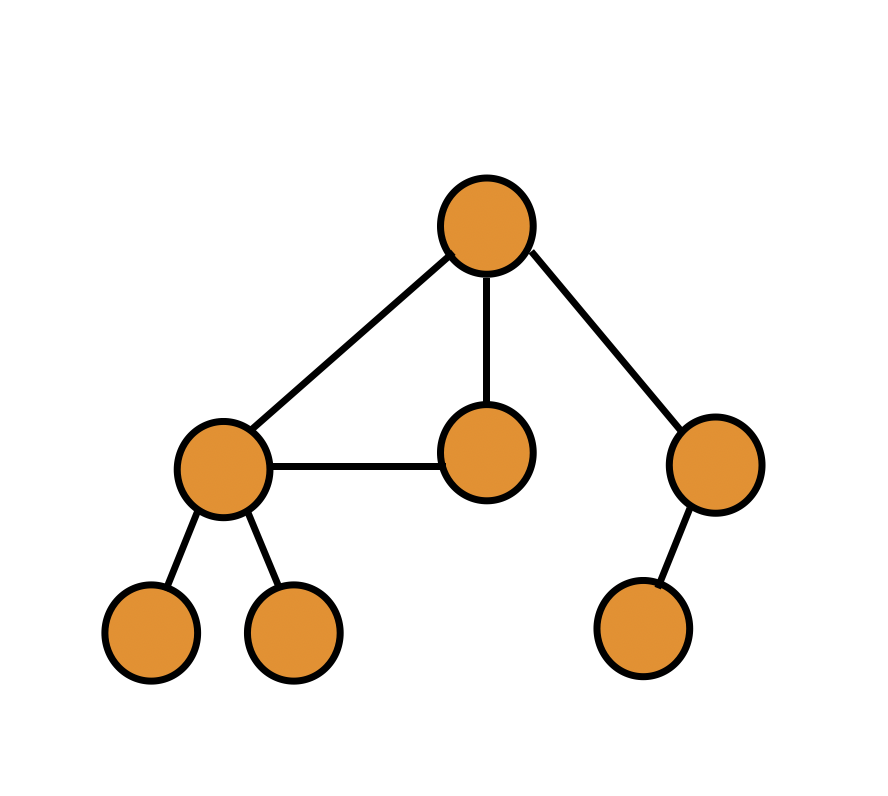
1.3.树的相关术语

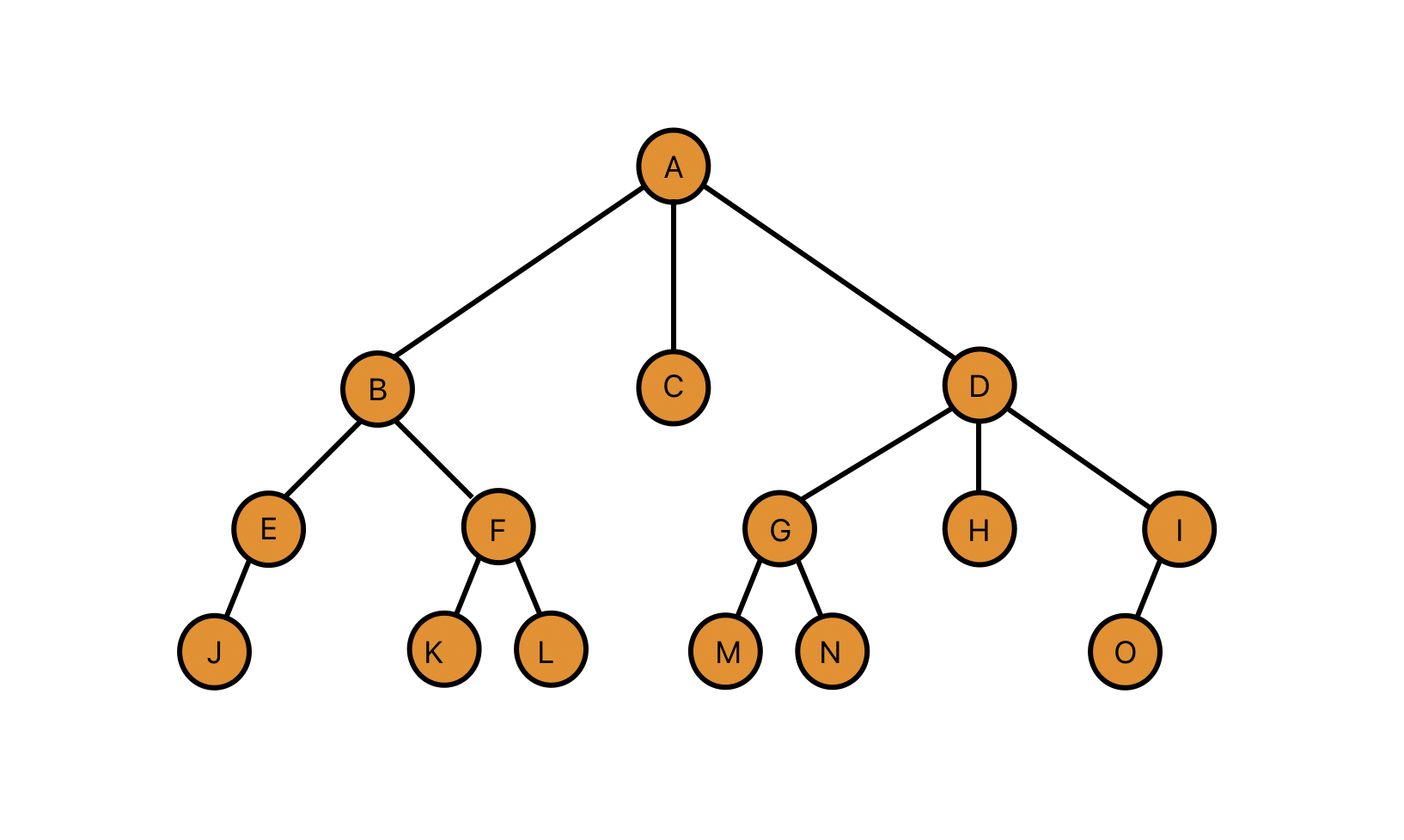
父结点/双亲结点：若一个结点含有前驱结点，则这个前驱结点就是该结点的父结点，如图：A是B、C、D的父结点，B是E、F的父结点···
子结点/孩子结点：若一个结点有后继节点，那么这个后继结点就是该结点的子结点，如图：B是A的子结点，G是D的子结点···
结点的度：一个结点含有的子结点个数就是该结点的度，如图：A的度为3，C的度为0···
树的度：一棵树中，我们把所有结点中最大的度，称为树的度，如图：度为3(A和D的度最大)
叶⼦结点/终端结点：度为0的结点，如图：J、K、L、M···
分⽀结点/⾮终端结点：度不为 0 的结点，如图：B、C、D、E、F···
兄弟结点：具有相同⽗结点的结点互称为兄弟结点(亲兄弟)，如图：B、C 是兄弟结点
结点的层次：从根开始定义起，根为第 1 层，根的⼦结点为第 2 层，以此类推
树的⾼度或深度：树中结点的最⼤层次，如图：高度为4
结点的祖先：从根到该结点所经分⽀上的所有结点，如图： A是所有结点的祖先
路径：⼀条从树中任意节点出发，沿⽗结点-⼦结点连接，达到任意节点的序列，⽐如A到O的路径为：
A-D-I-O
⼦孙：以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙，如图：所有结点都是A的⼦孙
森林：由 m（m>0） 棵互不相交的树的集合称为森林

2.二叉树

2.1.二叉树的概念

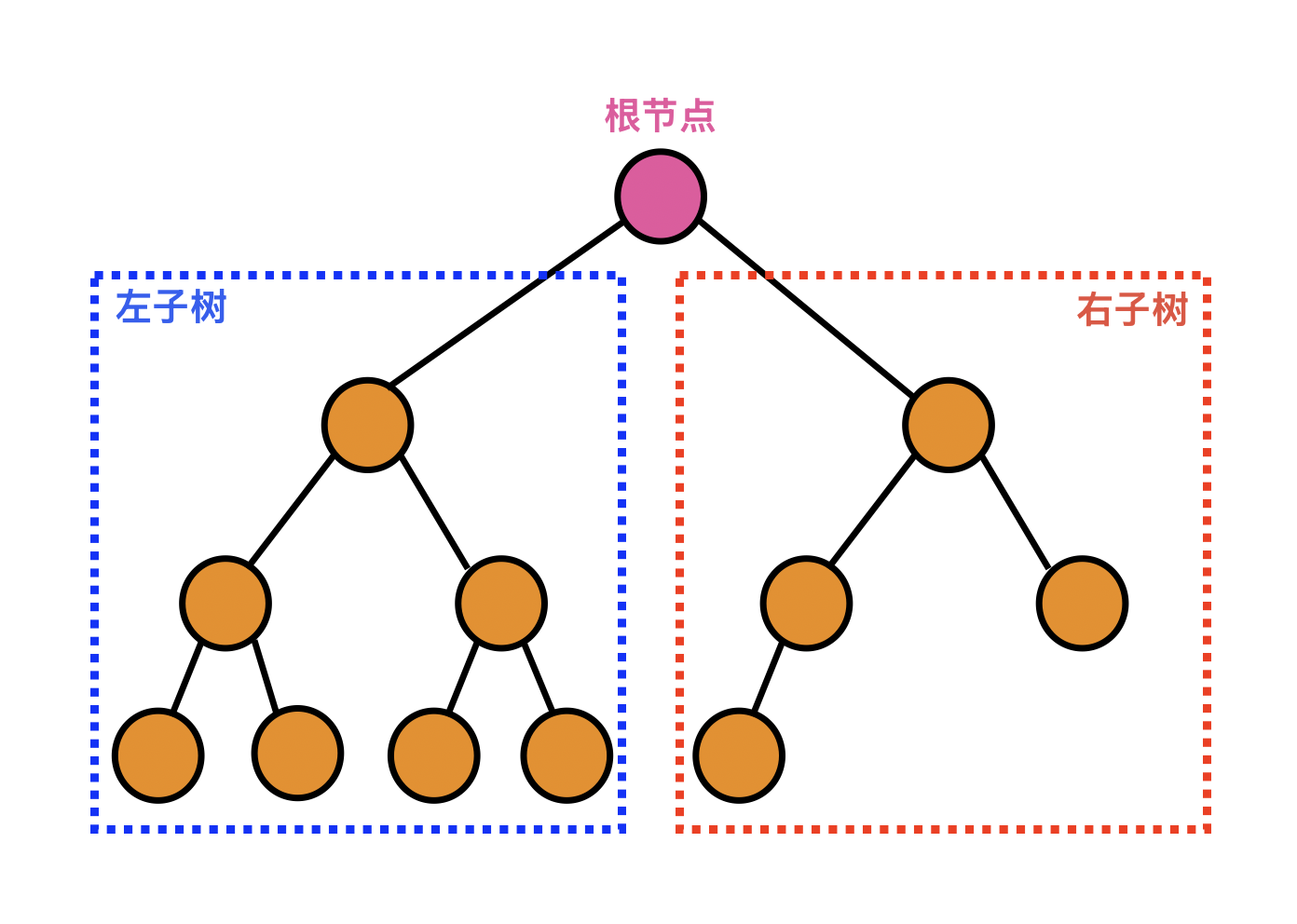
二叉树是最常见的树形结构结构，通常由一个根节和两课子树构成

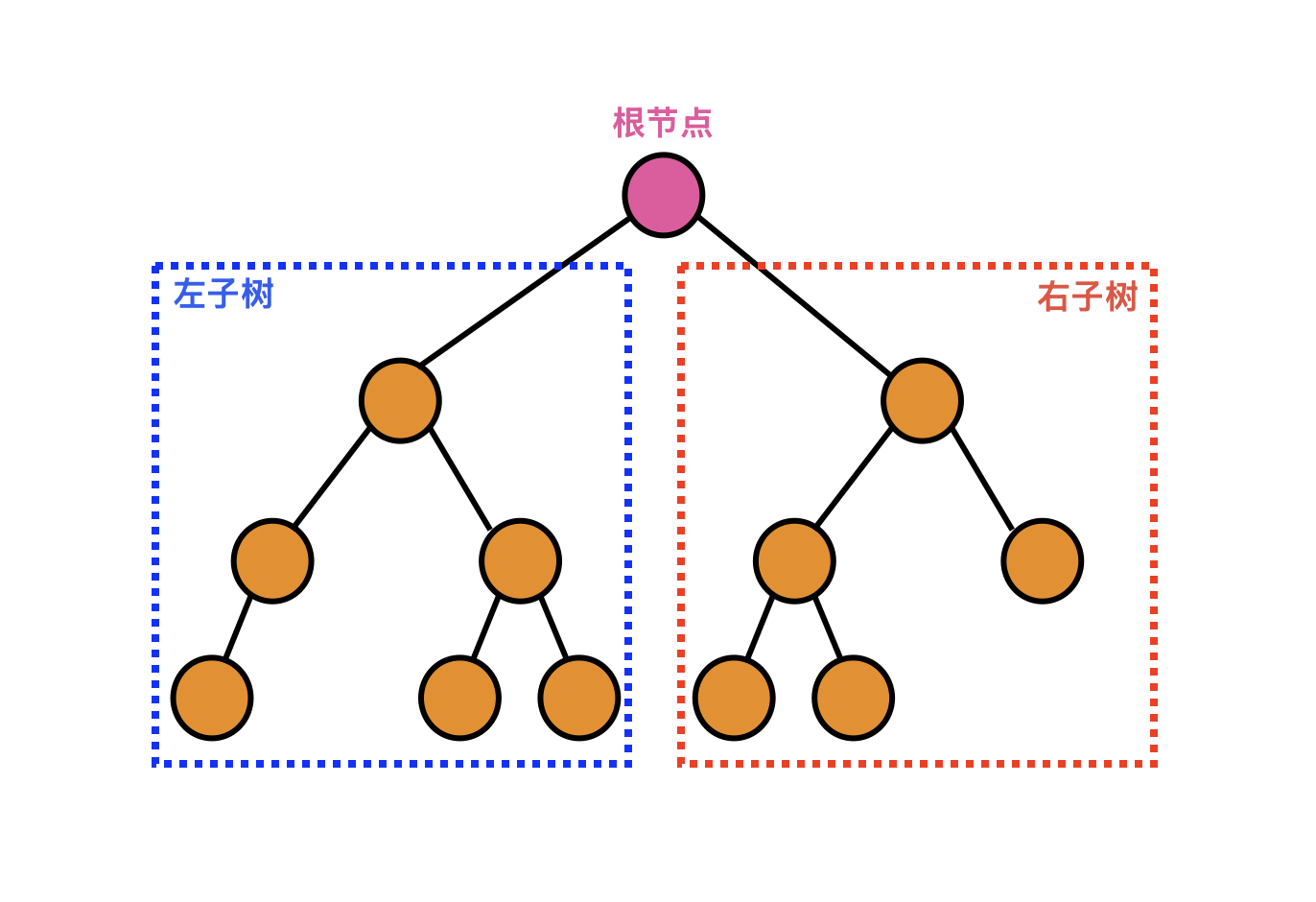
1. 二叉树中，每个结点的度都不大于2
2. 二叉树是有序树，左右子树有次序之分，不能颠倒

2.2.特殊的二叉树

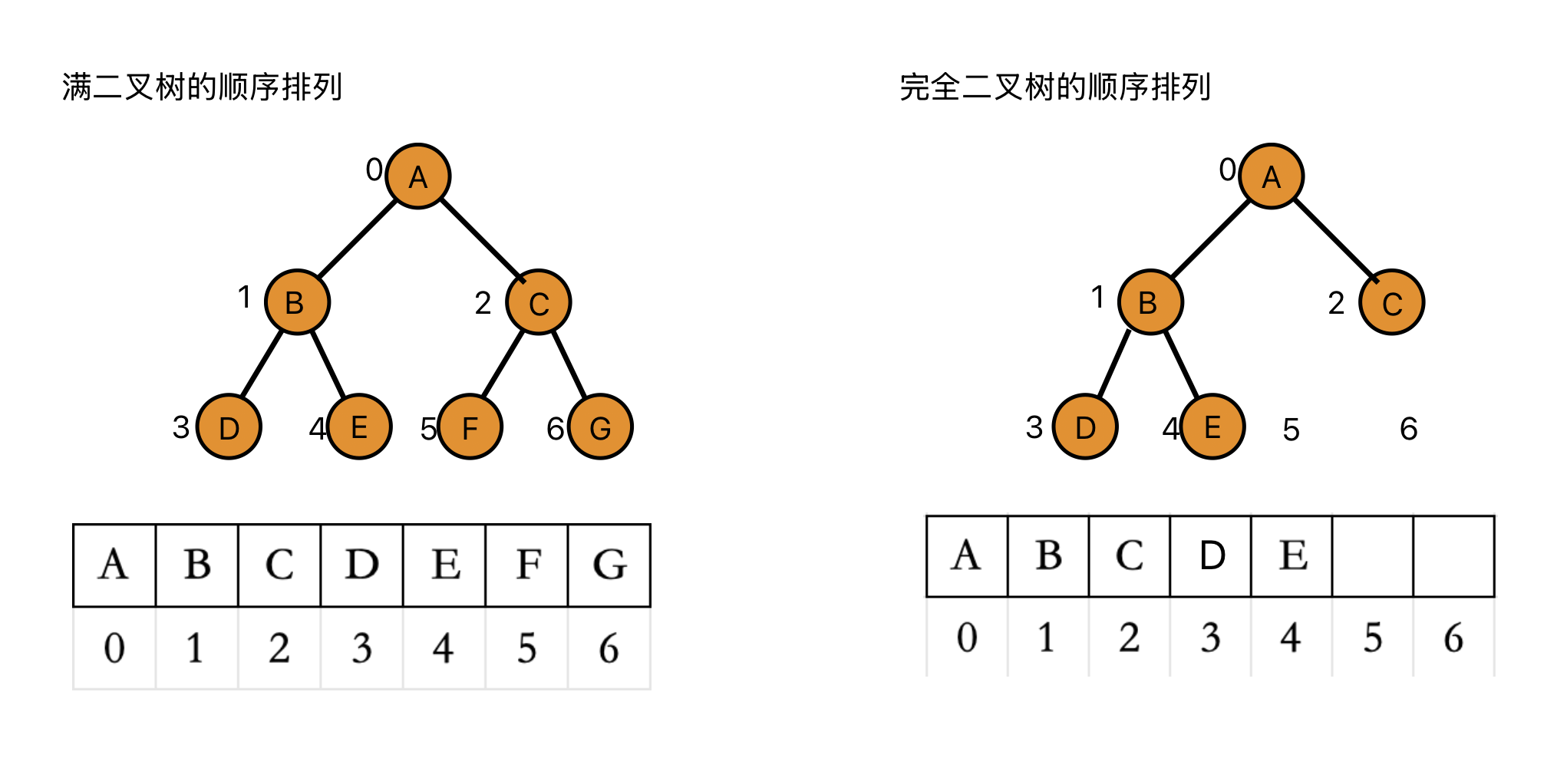
2.2.1.满二叉树

若一个二叉树中，每一层结点数都达到了最大值，那么这棵树就是满二叉树，假设层数为k，那么总结点个数为$2^k-1$

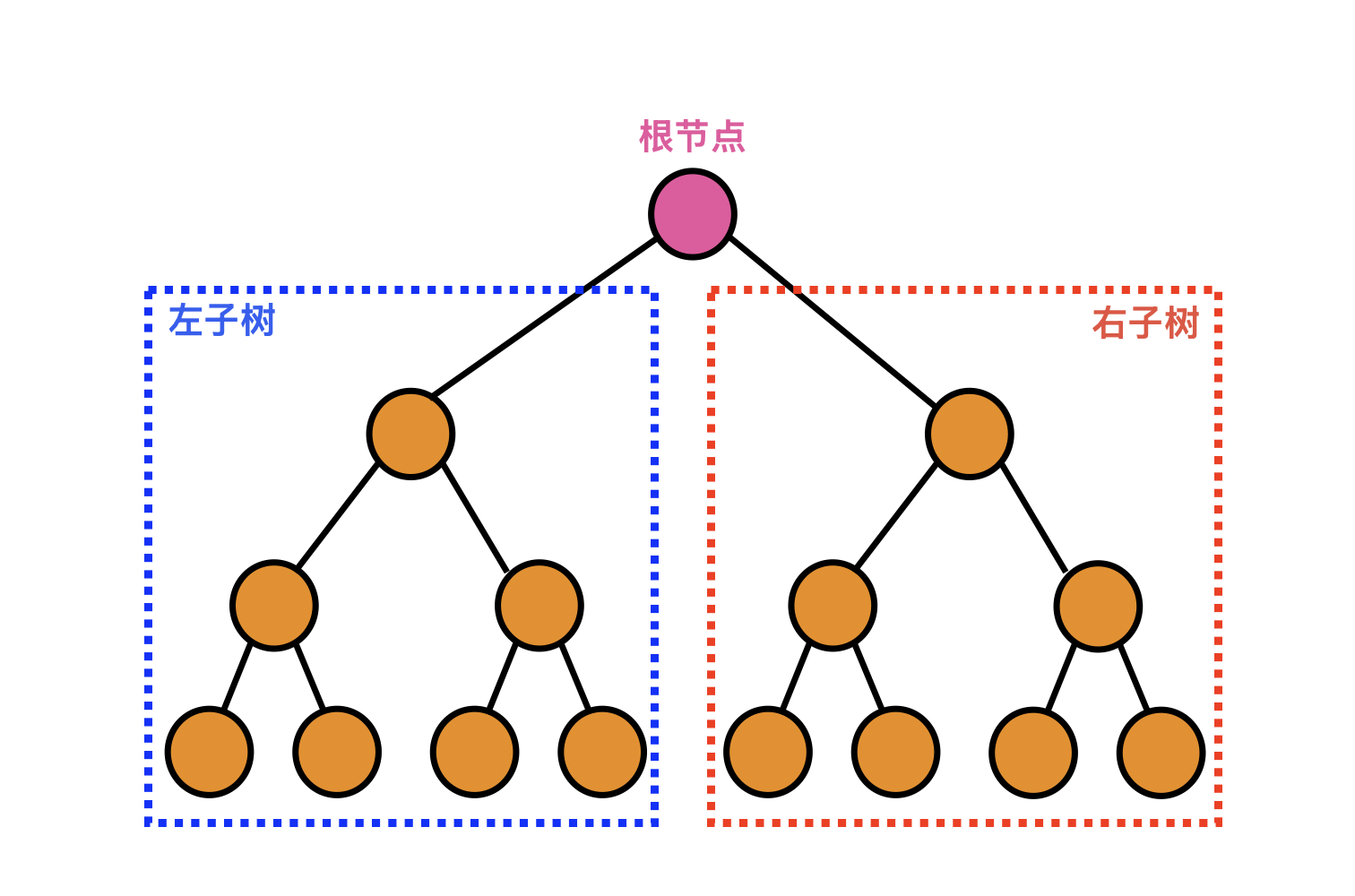
2.2.2.完全二叉树

完全二叉树是由满二叉树得来的，最后一层的结点个数不一定达到最大，其他层结点个数都到达最大值，且结点从左到右排列

2.3.二叉树的特性

规定根结点的层数为1:

1. 二叉树第i层上最多有$2^{i-1}$个结点
2. 深度为k的二叉树，最多有$2^k$个结点
3. 结点个数为n的满二叉树，它的深度为$lo{g}_2(n+1)$

2.4.二叉树的存储结构

一般分为顺序存储和链式存储两种

2.4.1.顺序结构

即用数组(顺序表)按顺序存储每一个节点

2.4.2.链式结构

用链表来表示二叉树，每一个节点都包含两个指针，分别指向自己的左孩子结点和右孩子结点，若该节点没有对应的孩子结点，则对应的指针为空

3.堆

3.1.堆的概念

大根堆/大堆/最大堆：把数据按照顺序存储的方式存储到一个完全二叉树中，其中根结点最大，每个结点的左右结点都不大于它本身，这样的存储结构就叫大根堆
小根堆/小堆/最小堆：把数据按照顺序存储的方式存储到一个完全二叉树中，其中根结点最小，每个结点的左右结点都不小于它本身，这样的存储结构就叫小根堆

假设根节点序号为0，节点总数为n(n>0)，取任意结点序号为i,则
左孩子序号=2i+1(<n)，若结果大于等于n，则该结点没有左孩子
右孩子序号=2i+2(<n)，若结果大于等于n，则该结点没有右孩子

3.2.堆的实现

3.2.1.堆结构的定义

由于堆是按照顺序存储方式存储的，所以结构体中的成员要包含一个数组(指针)、有效数据个数、数组的空间大小

//堆的结构
typedef int HPDataType;
struct Heap{HPDataType* arr;int size;//有效数据个数int capacity;//空间大小
}HP;

3.2.2.堆的初始化

把所有成员置为空即可

void HPInit(HP* php)
{assert(php);php->arr = NULL;php->size = php->capacity = 0;
}

3.2.3.堆的销毁

释放数组，把成员都置为空即可

void HPDestroy(HP* php)
{assert(php);free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}

3.2.4.插入数据

3.2.4.1.向上(下)调整算法

由于插入数据后，会破坏堆的平衡，因此我们要创建一个函数，用来调整堆中的数据位置，使堆再次保持平衡

向上调整算法：以创建小堆为例，从当前节点开始，与它的父节点比较，如果它小于父节点，那么与父节点交换位置，继续从他的父节点重复该操作，直到遇到根节点或当前节点不小于父节点为止
交换数据函数：

void swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}

向上调整算法：

//logn
void AjustUp(HPDataType* arr, int child)
{//一直向上比较并调整 直到遇到根节点while(child > 0){//计算父节点int parent = (child - 1)/2;//比较//建小堆 <//建大堆 >if(arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);child = parent;}else{break;}}
}

向下调整算法：以创建小堆为例，从根节点开始，与左右孩子中最小的比较，若根节点大于它，则跟它交换位置，并从该孩子节点继续重复以上操作，直到当前节点下标超出节点总数或左右孩子结点都不小于它为止

//logn
void AJustDown(HPDataType* arr, int parent, int n)
{//计算左孩子节点下标int child = parent * 2 + 1;//判断孩子节点是否越界while(child < n){//建小堆：找小孩子//建大堆：找大孩子//存在右孩子且比左孩子小(大) 则更新孩子节点if(child+1<n && arr[child]>arr[child+1]){child++;}//建小堆：<//建大堆：>if(arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent*2+1;}else{break;}}
}

3.2.4.2.插入数据

在数组末尾插入数据，再用向上调整算法使堆平衡即可

void HPPush(HP* php, HPDataType x)
{assert(php);//空间不够 扩容if(php->capacity == php->size){int newCapacity = php->capacity==0 ? 4 : 2*php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, sizeof(HPDataType)*newCapacity);//扩容失败if(tmp == NULL){perror("Realoc Failed!");exit(1);}php->arr = tmp;php->capacity = newCapacity;}php->arr[php->size++] = x;//向上调整AjustUp(php->arr, php->size-1);
}

3.2.5.堆的判空

判断size是否等于0即可

bool HPEmpty(HP* php)
{return php->size == 0;
}

3.2.6.删除(堆顶)数据

先判断堆是否为空，若不为空，交换堆顶数据与数组末尾数据的位置，size–，再用向下调整算法使堆平衡即可

void HPPop(HP* php)
{assert(!HPEmpty(php));swap(&php->arr[0], &php->arr[php->size-1]);--php->size;AJustDown(php->arr, 0, php->size);
}

3.2.7.取堆顶数据

若堆不为空，返回数组第一个元素即可

HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}

3.2.8.堆的数据个数

返回size值即可

int HPSize(HP* php)
{return php->size;
}

3.3.完整代码

Heap.h

//
//  Heap.h
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>//堆的结构
typedef int HPDataType;
typedef struct Heap{HPDataType* arr;int size;//有效数据个数int capacity;//空间大小
}HP;//初始化
void HPInit(HP* php);
//销毁
void HPDestroy(HP* php);//交换
void swap(HPDataType* a, HPDataType* b);
//向上调整算法
void AjustUp(HPDataType* arr, int child);
//向上调整算法
void AJustDown(HPDataType* arr, int child, int n);//插入数据
void HPPush(HP* php, HPDataType x);//判空
bool HPEmpty(HP* php);//删除数据
void HPPop(HP* php);//取堆顶元素
HPDataType HPTop(HP* php);//数据个数
int HPSize(HP* php);//打印堆
void HPPrint(HP* php);

Heap.c

//
//  Heap.c
#include "Heap.h"void HPInit(HP* php)
{assert(php);php->arr = NULL;php->size = php->capacity = 0;
}
void HPDestroy(HP* php)
{assert(php);free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}void swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}
//logn
void AjustUp(HPDataType* arr, int child)
{//一直向上比较并调整 直到遇到根节点while(child > 0){//计算父节点int parent = (child - 1)/2;//比较//建小堆 <//建大堆 >if(arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);child = parent;}else{break;}}
}
//logn
void AJustDown(HPDataType* arr, int parent, int n)
{//计算左孩子节点下标int child = parent * 2 + 1;//判断孩子节点是否越界while(child < n){//建小堆：找小孩子//建大堆：找大孩子//存在右孩子且比左孩子小(大) 则更新孩子节点if(child+1<n && arr[child]>arr[child+1]){child++;}//建小堆：<//建大堆：>if(arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent*2+1;}else{break;}}
}void HPPush(HP* php, HPDataType x)
{assert(php);//空间不够 扩容if(php->capacity == php->size){int newCapacity = php->capacity==0 ? 4 : 2*php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, sizeof(HPDataType)*newCapacity);//扩容失败if(tmp == NULL){perror("Realoc Failed!");exit(1);}php->arr = tmp;php->capacity = newCapacity;}php->arr[php->size++] = x;//向上调整AjustUp(php->arr, php->size-1);
}bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}void HPPop(HP* php)
{assert(!HPEmpty(php));swap(&php->arr[0], &php->arr[php->size-1]);--php->size;AJustDown(php->arr, 0, php->size);
}HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}
int HPSize(HP* php)
{return php->size;
}void HPPrint(HP* php)
{for(int i = 0; i < php->size; i++)printf("%d ", php->arr[i]);printf("\n");
}

main.c

//
//  main.c
#include "Heap.h"
void test(void)
{//建小堆HP hp;HPInit(&hp);HPPush(&hp, 29);HPPush(&hp, 17);HPPush(&hp, 14);HPPush(&hp, 31);HPPush(&hp, 22);HPPush(&hp, 12);HPPrint(&hp);printf("size: %d, top: %d\n", HPSize(&hp), HPTop(&hp));int k = 5;while(k--){HPPop(&hp);HPPrint(&hp);printf("size: %d, top: %d\n", HPSize(&hp), HPTop(&hp));}HPDestroy(&hp);HPPrint(&hp);
}
int main(void)
{test();return 0;
}

3.4.运行结果