文章目录
- 1. 神经网络基础
- 1.1 感知器(Perceptron)
- 1.2 深度神经网络(DNN)
- 2. 卷积神经网络(CNN)
- 2.1 核心思想
- 2.2 典型结构
- 2.3 ⾥程碑模型:
- 2.4 卷积层 - CNN 核心
- 2.5 池化层
- 3. 循环神经网络(RNN)
- 3.1 传统序列架构
- 核心思想
- 原始 RNN 的局限性
- RNN 优化
- 3.2 编码器-解码器架构
- 4. 词嵌入算法
- 4.1 基本概念
- 4.2 解决问题
- 4.3 嵌入矩阵
- 4.4 词嵌入模型
- 4.5 词嵌入算法
1. 神经网络基础
1.1 感知器(Perceptron)
- 符号主义称之为感知机,连接主义称之为神经元
- f(n)={0,w1x1+w2⋅x2≤θ1,w1x1+w2⋅x2>θf(n) = \begin{cases} 0, & w_1x_1+ w_2\cdot x_2 \le \theta \\ 1, & w_1x_1+ w_2\cdot x_2 \gt \theta \end{cases}f(n)={0,1,w1x1+w2⋅x2≤θw1x1+w2⋅x2>θ
- 单层感知机:简单逻辑门(AND, NAND, OR)
- 多层感知机:NOR
1.2 深度神经网络(DNN)
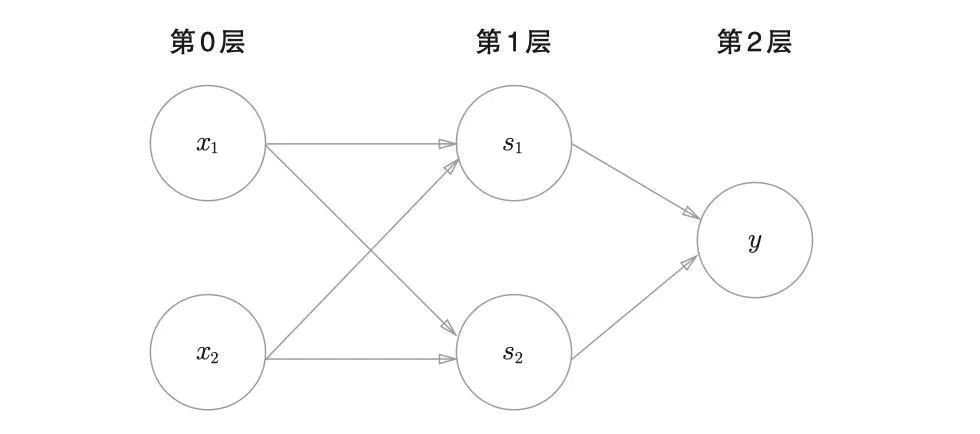
- 组成:神经网络由输入层、隐藏层和输出层组成,每层包含多个神经元
- 训练过程:主要包括前向传播、损失计算和反向传播三个步骤
- 前向传播
- 输入层:输入原始数据,假设有两个神经元,a(0)=[x0,x1]Ta^{(0)}=[x_0, x_1]^Ta(0)=[x0,x1]T
- 隐藏层:z(1)=W1⋅a(0)+b(1),a(1)=g1(z(1))z^{(1)} = W^{1}⋅a^{(0)}+b^{(1)}, a^{(1)} = g_1(z^{(1)})z(1)=W1⋅a(0)+b(1),a(1)=g1(z(1)) , g 是任意的激活函数
- 输出层,z(2)=W2⋅a(1)+b(2),a(2)=g2(z(2))z^{(2)} = W^{2}⋅a^{(1)}+b^{(2)}, a^{(2)} = g_2(z^{(2)})z(2)=W2⋅a(1)+b(2),a(2)=g2(z(2))
- 损失函数
- 回归任务:均方误差(MSE)-> 计算预测值与真实值的平方差的平均值
- 分类任务:交叉熵损失,二分类或多分类 -> 衡量两个概率分布(预测分布$ \hat y $与真实分布y)的差异
- 代价函数
- 代价函数是训练集上所有样本损失的平均值,用于衡量模型在整体数据上的表现
- J(W,b)=1m∑i=1mL(yi^,yi)+λ⋅R(W)J(W,b) = \frac{1}{m}\sum_{i=1}^{m}L(\hat{y_i}, y_i) + \lambda\cdot{R(W)}J(W,b)=m1∑i=1mL(yi^,yi)+λ⋅R(W),λ\lambdaλ 为惩罚系数,正则项 R(W) 又称惩罚项,常用L1、L2正则。
- 反向传播
- 利用链式法则计算代价函数对各层权重 W 和偏置 b 的梯度,并通过梯度下降法更新参数,最终减小化代价函数。
- 前向传播
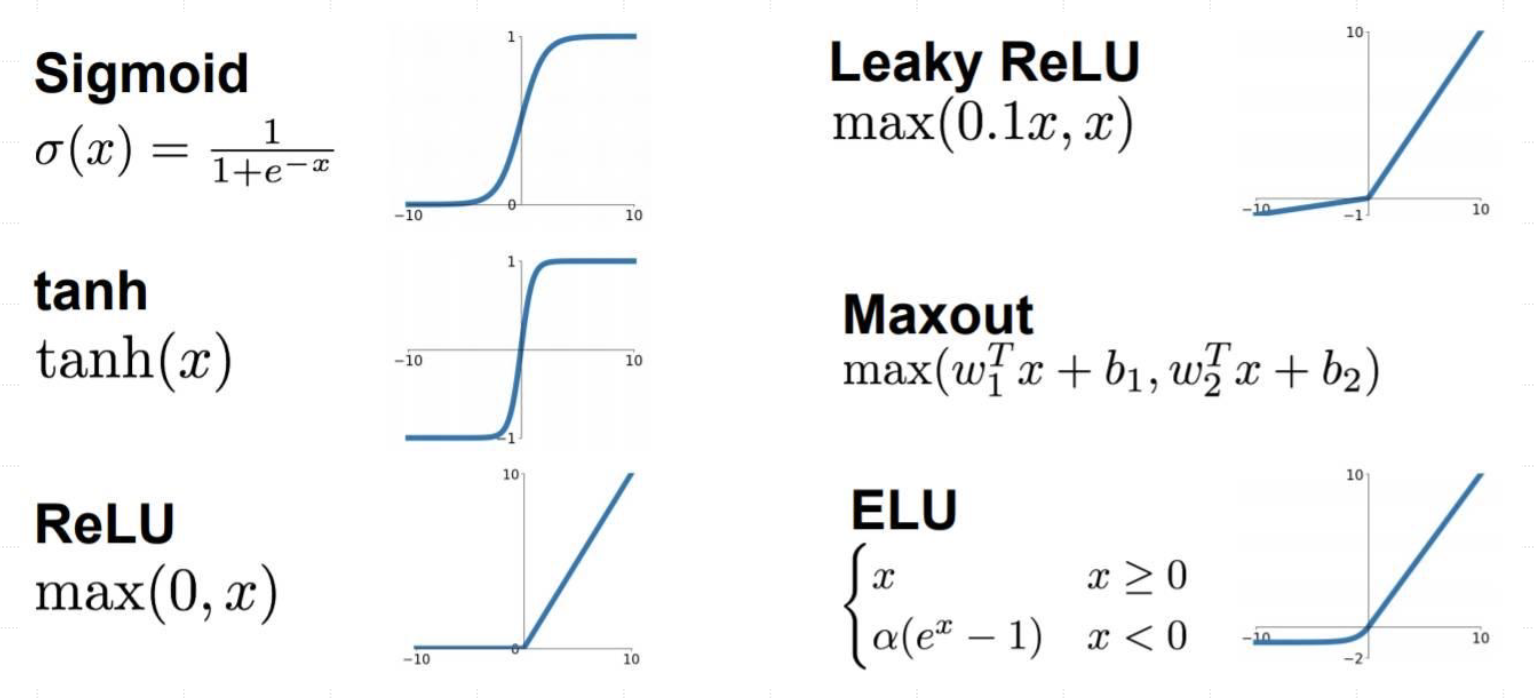
- 激活函数是神经网络的重要组成部分,它们决定了神经元如何将输入信号转换为输出信号,可以用于学习非线性关系
2. 卷积神经网络(CNN)
2.1 核心思想
- 利⽤卷积层和池化层构建层级化的特征提取器。
2.2 典型结构
- 输⼊ -> [ [卷积层 -> 激活函数] x N -> 池化层? ] x M -> [ 全连接层 -> 激活函数 ] x K -> 输出层
2.3 ⾥程碑模型:
- LeNet-5 (1998): 卷积⽹络的早期成功应⽤(手写数字识别),奠定基础结构。
- AlexNet (2012): ImageNet 竞赛冠军,引爆深度学习⾰命。关键贡献:更深的⽹络、ReLU、Dropout、GPU 加速。
- VGGNet (2014): 探索深度影响。使⽤⼩的 (3x3) 卷积核堆叠,结构简洁,证明深度是关键。
- GoogLeNet / Inception (2014): 引⼊ Inception 模块,实现“网络中的网络”,在增加深度和宽度的同时控制计算成本。
- ResNet (2015): 引⼊残差连接 (Residual Connection),解决了深度⽹络训练中的梯度消失/退化问题,使构建数百甚⾄上千层⽹络成为可能。
2.4 卷积层 - CNN 核心
- ⼯作原理
- 使⽤卷积核 (Kernel) 在输入数据(如图像)上滑动,提取局部特征。
输入矩阵边缘处理:填充 0 -> 宽卷积 v.s. 窄卷积
- 关键特性
- 参数共享: 同⼀个卷积核在整个输入上共享权重,极大减少参数量。
- 局部连接:神经元只与输入的⼀个局部区域连接。
- 平移不变性: 对特征的位置不敏感。
- 主要参数
- 卷积核大小
- 步长 (Stride)
- 填充 (Padding)
- 通道数
2.5 池化层
- 目的
- 降维、减少计算量
- 增强特征鲁棒性 (对微小位移不敏感)
- 作用
- 逐步减小特征图的空间尺寸,增大感受野。
- 常见类型
- 最大池化 (Max Pooling): 取区域内的最大值。
- 平均池化 (Average Pooling): 取区域内的平均值。
3. 循环神经网络(RNN)
3.1 传统序列架构
核心思想
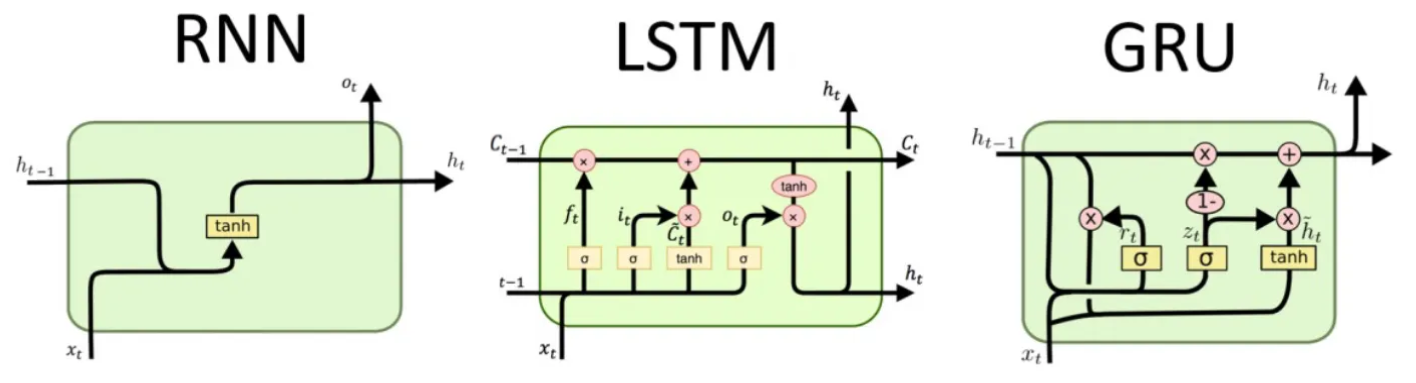
- 处理序列数据(文本、语音、时间序列),利用隐藏状态传递历史信息。
原始 RNN 的局限性
- 难以捕捉长期依赖 (梯度消失/爆炸问题)。
RNN 优化
- LSTM (Long short-Term Memory)
- 通过精密的门控单元(遗忘门、输入门、输出门)和细胞状态 (Cell state),有效控制信息的长期记忆和遗忘。
- GRU (Gated Recurrent Unit)
- 结构比 LSTM 简单(只有更新门、重置门),参数更少,在许多任务上表现与 LSTM 相当。
3.2 编码器-解码器架构
序列到序列模型 (Seq2Seq)
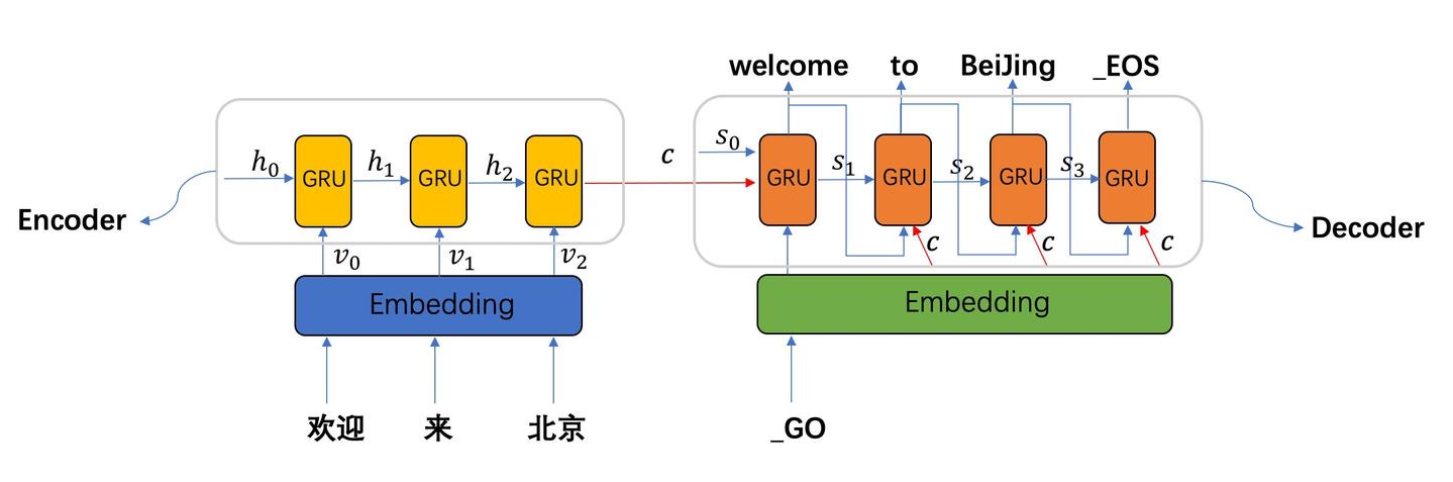
- 典型应用: 序列到序列(Seq2Seq)任务,如机器翻译
- 结构组成:
- 编码器: 将输入序列编码为固定长度向量
- 解码器: 基于编码向量生成输出序列
- 工作流程: 如"欢迎来北京"→"welcome to Beijing"的翻译过程
- 实现方式: 通常使用 GRU 或 LSTM 作为基础单元
4. 词嵌入算法
4.1 基本概念
词嵌入是自然语言处理(NLP)中用于将文本中的 “词” 转换为低维稠密向量的技术,核心目标是用数值向量表示词的语义信息。在神经网络中,嵌入层(Embedding Layer)的功能就是通过嵌入矩阵将词的索引转换为嵌入向量
4.2 解决问题
传统方法(如 one-hot 编码)只能将文本转化为离散稀疏向量,实现简单但存在维度灾难和语义鸿沟(无法描述词与词之间的语义关联)等问题。
4.3 嵌入矩阵
嵌入矩阵是存储所有词嵌入的参数矩阵,是词嵌入技术的核心数据结构
- 存储与查询:嵌入矩阵本质是一个查找表,通过词的索引(one-hot编码)可直接获取对应的嵌入向量(如词汇表中 “猫” 的索引是 0,则嵌入向量为 W [0,:]);
- 参数学习:嵌入矩阵是模型的可学习参数,通过训练数据(如大规模文本)迭代优化,最终使向量满足语义相关性等特性(初始化时通常为随机值,通过反向传播更新)。
4.4 词嵌入模型
- Skip-Gram 模型
- CBOW 模型
4.5 词嵌入算法
- word2vec (本质是一个softmax多标签分类)
- Glove




)














