本节主要讲的是模型训练时的算法设计
数据预处理:
关于数据预处理,我们有常用的3个符号,数据矩阵X,假设其尺寸是,N是数据样本的数量,D是数据的维度
均值减法(Mean subtraction):
是预处理最常用的形式,它对数据中每个独立特征减去其该独立特征在所有样本中的平均值
对于图片来说,更常见的时对所有像素都减去所有像素值的平均值,也可以在3个颜色通道上分别操作
归一化(Normalization):
指将数据的所有维度都归一化,使其数值范围都近似相等
这个操作的意义在于当不同维度的输入特征具有不同的数值范围(或计量单位)且差异较大时,可以避免传播时部分特征相关的权重的梯度过大
在图像处理中,由于像素的数值范围几乎是一致的,所以额外进行这个预处理步骤就显得没有那么必要
归一化的两种方法:
第一种方法:
对数据做0中心化处理,然后对每个维度都除以其维度对应的标准差
即
其中S为X的标准差
第二种方法:
对每个维度都做归一化,使得每个维度的最大值和最小值是1和-1
即
PCA与白化(Whitening):
我们可以对协方差矩阵进行SVD(奇异值分解),并利用奇异值分解来减小数据矩阵的size
这里先来复习一下SVD
SVD的描述如下:
奇异值:
设是秩为r的
的矩阵,则
是对称矩阵且可以正交对角化,则
的特征值
,设对应的特征向量为
, 则规定奇异值
,且
奇异值分解:
矩阵A同上,那么存在一个矩阵,其中D的对角元素是A的前r个奇异值,满足排序
,且存在一个
的正交矩阵U和一个
的正交矩阵V,使得
其中
是U的第i个列向量,当m>n时,多余的u自行补充单位向量,使U满足正交矩阵
和上面提到的意义一致,构成V的第i个列向量
PCA过程:
原理:
设表示以
为样本观测值的是随机变量,如果能找到
,使得
的值达到最大,就表明了这m个变量的最大差异,当然需要规定
,否则Var可以是无穷大
这个解是m维空间的一个单位向量,代表一个方向,称之为主成分方向
一般来说代表原来m个变量的主成分不止一个,但不同主成分信息之间不能相互包含,即两个主成分的协方差应为0
即:
设表示第i个主成分
则要使
达到最大,又要有
与
垂直,且使
达到最大,以此类推,至多可以得到m个主成分
步骤:
1.先对数据进行0中心化处理,然后计算协方差矩阵R(这里也是相关系数矩阵),假设size为
R的第(i,j)个元素是第i个维度和第j个维度的协方差,所以可以知道,这个矩阵是一个方阵,且是对角矩阵,且对角线上的元素,比如第(i,i)个元素,恰好是第i维特征的方差。且该矩阵是半正定矩阵
2.计算出R的特征值,以及对应的标准正交化特征向量
,其中
则得到m个主成分,第i个主成分为
,其中
已经被归一化了
3.计算前j个主成分的累计贡献率:
取定贡献率一个阈值,比如75%,进而解得j,从而确定保留j个主成分
4.最后我们保留j个主成分代替之前的m个X进行分析即可,也就是把维度m降低到了j
实际计算中,我们常用SVD代替步骤2的特征分解(计算效率更高),也就是先对数据矩阵进行标准化,然后直接对数据矩阵D进行SVD分解(跳过计算协方差矩阵这一步),然后用SVD的V里的替代上文的
,
就取
的
,假设最后保留j个主成分,其对应的向量为
,则降维后的矩阵变成
优点:
通常使用PCA降维后的数据训练神经网络的性能会更好,同时节省时间和储存器空间
白化:
目的是为了让数据具有以下特性:
1.均值为0,数据分布的中心在原点
2.单位协方差,所有维度的方差为1
3.无相关性,不同维度之间完全独立,协方差为0
步骤:
1.中心化,减去均值
2.计算协方差矩阵
3.对协方差矩阵进行特征值分解
4.对每个维度除以其特征值的平方根,在除的时候,为了防止分母为0,需要添加一个小常量
PCA与白化通常不用于卷积神经网络
预处理重要规则:
对于训练集/验证集/测试集,我们在中心化的时候,只采用集合内有的样本所产生的统计特征量进行预处理,比如,对训练集进行预处理的时候,只用训练集的均值/方差;对验证集、测试集同理
权重初始化:
小随机数初始化:
由于数据经过了恰当的归一化处理,可以假设所有权重数值大约一半为正数,一半为负数,则其期望应为0,但又不能全为0,因为神经元之间是不对称的,所以,我们可以将权重初始化为小的数值,随机且不相等,通常的随机是从基于0均值和标准差为1的高斯分布中生成随机数。但不是小数值就一定会得到好的结果,因为这样会导致反向传播时出现非常小的梯度,从而很大程度地减小反向传播中的梯度信号
使用 来校准方差
上述的做法存在一个问题,随着输入数据量的增大,随机初始化神经元的输出数据分布中的方差也在增大,因此,我们需要将其除以输入数据量的平方根,来调整其方位,使其输出的方差归一化到1
证明过程如下:
第三个等号到第四个等号用到了
所以,如果想要s和x有一样的方差,就需要满足,又我们之前是由标准差为1的高斯分布随机取得w,所以
,所以我们只要令
即可
稀疏初始化(Sparse initialization):
将所有权重矩阵设为0,但为了打破对称性,每个神经元都要与下一层固定数目(经典连接数目是10个)的神经元随机连接(权重由小的高斯分布生成)
偏置的初始化:
通常将偏置初始化为0,这是因为随机数权重矩阵已经打破了对称性,对于ReLU非线性激活函数,有人喜欢用0.01这样的小数值常量作为所有偏置的初始值,认为这样做能够使所有的ReLU单元一开始就激活
批量归一化(Batch Normalization):
核心思想是在网络的每一层(尤其是全连接层/卷积层之后,激活函数之前),对输入数据进行标准化处理,使其在训练过程中保持相对稳定的分布,从而缓解梯度消失/爆炸,提高对初始化和学习率的鲁棒性
步骤:
假设我们有一个mini_batch的数据输入,size为m,对于每个神经元的输入,我们都计算mini_batch的均值以及方差,并利用这个均值与方差对输入进行标准化
正则化(Regularization):
控制神经网络过拟合的方法之一
L2正则化:
对每个权重w,我们都向Loss中添加一项,系数为
是因为这样子梯度的系数就为1了,L2正则化的直观理解是它对大数值的权重向量进行严厉的乘法,倾向于更加分散的权重向量,使网络更倾向于使用所有输入特征,而不是严重依赖于输入特征中的某些小部分特征
使用L2正则化意味着所有的权重梯度都会有一个以的线性下降的方向成分
L1正则化:
对每个w我们向Loss加入,L1正则化会让权重向量在最优化的过程中变得稀疏(非常接近0),也就是说使用L1正则化后,神经元更倾向于使用输入数据中最重要特征所构成的稀疏子集,同时对噪声的输入不敏感。
一般来说L2正则化的效果要优于L1正则化
最大范氏约束(Max norm constraints)
另一种形式的正则化,给每个神经元的权重向量的量级设定上限,并使用投影梯度下降来确保这一约束,即,其中c为常数,一般为3或4,这种正则化有一个好处,在学习率设置过高的时候,网络中也不会出现数值爆炸,因为参数更新始终被限制
随机失活(Dropout):
非常简单且有效的正则化方法
实现方法:在训练时,让神经元以p(超参数)的概率被激活或者设置为0(失活)
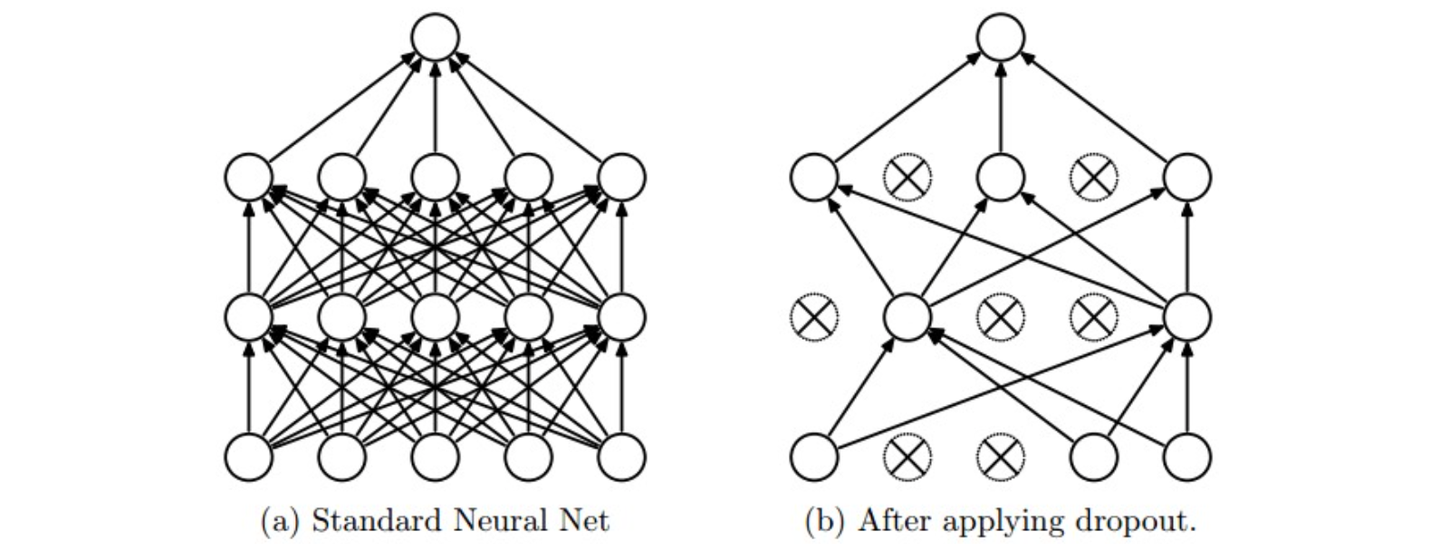
在训练过程中,可以认为是对完整的神经网络中抽样出一些子集,每次基于输入数据只更新子网络的参数(但子网络并不是相互独立的,它们都共享参数)
在测试过程中,不再使用随机失活,而是使用整个神经网络进行预测,可以理解为对数量巨大的子网络做了模型集成(model ensemble),从而计算出一个平均的预测
前向传播中的噪声:
Dropout属于网络在前向传播中具有随机行为的方法,则会对真实分布产生一定的噪声,可以通过分析法、数值法将噪声边缘化
分析法:
由于Dropout只在训练时进行随机失活,导致每个神经元对其接受的输入x的期望是px。则在预测的时候,不再随机失活,为了保证神经元能够复现之前训练的环境,来保证其预测的正确性,需要将其接受的每个输入x乘上一个系数p,从而保证同样的预测期望输出
数值法:
抽样出很多的子网络,随机选择不同的子网络进行前向传播,最后对他们的预测取平均值
损失函数:
属性分类:
之前讲到的损失公式的前提,都是假设每个样本只有一个正确的标签,但如果每个样本都可以有或没有多个标签,且标签之间互不排斥呢?
这种情况下,我们需要为每个属性创立一个独立的二分类的分类器,并都对其采用一个Loss函数,最后将这多个Loss函数求和
或者,我们可以对每种属性训练一种独立的逻辑回归分类器



顾客管理、供应商管理、用户管理)


 流媒体解决方案)



CA1区域(vCA1)的混合调谐细胞(mixed-tuning cells)对NLP中的深层语义分析的积极影响和启示)

)


: 阴影(shadowMap,PCF,PCSS))


![[STM32][HAL]stm32wbxx 超声波测距模块实现(HY-SRF05)](http://pic.xiahunao.cn/[STM32][HAL]stm32wbxx 超声波测距模块实现(HY-SRF05))
