Problem Statement

You are given a simple connected undirected graph G with N vertices and M edges.
The vertices of G are numbered vertex 1, vertex 2, …, vertex N, and the i-th (1≤i≤M) edge connects vertices Ui​ and Vi​.

Find the lexicographically smallest simple path from vertex X to vertex Y in G.
That is, find the lexicographically smallest among the integer sequences P=(P1​,P2​,…,P∣P∣​) that satisfy the following conditions:

• 1≤Pi​≤N

• If ij, then Pi​Pj​.

• P1​=X and 

• For 1≤i≤∣P∣−1, there exists an edge connecting vertices Pi​ and Pi+1​.

One can prove that such a path always exists under the constraints of this problem.

You are given T test cases, so find the answer for each.

Lexicographic order on integer sequencesAn integer sequence S=(S1​,S2​,…,S∣S∣​) is lexicographically smaller than an integer sequence T=(T1​,T2​,…,T∣T∣​) if either of the following 1. or 2. holds. Here, ∣S∣ and ∣T∣ represent the lengths of S and T, respectively.

1. ∣S∣<∣T∣ and (S1​,S2​,…,S∣S∣​)=(T1​,T2​,…,T∣S∣​).

2. There exists some 1≤i≤min(∣S∣,∣T∣) such that (S1​,S2​,…,Si−1​)=(T1​,T2​,…,Ti−1​) and Si​<Ti​.

Constraints

• 1≤T≤500

• 2≤N≤1000

• N−1≤M≤min(2N(N−1)​,5×104)

• 1≤X,Y≤N

• XY

• 1≤Ui​<Vi​≤N

• If ij, then (Ui​,Vi​)(Uj​,Vj​).

• The given graph is connected.

• The sum of N over all test cases in each input is at most 1000.

• The sum of M over all test cases in each input is at most 5×104.

• All input values are integers.

---

Input

The input is given from Standard Input in the following format:

T
case1​
case2​
⋮
caseT​

casei​ represents the i-th test case. Each test case is given in the following format:

N M X Y
U1​ V1​
U2​ V2​
⋮
UM​ VM​

Output

Output T lines.
The i-th line (1≤i≤T) should contain the vertex numbers on the simple path that is the answer to the i-th test case, in order, separated by spaces.
That is, when the answer to the i-th test case is P=(P1​,P2​,…,P∣P∣​), output P1​, P2​, …, P∣P∣​ on the i-th line in this order, separated by spaces.

---

Sample Input 1

2
6 10 3 5
1 2
1 3
1 5
1 6
2 4
2 5
2 6
3 4
3 5
5 6
3 2 3 2
1 3
2 3

Sample Output 1

3 1 2 5
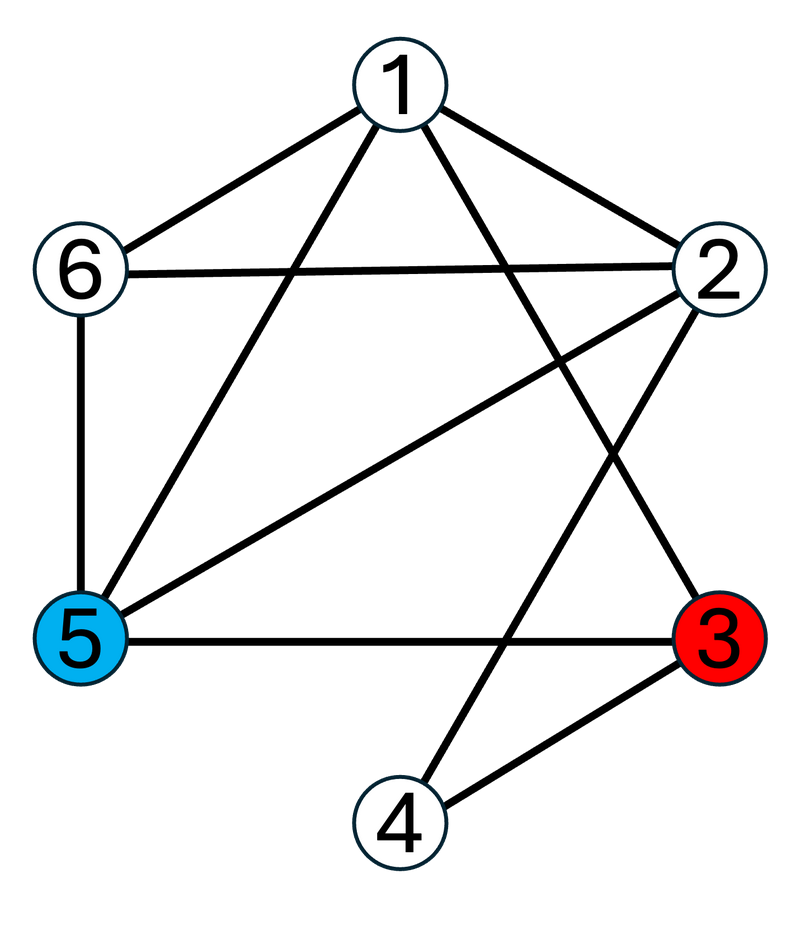
3 2

For the first test case, graph G is as follows:

The simple paths from vertex 3 to vertex 5 on G, listed in lexicographic order, are as follows:

• (3,1,2,5)
• (3,1,2,6,5)
• (3,1,5)
• (3,1,6,2,5)
• (3,1,6,5)
• (3,4,2,1,5)
• (3,4,2,1,6,5)
• (3,4,2,5)
• (3,4,2,6,1,5)
• (3,4,2,6,5)
• (3,5)

Among these, the lexicographically smallest is (3,1,2,5), so output 3,1,2,5 separated by spaces on the first line.

For the second test case, (3,2) is the only simple path from vertex 3 to vertex 2.

题目大意：找到从x到y的最小字典序通路

用邻接图存储，排序，dfs搜索，回溯，注意回溯的时候，不用把状态再改回false，因为我们在dfs到该点时，已经发现它是构不成连通的，所以下次就不需要再到达这个节点了，这样可以减少很大一部分运算，从而将TLE的代码变成AC

AC代码：

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const ll N=200010;
int n,m,x,y;
vector<int>path;
bool found;	
void dfs(int current,vector<vector<int>>&graph,vector<bool>&visit){path.push_back(current);visit[current]=true;if (current==y){found=true;for (int i:path)  cout<<i<<" ";cout<<"\n";return ;	}sort(graph[current].begin(),graph[current].end());for (auto i:graph[current]){if (!visit[i]&&!found){visit[i]=true;dfs(i,graph,visit);if (found)return ;path.pop_back();}}
}
void solve(){cin>>n>>m>>x>>y;vector<vector<int>>graph(n+1);for (int i=1;i<=m;i++){int u,v;cin>>u>>v;graph[u].push_back(v);graph[v].push_back(u);}path.clear();vector<bool>visit(n+1,false);found=false;dfs(x,graph,visit);
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--){solve();}
}