大家好,接下来,我将带来对于搜索篇的新内容,这部分我将打算围绕DFS深度优先搜索去讲解。
温馨提示:由于这篇文章是接着上一篇文章的,如果新读者没有看过前一篇的话,推荐去看一下,不然有些地方可能会不懂。
接下来的每道题我相信大家都会有所收获的!
1.题目概述:
这部分我将讲解以下有关DFS的题目
1.选数 --- P1036 [NOIP 2002 普及组] 选数 - 洛谷
2.飞机降落 --- P9241 [蓝桥杯 2023 省 B] 飞机降落 - 洛谷
3.八皇后 --- P1219 [USACO1.5] 八皇后 Checker Challenge - 洛谷
4.数独 --- P1784 数独 - 洛谷
这部分的题比上篇文章的题难度要提高挺多,大家可以如果有所困难可以多多思考一下。
2.选数

大家会发现,如果看了我前面的算法篇1的话其实很容易解决dfs递归的内容的。
但是大家会发现这里有一个新问题:如何求解一个数是不是素数呢?
这个的话有挺多的方法的,我在这里就用了一个简单的方法
比如判断一个数x是不是素数,由素数的定义我们可以知道:素数是大于1的正整数,而且只能被自己和1整除。
那么我们就可以从2开始到x所有的数拿去试除即可解决。
但是要判断的这些数有点多了,我们就可以去选择试除到根号x即可,具体的原因网上有证明,有兴趣的读者可以去看看。
(如果想判断大量数字是否为素数,可以采用埃拉托色尼筛选法)
大家在看题目,发现结果并不会因为数字的顺序不同而改变,所以是一种组合。
我们就得在dfs的参数中加入一个begin参数来表示从哪个数开始的
首先我们画一下这个决策树:
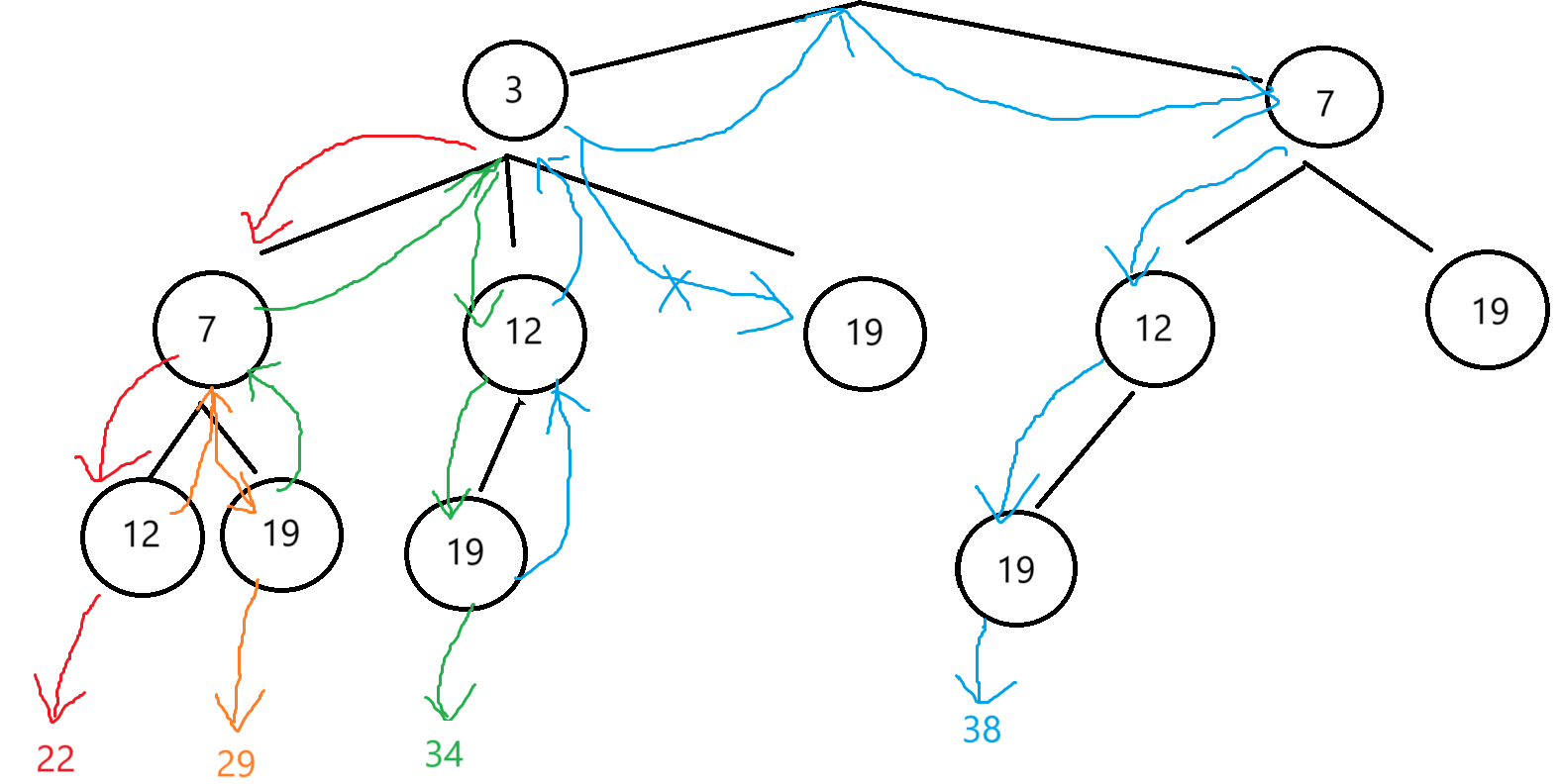
我们根据自己画的决策树就可以来写代码了:
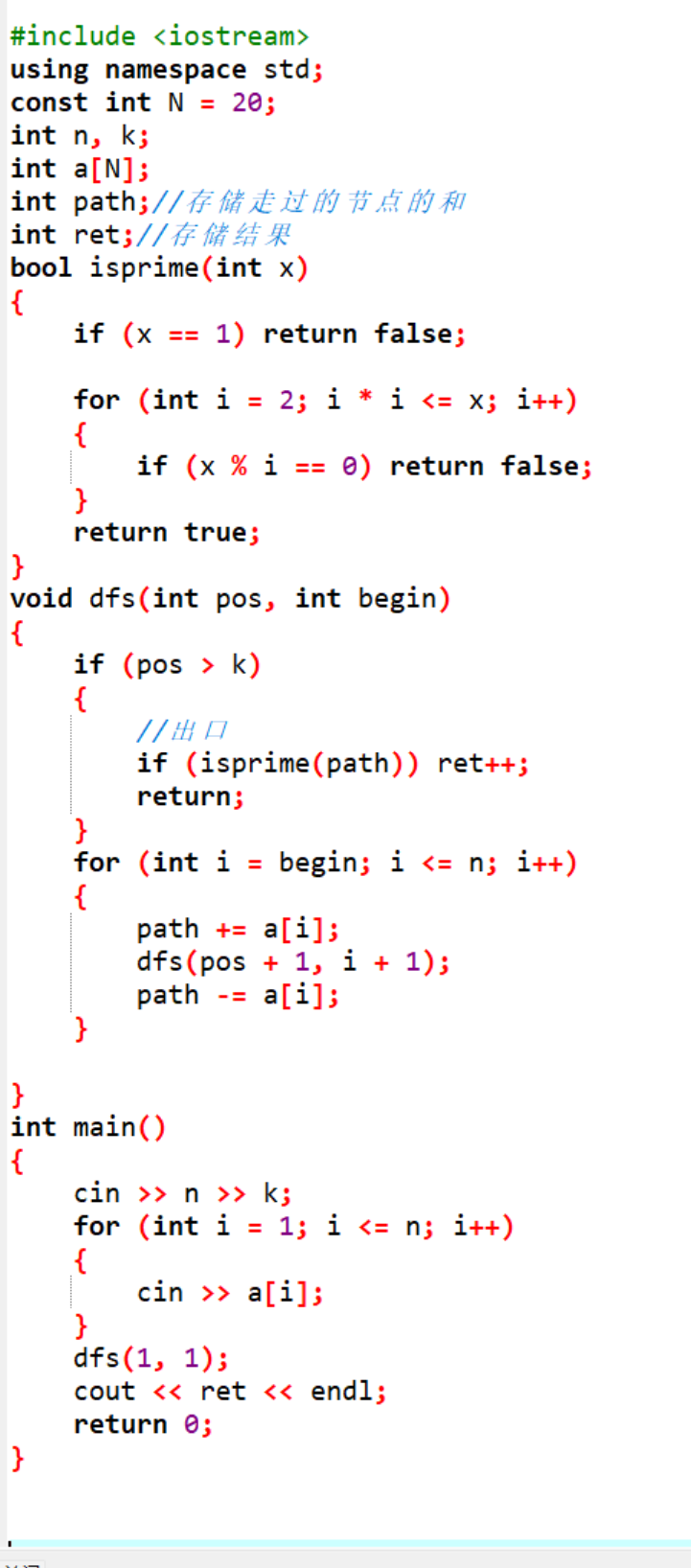
当然这道题跟上篇文章中的思路是一样的,回溯递归
3.飞机降落
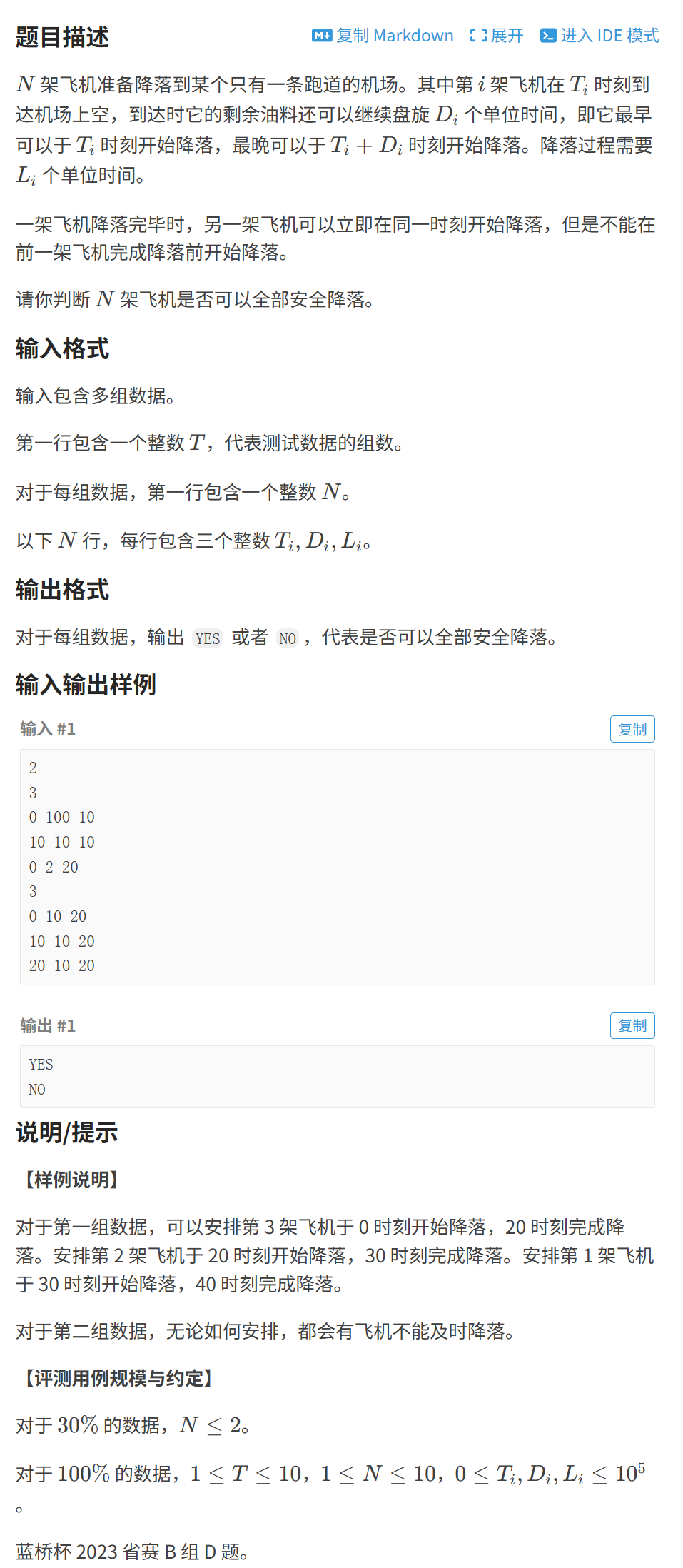
这道题的难度就比较高了,大家好好理解一下题目,可以尝试做一做
那跟着博主的思路一起来看一下这道题吧。
这道题会发现的是如果直接来做的话,要安排好每架飞机的顺序,保证该组飞机能够安全降落,那么如果怎么都安排不出来,就代表这个不能及时降落了。所以如何安排顺序就是我们的问题了,
我们这时候就可以通过搜索去枚举出来所有情况。而且数据也是比较小的,通过搜索去做也不会出现超时,很显然也在暗示我们去搜索。
由于这道题的枚举类似排列,所以我们就不需要一个begin值去告诉该从什么位置递归了。
对于安排过的飞机,我们只需要通过一个bool st[]数组去标记一下即可。
当遇到了标记过的飞机就直接剪掉这个分支。
上一架飞机结束时间需要记录一下,因为上一架飞机结束时间 > 新飞机到达时间 + 最长盘旋时间,就代表了新飞机无法降落,我们也将这个分支给剪掉。
那对于新飞机的结束时间怎么计算呢?
1.新飞机到达时间 >= 前一架飞机结束时间(新飞机到达的时间晚于前一架飞机的结束)
那么新飞机结束时间 = 新飞机的到达时间 + 新飞机的降落时间
2.新飞机到达时间 < 前一架飞机结束时间
比较一下
新飞机到达时间 + 盘旋时间 是否大于等于 前一架飞机结束时间
如果是 ----> 新飞机能正常降落 ---- 新飞机结束时间 = 前一架飞机结束时间 + 新飞机降落时间
如果不是 ---> 新飞机无法正常降落
所以新飞机的结束时间 = max(前飞机的结束时间, 新飞机到达时间) + 新飞机降落时间
根据博主的思路大家好好想想,将这个条件理解后,我们就可以来实现代码了。
读者可以先尝试写一下

这样就可以实现出这到题了
大家可以仔细理解一下。
4.八皇后

大家还是可以先自己做一下,看看有哪里不懂的。
接下来就跟着博主的思路来理一下这道题吧,我们看完这道题后,我们知道的是什么呢?
我们无非就是要往这个矩阵中填棋子,将解的个数输出即可。
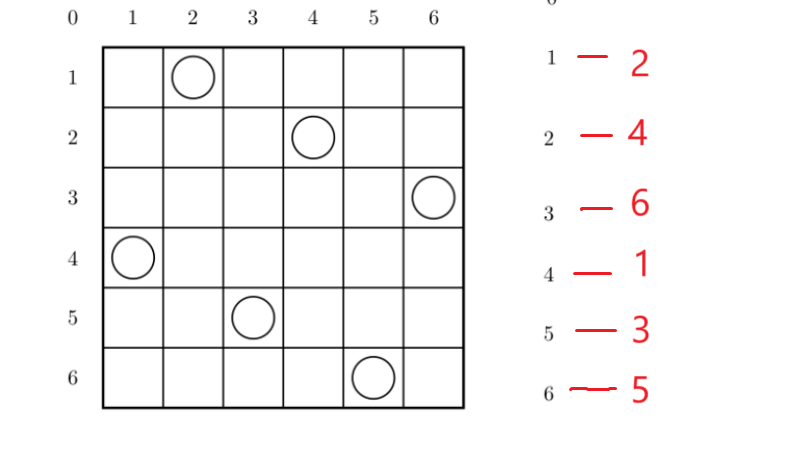
我们对应的布局就如下面这样
对应的246135数字都为对应的1,2,3,4,5,6行对应的列
所以我们有了对应的数字246135就可以得到对应的棋局布置了
我们可以发现数据并不是很大,我们就可以去尝试枚举所有的情况了,将所有棋子的填充情况都枚举一遍不就解决了吗?
我们要填数肯定也有对应的限制了,那么限制是什么呢?
题目有说:行、列、对角线至多只能有一个棋子
所以我们通过这个条件就能够减少我们枚举的个数
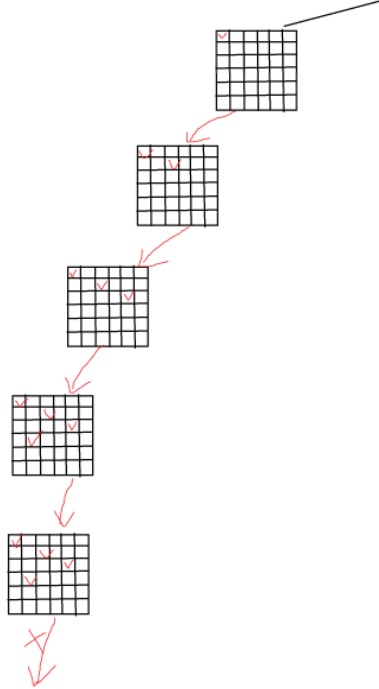
我们简单画一下决策树来:
这里并没有画完,大概理解一下,我们只要遍历填充即可
大概逻辑还是dfs将结果存放起来
我们发现,其实要知道对应的行列有没有放棋子很简单的,由于放了1行,那么只能从2行开始放置了。所以我们只要用循环一行一行的放即可,我们再创建一个bool col[N]数组去标记哪些列被标记了。如果对应的列被放了就跳过它。
那么对角线如何解决呢?
我们可以使用一次函数来解决它。以向下的行数为x轴,向右的列为y轴,每个对角线都有自己的一个表达式:
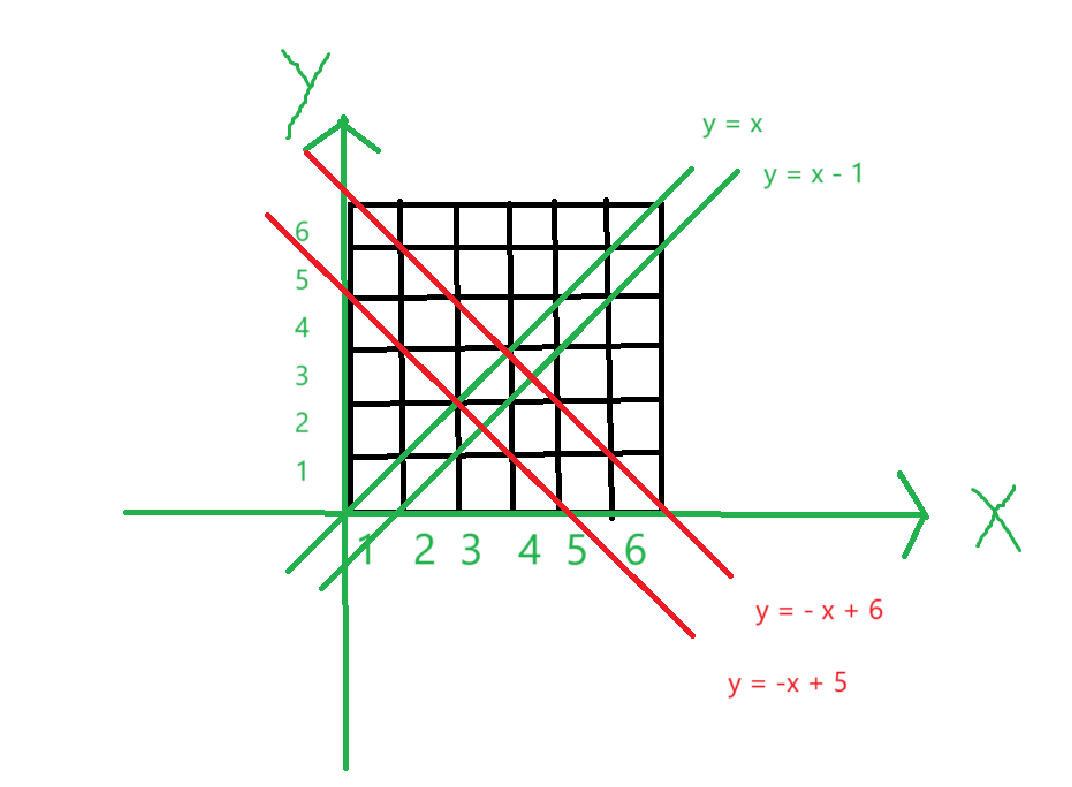
我们对于一个坐标位置就有两条对角线:y - x = n y + x = n
如果满足y - x = n或者y + x = n就代表对应的对角线已经有了棋子了!
我们只要将填过棋子的 y - x 和 y + x得到的值放在对应的数组就可以标记对角线了
但是有可能y - x会出现负数?怎么解决呢?
我们只要给y - x加上一个n值(偏移量)即可
现在bool st[2 * N];就可以标记对角线了,而且由于每个节点会出现两条对角线,所以要空间要开辟2 * N的大小!
我们需要统计前几个结果的路径所以还得用vector<int> path去标记成功的结果。
现在我们就来写一下代码吧:
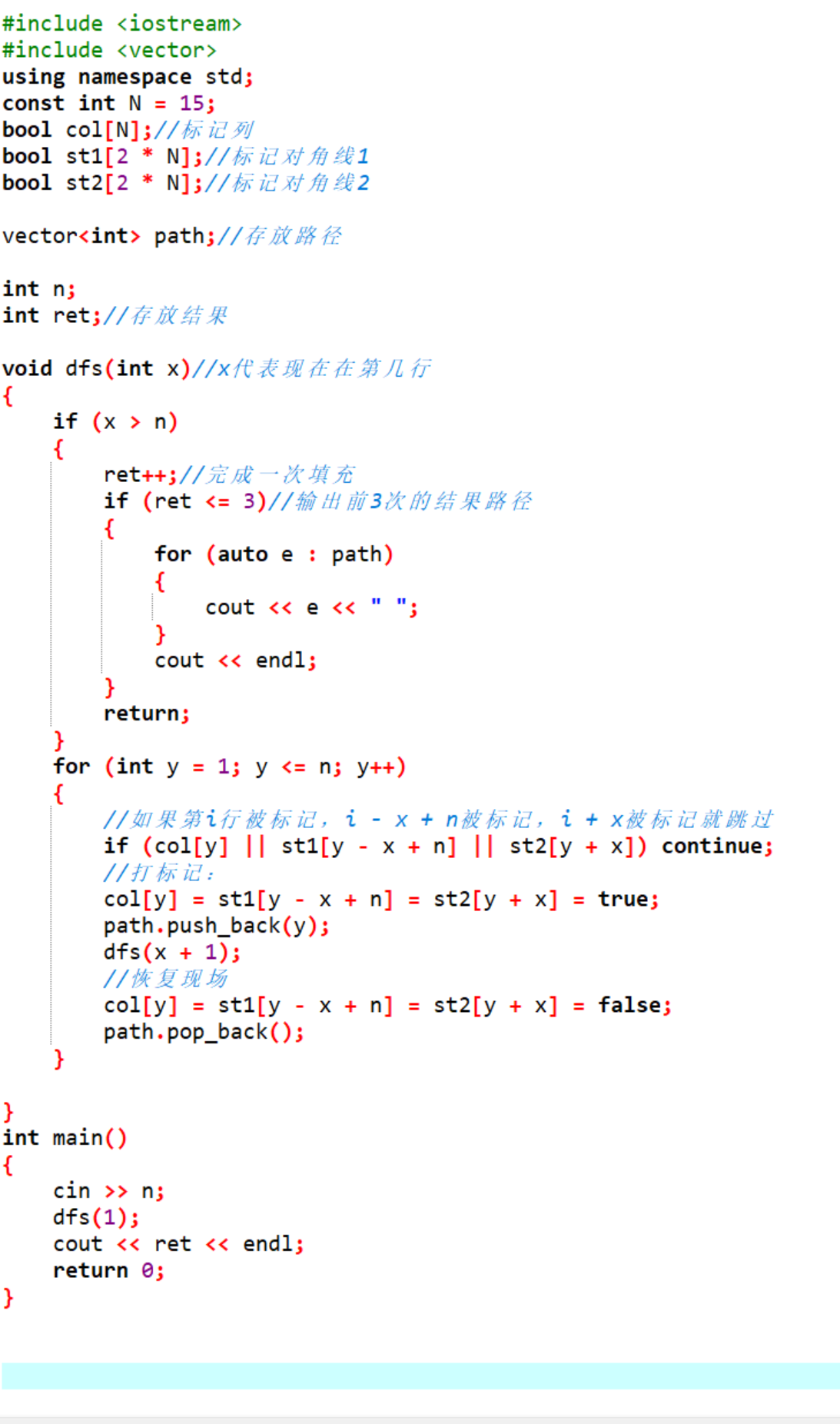
大家可以好好理解一下这段代码,再和博主我的思路画图结合一起来分析。
大家理解了其中的主要思维,就能够自己写出来了
5.数独
这道题题目讲的很简单给出一个未知的数独,然后让我们把它填完,再输出即可。
大家还是一样可以先自己思考一下该如何解决!
下面跟着博主的思路来看看这道题吧:
首先我们会接收到一个二维数组,这里面会有很多0,这些0就是我们需要去填充的部分。
对于每个0我们都可以在1---9的数字去填充
但是会因为其他已经有了数字的位置导致有些数不能填。
玩过数独的都知道,我们每行都是要在1-9去填充,3 * 3的格子内也得要在1--9
对于对应的行列,我们可以使用一个二维数组去标记第几行的哪几个数被填过,第几列的哪些数被填过。
bool row[N][N] ---------- row[i][x]表示第x行的i数被填充过
bool col[N][N] ---------- col[i][y]表示第y列的i数被填充过
那么对于这个3 * 3的格子怎么解决呢?
我们看看下面的图:
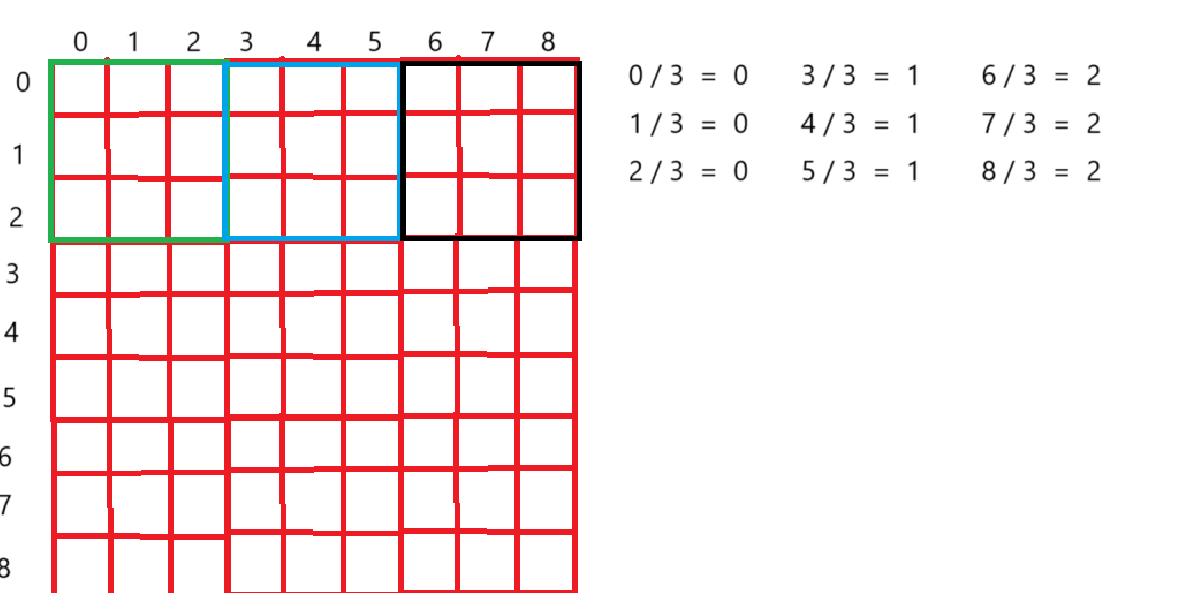
我们只要下标从 0 --- 8来标记数组,就可以通过对应的下标除以3就可以得到是第几个3 * 3的小格子
对应的这9 * 9的数独就有9个3 * 3的格子,就可以用对应点的x, y通过x / 3 , y / 3去找到对应的3 * 3格子
我们创建一个三维数组st来标记即可解决了
bool st[N][N][N] ----- st[x / 3][y / 3][i] ---- 就代表第x / 3,行y / 3列的3 * 3格子中填充了数i
现在我们最困难的地方已经解决,现在就是写代码的阶段,读者可以跟着思路自己去写一下!
代码如下:
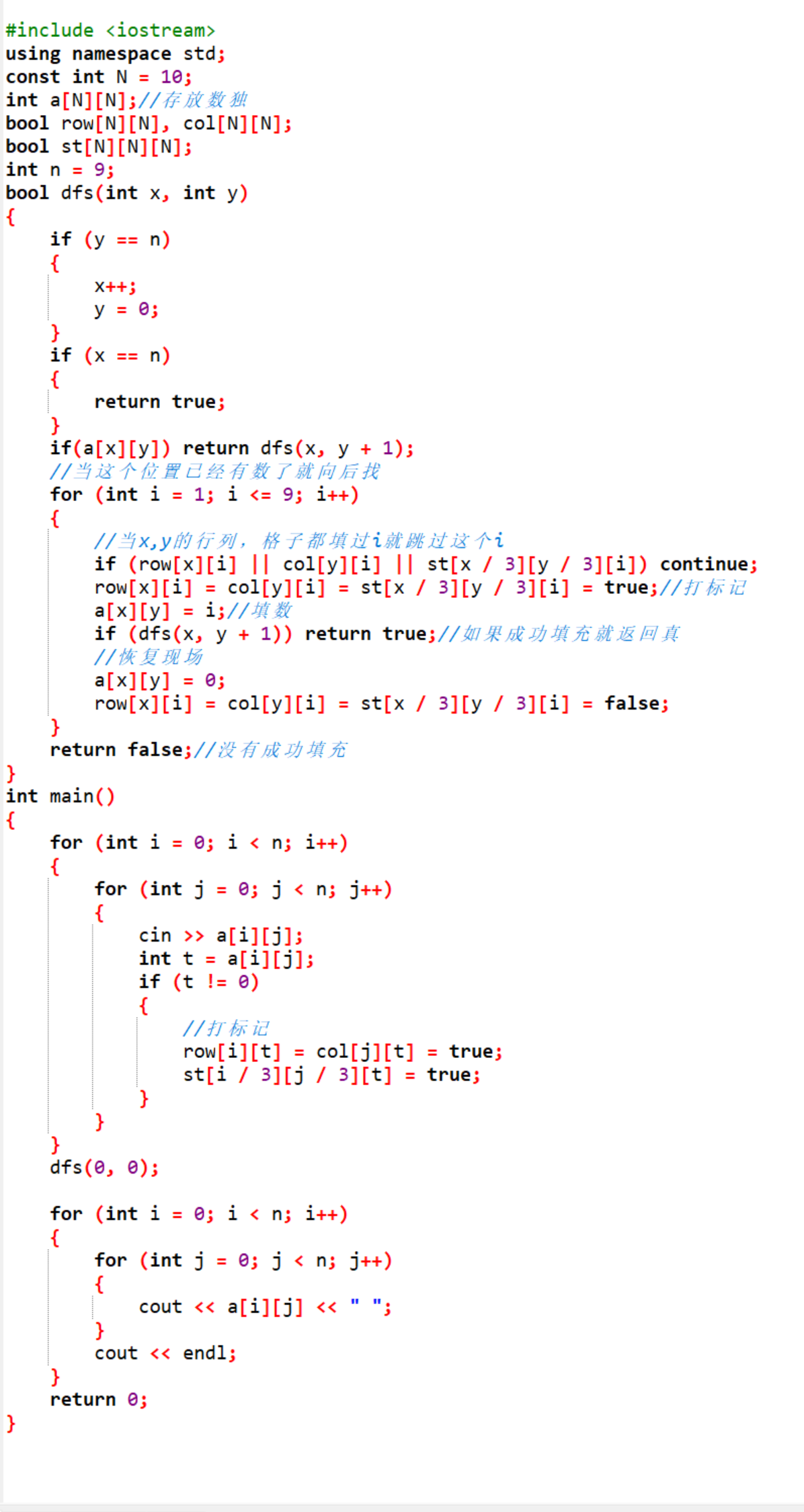
这道题中dfs里面还多出来了个判断y和x的合法性的判断,这个地方需要特别注意一下。
6.结语
很高兴大家能够看到这里,这一部分的题难度有所提高,大家要好好思考思考。
好好理解其中的思考过程,相信大家会有所收获的。
后面我会持续更新,大家多多点赞收藏+关注。






鼠标控制、可拓展陀螺仪与脚本控制)
)
)

)

)


)
——梯度处理、边缘检测、图像轮廓)

 用户管理命令)
