本文重点

全概率公式是概率论中的核心工具，用于计算复杂事件的概率。其核心思想是将复杂事件分解为若干互斥且穷尽的简单事件，通过计算各简单事件的概率及其条件概率，最终求得目标事件的概率。

全概率公式

全概率公式就是将复杂事件简单化，定义如下：

如果随机事件A1，A2，...,An是一个完备事件组，并且P(Ai)>0,i=1,2,...,n,还有一个随机事件B，那么：

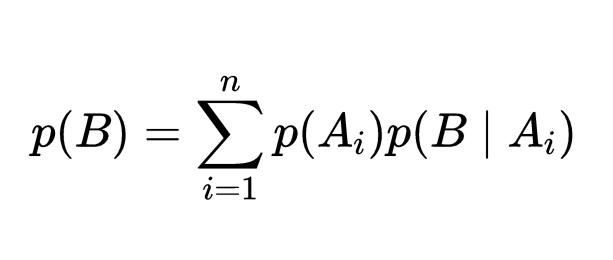
如公式所示，我们可以将随机事件B理解成一个复杂的事件，那么这个事件可以转变为右边的表现形式，右边的这种表现形式会非常简单，这就是全概率公式的厉害之处。

• B：目标事件，需计算其概率。
• P(Ai​)：先验概率，表示各原因发生的概率。
• P(B∣Ai​)：条件概率，表示在原因 Ai​ 下目标事件 B 发生的概率。

全概率公式的意义

全概率公式的意义在于，当直接计算P(