【1】引言
前序学习进程中,对软边界拉格朗日方程进行了初步构建。
其中约定了两个拉格朗日乘子要非负,其本质是要满足KKT条件。
今天就乘此次机会,在回顾一下KKT条件。
【2】定义
当问题无约束的时候,只要让函数梯度为零,就可以判定此处有极值点。当有约束存在时,梯度为零条件不再适用。
KKT条件适用的优化问题为:
目标函数最小化,minf(x)\min f(x)minf(x)
不等式约束:gi(x)≤0(i=1,2,...,m)g_{i}(x)\leq 0 (i=1,2,...,m)gi(x)≤0(i=1,2,...,m)
等式约束:$h_{j}(x)= 0 (j=1,2,…,p) $
其中,x∈Rnx\in R^nx∈Rn是自变量,f,gi,hjf,g_{i},h_{j}f,gi,hj均为连续可微函数。
如果x∗x*x∗是局部最优解,且满足约束规范,比如Slater条件,则存在拉格朗日乘子λi≥0,μ\lambda_{i}\geq 0,\muλi≥0,μ分别对应gi,hjg_{i},h_{j}gi,hj,使得以下条件同时成立。
首先是目标函数与约束函数的梯度通过乘子线性组合为零,也就是梯度平衡:
∇f(x∗)+∑i=1mλi∇gi(x∗)+∑j=1pμj∇hj(x∗)=0\nabla f(x^{*})+\sum_{i=1}^{m}\lambda_{i}\nabla g_{i}(x^{*})+\sum_{j=1}^{p}\mu_{j}\nabla h_{j}(x^{*})=0∇f(x∗)+i=1∑mλi∇gi(x∗)+j=1∑pμj∇hj(x∗)=0
需要说明的是,不等式约束乘子非负,且满足λi⋅gi(x∗)=0(i=1,2,...,m)\lambda_{i}\cdot g_{i}(x^{*})=0(i=1,2,...,m)λi⋅gi(x∗)=0(i=1,2,...,m)
上述公式在x∗x^*x∗是最优解时一定满足。
当gi(x∗)<0g_{i}(x^{*})<0gi(x∗)<0时,实际上就在不等式约束内部,相当于无用约束,此时λi=0\lambda_{i}=0λi=0,所以λi⋅gi(x∗)=0\lambda_{i} \cdot g_{i}(x^{*})=0λi⋅gi(x∗)=0;
当gi(x∗)=0g_{i}(x^{*})=0gi(x∗)=0时,此时来到了不等式约束边缘,为了实现取极值,一定会满足梯度平衡,可参考拉格朗日乘数法加深理解,此时必有:∇f(x∗)+∑i=1mλi∇gi(x∗)=0\nabla f(x^{*})+\sum_{i=1}^{m}\lambda_{i}\nabla g_{i}(x^{*})=0∇f(x∗)+i=1∑mλi∇gi(x∗)=0因为gi(x∗)=0g_{i}(x^{*})=0gi(x∗)=0所以λi⋅gi(x∗)=0\lambda_{i}\cdot g_{i}(x^{*})=0λi⋅gi(x∗)=0。
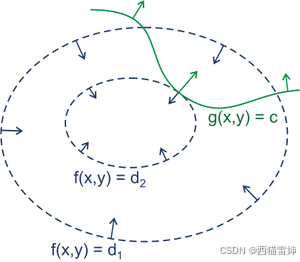
下图可做辅助理解。
【3】总结
回顾了KKT条件的基本定义内容。







)

)









