在深度学习框架普及的今天，回归基础用NumPy从头实现机器学习模型具有特殊意义。本文将完整演示如何用纯NumPy实现二次函数回归任务，揭示机器学习底层原理。整个过程不使用任何深度学习框架，每一行代码都透明可见。

---

1. 环境配置与数据生成

import numpy as np
from matplotlib import pyplot as plt 设置随机种子保证可复现性 
np.random.seed(100)  生成训练数据：100个点在[-1,1]区间均匀分布 
x = np.linspace(-1, 1, 100).reshape(100, 1)基于y=3x²+2生成目标值，并添加高斯噪声
y = 3 * np.power(x, 2) + 2 + 0.2 * np.random.rand(x.size).reshape(100, 1)

**数据可视化结果： **

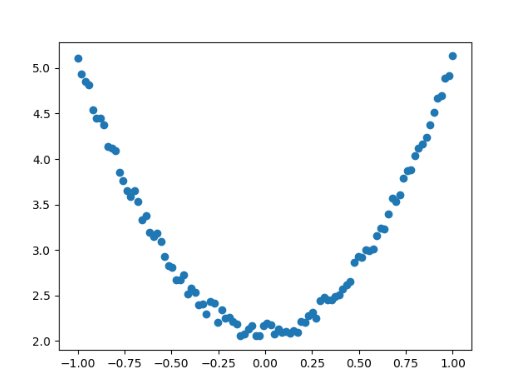
散点图展示了添加噪声后的数据分布，我们的目标是找到最佳拟合曲线$y=w{x}^2+b$

---

2. 模型初始化与核心参数

随机初始化待学习参数
w = np.random.rand(1, 1)  # 权重参数 (理论值应接近3)
b = np.random.rand(1, 1)  # 偏置项 (理论值应接近2)lr = 0.001  # 学习率 (梯度下降步长)
epochs = 800  # 训练轮数

初始参数可视化：

print(f"初始参数: w={w[0][0]:.4f}, b={b[0][0]:.4f}")
典型输出: w=0.7123, b=0.1582 (每次运行结果不同)

---

3. 训练过程与数学原理

3.1 前向传播计算预测值

y_pred = np.power(x, 2) * w + b

3.2 损失函数定义

采用均方误差(MSE)的变体：

loss = 0.5 * (y_pred - y)  2 
total_loss = loss.sum()  # 所有样本损失之和 

3.3 梯度计算解析

关键数学推导（链式法则）：

权重w的梯度: ∂Loss/∂w = Σ(y_pred - y)*x² 
grad_w = np.sum((y_pred - y) * np.power(x, 2))偏置b的梯度: ∂Loss/∂b = Σ(y_pred - y)
grad_b = np.sum((y_pred - y))

3.4 参数更新（梯度下降）

w -= lr * grad_w  # w = w - η·(∂Loss/∂w)
b -= lr * grad_b  # b = b - η·(∂Loss/∂b)

---

4. 完整训练代码

for epoch in range(epochs):# 前向传播y_pred = np.power(x, 2) * w + b # 损失计算 loss = 0.5 * (y_pred - y)  2total_loss = loss.sum()# 梯度计算grad_w = np.sum((y_pred - y) * np.power(x, 2))grad_b = np.sum((y_pred - y))# 参数更新w -= lr * grad_w b -= lr * grad_b# 每100轮打印训练进展 if epoch % 100 == 0:print(f"Epoch {epoch}: w={w[0][0]:.4f}, b={b[0][0]:.4f}, Loss={total_loss:.4f}")

训练过程输出：

Epoch 0: w=0.9461, b=0.3827, Loss=160.9256 
Epoch 100: w=2.1433, b=1.8047, Loss=1.8925 
Epoch 200: w=2.6555, b=2.0404, Loss=0.4583
Epoch 300: w=2.8543, b=2.1023, Loss=0.2985 
...
Epoch 700: w=2.9887, b=2.0161, Loss=0.2502 

---

5. 训练结果可视化

生成预测曲线 
x_test = np.linspace(-1, 1, 30).reshape(30, 1)
y_test = np.power(x_test, 2) * w + b 绘制结果对比图 
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', alpha=0.5, label='真实数据')
plt.plot(x_test, y_test, 'r-', linewidth=3, label='模型预测')
plt.plot(x_test, 3*x_test2+2, 'g--', label='理论曲线')
plt.xlim(-1, 1)
plt.ylim(2, 6)
plt.legend()
plt.title('NumPy实现回归结果')
plt.show()输出最终参数
print(f"训练结果: w={w[0][0]:.4f} (接近理论值3), b={b[0][0]:.4f} (接近理论值2)")

可视化结果：

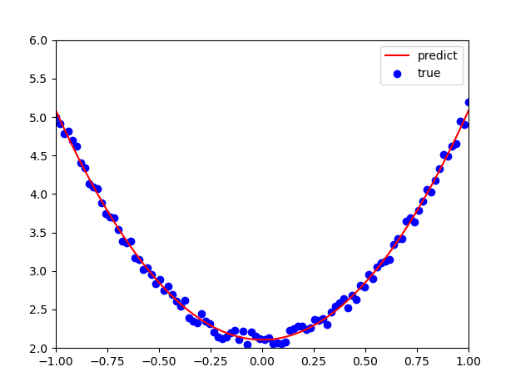
红色实线为模型预测曲线，绿色虚线为理论曲线$y=3x^2+2$，蓝色点为带噪声的训练数据

---

6. 关键技术解析

1. 梯度下降的本质

通过参数空间中的"下坡运动"寻找最优解，学习率控制步长大小：

• 学习率过大 → 震荡发散
• 学习率过小 → 收敛缓慢
• 本例0.001是多次试验后的平衡值

2. 手动求导的意义

# 关键导数计算
grad_w = np.sum((y_pred - y) * np.power(x, 2))

理解此式需掌握：

• 链式法则：∂Loss/∂w = (∂Loss/∂y_pred)·(∂y_pred/∂w)
• 损失函数导数：∂Loss/∂y_pred = (y_pred - y)
• 模型输出导数：∂y_pred/∂w = x²

3. 批量梯度下降特点

• 每次迭代使用全部样本（不同于随机梯度下降）
• 计算稳定但内存消耗大
• 适合中小规模数据集

---

7. 拓展思考

1. 学习率动态调整

# 添加学习率衰减 
if epoch % 200 == 0:lr *= 0.8  # 每200轮衰减20%

2. 添加正则化项（L2正则化）

# 修改损失函数
lambda_reg = 0.01  # 正则化系数 
loss = 0.5*(y_pred-y)2 + 0.5*lambda_reg*(w2)

3. 动量优化（Momentum）

# 添加动量项
beta = 0.9  # 动量系数 
v_w = beta*v_w + (1-beta)*grad_w 
w -= lr * v_w

---

8. 总结与启示

NumPy实现的价值：

• 透明机制：每个运算步骤完全可见
• ⚙️ 数学本质：揭示梯度下降和反向传播核心原理
• 🔍 调试优势：便于定位问题和理解优化过程

局限性：

• 📈 仅适合简单模型
• ⏱️ 复杂网络需大量重复代码
• 缺乏自动微分等高级功能

通过这个基础实现，我们能更深刻地理解PyTorch/TensorFlow等框架封装的高级功能背后的数学原理，为后续学习打下坚实基础。