一、作品详细简介

1.1附件文件夹程序代码截图

 全部完整源代码，请在个人首页置顶文章查看：

学行库小秘_CSDN博客https://blog.csdn.net/weixin_47760707?spm=1000.2115.3001.5343

1.2各文件夹说明

1.2.1 main.m主函数文件

该MATLAB代码实现了一个基于K近邻（KNN）算法的回归预测模型，主要步骤及详细解释如下：

1. 数据导入与预处理

res = xlsread('数据集.xlsx');

• 功能：从Excel文件数据集.xlsx中读取数据，存储到矩阵res中。
• 注意：数据集应包含103行样本，前7列为特征，第8列为目标变量。

2. 划分训练集与测试集

• 步骤：
  1. randperm(103) 生成1~103的随机排列，实现数据随机打乱。
  2. 前80个样本（80%）作为训练集，后23个样本（23%）作为测试集。
  3. P_train/P_test：训练/测试特征（7维），转置为 7×M 和 7×N 矩阵。
  4. T_train/T_test：训练/测试目标值，转置为行向量。
  5. M和N记录训练/测试样本数量。

3. 数据归一化

• 目的：消除量纲影响，提升模型收敛速度。
• 操作：
  • 特征归一化：对训练集P_train归一化到[-1, 1]，保存参数ps_input；测试集用相同参数归一化。
  • 目标值归一化：对T_train归一化，保存参数ps_output；测试目标值同理。

4. 数据转置

• 原因：MATLAB的KNN建模函数fitcknn要求输入格式为 样本×特征（行样本）。
• 结果：p_train变为 80×7，t_train变为 80×1（测试集同理）。

5. 构建KNN模型

• 参数：
  • NumNeighbors=2：使用最近的2个邻居进行预测。
  • Distance='euclidean'：采用欧氏距离计算样本相似度。
• 输出：训练好的KNN模型knn。

6. 模型预测

• 结果：t_sim1和t_sim2为归一化后的预测值。

7. 反归一化

• 功能：将预测值转换回原始量纲，便于结果对比。

8. 评估指标计算

(1) 均方根误差 (RMSE)

• 意义：衡量预测值与真实值的偏差，值越小越好。

(2) 决定系数 (R²)

• 意义：模型解释方差的比例，越接近1说明拟合越好。

(3) 平均绝对误差 (MAE)

• 意义：预测误差绝对值的平均值，鲁棒性强于RMSE。

(4) 平均偏差误差 (MBE)

• 意义：预测误差的平均值，反映系统偏差（正偏高/负偏低）。

9. 结果可视化

关键注意事项

1. KNN用于回归问题：
   虽然fitcknn是分类函数，但目标变量T_train为连续值时，MATLAB会自动执行回归（预测结果为最近邻的平均值）。
2. 维度一致性：
   多次转置操作（'）确保训练/预测时维度匹配（如T_train'与T_sim1对齐）。
3. 归一化重要性：
   所有特征和目标值必须归一化，避免数值差异导致的距离计算偏差。
4. 随机性：
   randperm使每次运行的数据划分不同，建议固定随机种子（如rng(0)）以复现结果。

代码改进建议

1. 回归专用函数：
   严格回归问题建议使用fitrknn（需MATLAB版本支持）：

1. 交叉验证：
   使用crossval评估模型稳定性，避免过拟合：

1. K值优化：
   通过循环测试不同K值，选择最优参数：

此代码完整实现了KNN回归预测流程，适用于连续目标值的预测任务（如房价预测、销量预估等）。

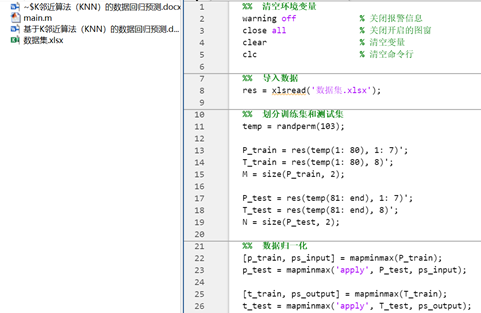
图2  main.m主函数文件部分代码

1.2.2 数据集文件

数据集为Excel数据csv格式文件，可以方便地直接替换为自己的数据运行程序。原始数据文件包含7列特征列数据和1列输出标签列数据，一共包含103条样本数据，具体如图所示。

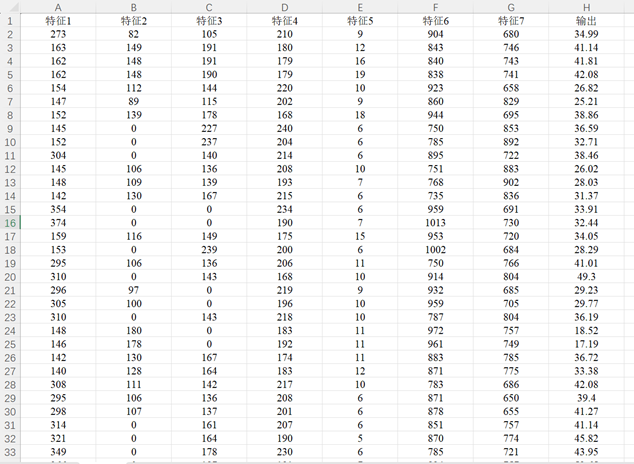
二、代码运行结果展示

本代码实现了一个基于K近邻（KNN）算法的回归预测模型，其核心功能是：从数据集中随机划分训练集和测试集，通过数据归一化预处理后，使用K=2的KNN模型进行训练和预测，最后通过反归一化得到原始量纲的预测结果，并计算多种评估指标（RMSE、R²、MAE、MBE）以及可视化展示预测值与真实值的对比效果，从而完成对连续目标变量的建模和性能评估。

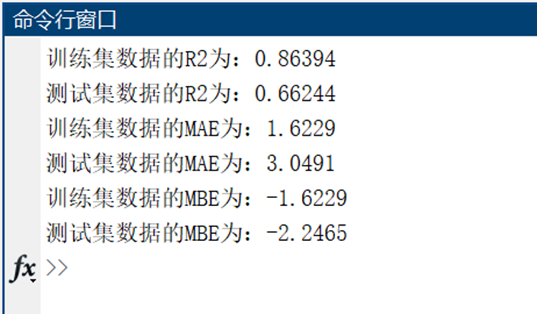
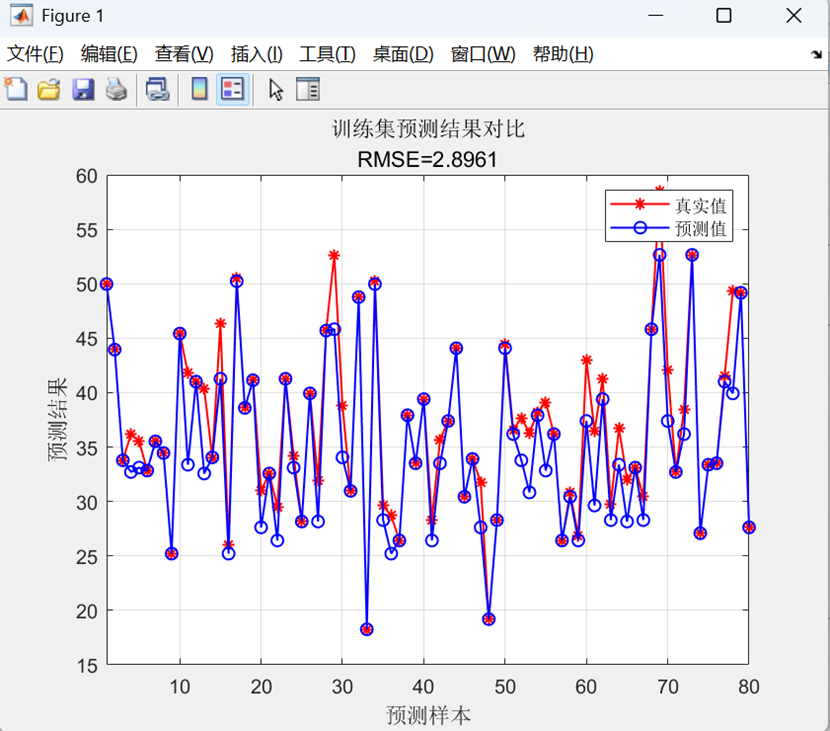
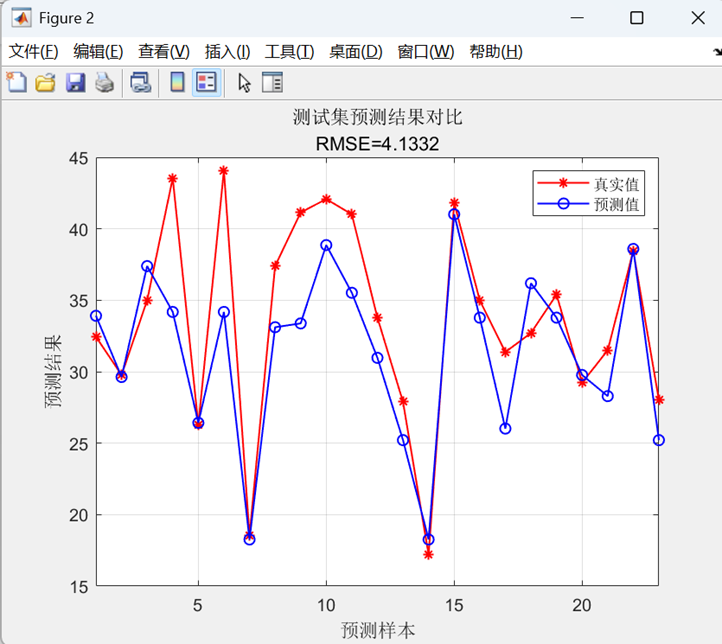
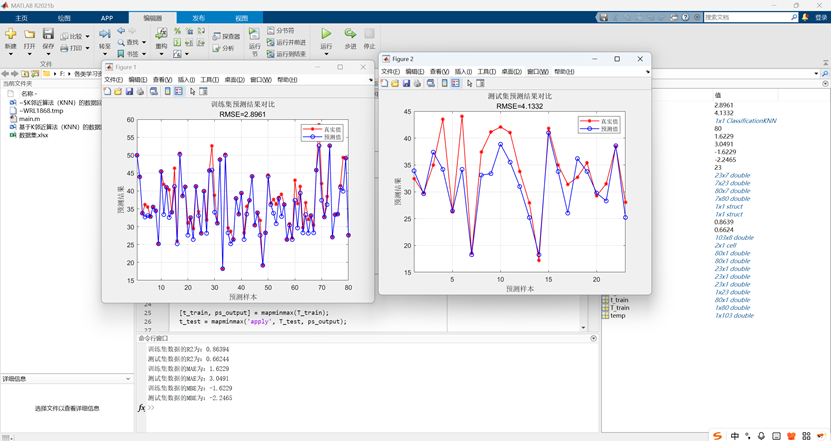
三、注意事项:

1.程序运行软件推荐Matlab 2018B版本及以上；

2.所有程序都经过验证，保证程序可以运行。此外程序包含简要注释，便于理解。

3.如果不会运行，可以帮忙远程运行原始程序以及讲解和其它售后，该服务需另行付费。

4. 代码包含详细的文件说明，以及对每个程序文件的功能注释，说明详细清楚。

5.Excel数据，可直接修改数据，替换数据后直接运行即可。