核心3D数据结构

1.1 PointCloud（点云）

• 原理：点云是最基础、最直接的 3D 数据表示形式，直接来源于大多数 3D 传感器。它记录了物体表面一系列采样点的三维坐标 (x, y, z)，并可扩展存储每个点的颜色 (r, g, b)、法线 (nx, ny, nz)、强度等属性。
  

import open3d as o3d
import numpy as np# 创建一个简单的点云
points = np.random.rand(1000, 3)  # 1000个随机点
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)# 估计法线（关键算法）
# 使用 K近邻 策略，为点云 pcd 中的每一个点，计算其最近 30 个点，并基于这些点来估计该点的法向量。
pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamKNN(knn=30)) # 可视化
o3d.visualization.draw_geometries([pcd], point_show_normal=True)

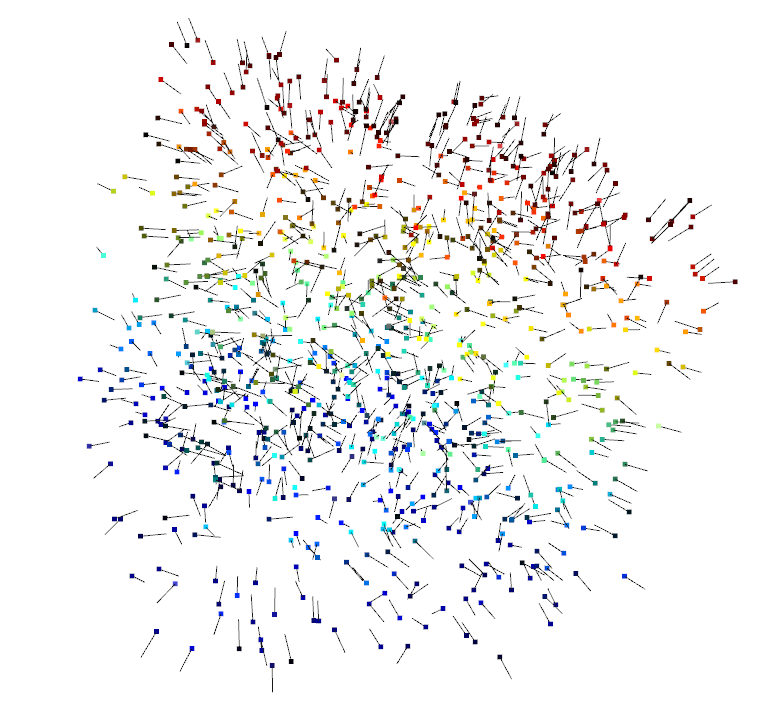
最近邻搜索 (KNN/Radius) 与空间索引（KDTree/Octree）

法线估计 (Normal Estimation)

原理
基于主成分分析 (PCA)。核心思想：一个点及其邻域点可以拟合出一个局部微平面。这个平面的法线方向就是该点的法线方向。

1. 邻域查询：对于点 $p_i$，利用 KDTree 找到其 K 个最近邻点 $N(i)=p_{i1},p_{i2},...,p_{ik}$。
2. 计算质心：计算邻域点的质心（中心点）： $\bar{p}=\frac{1}{k}{\sum }_{j=1}^k{p}_{ij}$
3. 构建协方差矩阵：计算协方差矩阵 $C$，它描述了邻域点围绕质心的分布情况： $C=\frac{1}{k}{\sum }_{j=1}^k(p_{ij}-\bar{p})\cdot (p_{ij}-\bar{p}{)}^T$
4. PCA 分解：对协方差矩阵 $C$ 进行特征值分解，得到特征值 ${\lambda }_1,{\lambda }_2,{\lambda }_3$(${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\ge 0$) 和对应的特征向量$\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3}$。
5. 法线确定：最小特征值 ${\lambda }_3$ 对应的特征向量 $\overrightarrow{v_3}$即为法线方向。因为数据在法线方向上的变化最小（方差最小），而在切平面上变化最大。
   

import open3d as o3d
import numpy as np# 生成示例点云（一个平面加上一些噪声，法线应大致指向z轴正方向）
mesh = o3d.geometry.TriangleMesh.create_box(width=2.0, height=1.0, depth=0.2)
mesh.translate((-1.0, -0.5, -0.1)) # 平移使原点在中心
pcd = mesh.sample_points_poisson_disk(500) # 从网格采样生成点云# 估计法线
# 使用KNN策略，k=30
pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamKNN(knn=30))# 为了可视化效果，统一法线方向（使其指向[0,0,1]大致方向）
pcd.orient_normals_to_align_with_direction(orientation_reference=np.array([0., 0., 1.]))# 可视化：按法线方向着色
# 将法向量（[-1,1]）映射到RGB颜色（[0,1]）进行可视化
pcd.paint_uniform_color([0.5, 0.5, 0.5]) # 先设置一个基础灰色
o3d.visualization.draw_geometries([pcd],point_show_normal=True,window_name="Point Cloud with Normals")# 访问估计的法线
normals = np.asarray(pcd.normals)
print(f"First 5 normals:\n{normals[:5]}")

聚类分割 (基于欧氏距离的聚类)

import open3d as o3d
import numpy as np# 创建包含两个明显分开的簇的点云
points1 = np.random.rand(100, 3) * 0.5 + np.array([0, 0, 0])  # 簇1，围绕(0,0,0)
points2 = np.random.rand(100, 3) * 0.5 + np.array([2, 2, 2])  # 簇2，围绕(2,2,2)
points = np.vstack((points1, points2))pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)# 可视化原始点云
o3d.visualization.draw_geometries([pcd], window_name="Original Point Cloud")# 使用Open3D进行基于欧氏距离的聚类
# 参数1: eps - 邻域搜索半径
# 参数2: min_points - 形成一个簇所需的最少点数
labels = np.array(pcd.cluster_dbscan(eps