目录

 

力扣.1054距离相等的条形码

力扣767.重构字符串

力扣47.全排列II

力扣980.不同路径III

力扣509.斐波那契数列（记忆化搜索)

---

力扣.1054距离相等的条形码

是否策略正确

但是假如 1 2 2 此时 1_2     此时中间只能填写2，但是就不对了，所以，限定条件，先处理出现次数最多的次数，其余无所谓 

2_2

证明:题目一定有解，性质:两个两个一组

（n+1）/2组，出现次数最多的次数，一定是小于(n+1)/2个，那么

假如出现次数最多的，等于(n+1)/2,一定正确

第二个，最多的，小于(n+1)/2, 假如你   前面        o _ o_ o_ o_ x_ x_x 假如你第二个没填写完，就还是x,但是你不可能说是x填重复的，换句话，x绝对不可能绕过一圈来再次相邻，

class Solution {public int[] rearrangeBarcodes(int[] barcodes) {Arrays.sort(barcodes);int n=barcodes.length;Map<Integer,Integer>map=new HashMap<>();int[]a=new int[n];int max=0;int maxcount=0;
//第一个点，该定义变量就去定义，不要老想着优化for(int i=0;i<n;i++){map.put(barcodes[i],map.getOrDefault(barcodes[i],0)+1);if(maxcount<map.get(barcodes[i])){max=barcodes[i];maxcount=map.get(barcodes[i]);}}//先处理出现次数最多的那个数字int index=0;//统计处那个字符数字最多，然后给他填上
//最难的一步就是maxcount你是否能理清楚for(int i=0;i<maxcount;i++){a[index]=max;index+=2;}//处理剩下的数，可以直接删除，也可以遍历时候跳过，不要太纠结map.remove(max);for(int x:map.keySet()){for(int i=0;i<map.get(x);i++){if(index>=n) index=1;a[index]=x;index+=2;}}return a;}
}

力扣767.重构字符串

跟上面那个题思路一样，只需要进行一个判断，是否满足条件就行。

max>(n+1)/2的情况下，就返回空字符串

class Solution {public String reorganizeString(String s) {HashMap<Character,Integer>map=new HashMap<>();//(n+1)/2char[]a=s.toCharArray();int n=a.length;char max=a[0];int maxCount=0;for(int i=0;i<n;i++){map.put(a[i],map.getOrDefault(a[i],0)+1);if(maxCount<map.get(a[i])){max=a[i];maxCount=map.get(a[i]);}}if(maxCount>(n+1)/2)return "";else{StringBuffer sb=new StringBuffer();int index=0;for(int i=0;i<maxCount;i++){a[index]=max;index+=2;}map.remove(max);for(char x:map.keySet()){for(int i=0;i<map.get(x);i++){if(index>=n)index=1;a[index]=x;index+=2;}}return sb.append(a).toString();}}
}

力扣47.全排列II

1.同一个节点都所有分支中，相同的元素只可以选择一次

同一个数只能使用一次

并且我们需要对数组，进行一个排序，去确定 check[i]==true||nums[i]与nums[i-1]是否相同

同一层的话，不用考虑 check[i-1]==false

考虑不合法的分支(这里的i不可以等于0,0一定合法，不用判断) 

check[i]==true ||(i!=0&&nums[i]==nums[i-1]&&check[i-1]==false)

假如i位置是true代表当前位置已经被使用了，或者，当前位置的前一个没有被使用，但是我和你是在一层，换句话说，我们属于一层，那么就应该剪枝

考虑合法的分支(这里面的i是可以等于0的(

check[i]=false&&(nums[i]!=nums[i-1]||check[i-1]==true(此时的条件是a[i]=a[i-1])      )

class Solution {List<List<Integer>>ret=new ArrayList<>();List<Integer>ans=new ArrayList<>();boolean[]check;int n;//伴随着就是如何剪枝public void dfs(int pos,int []nums){if(pos==n){ ret.add(new ArrayList<>(ans)); return ;}for(int i=0;i<n;i++){if((check[i]==true)||(i!=0&&check[i-1]==false&&nums[i]==nums[i-1])){continue;}    check[i]=true;ans.add(nums[i]);   dfs(pos+1,nums);ans.remove(ans.size()-1);check[i]=false;;}}public List<List<Integer>> permuteUnique(int[] nums) {n=nums.length;Arrays.sort(nums);check=new boolean[n];dfs(0,nums);    return ret;}
}

力扣980.不同路径III

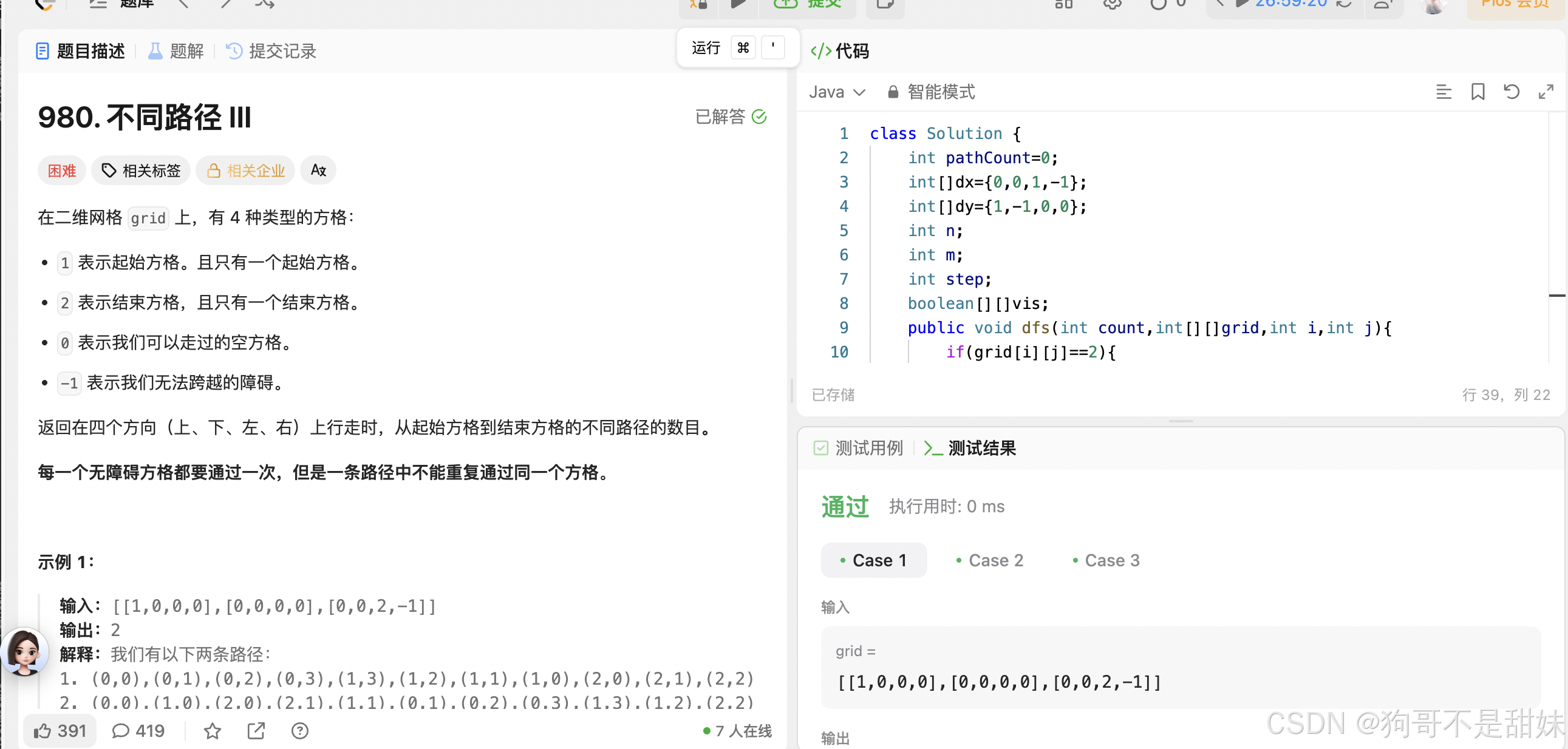
step++,然后到达终点之后，路径++，然后不断递增就好

这个要注意，最后才调用这个函数要让step走完

class Solution {int pathCount=0;int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};int n;int m;int step;boolean[][]vis;public void dfs(int count,int[][]grid,int i,int j){if(grid[i][j]==2){if(count==step)pathCount++;return;}for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0&&x<n&&y>=0&&y<m&&vis[x][y]==false&&(grid[x][y]==0||grid[x][y]==2)){vis[x][y]=true;dfs(count+1,grid,x,y);vis[x][y]=false;}}  }public int uniquePathsIII(int[][] grid) {n=grid.length;m=grid[0].length;vis=new boolean[n][m];int bx=0;int by=0;//这么判断是否走完全了for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==1){bx=i;by=j;vis[bx][by]=true;}else if(grid[i][j]==0||grid[i][j]==2)step++;}}dfs(0,grid,bx,by);return pathCount;}
}

力扣509.斐波那契数列（记忆化搜索)

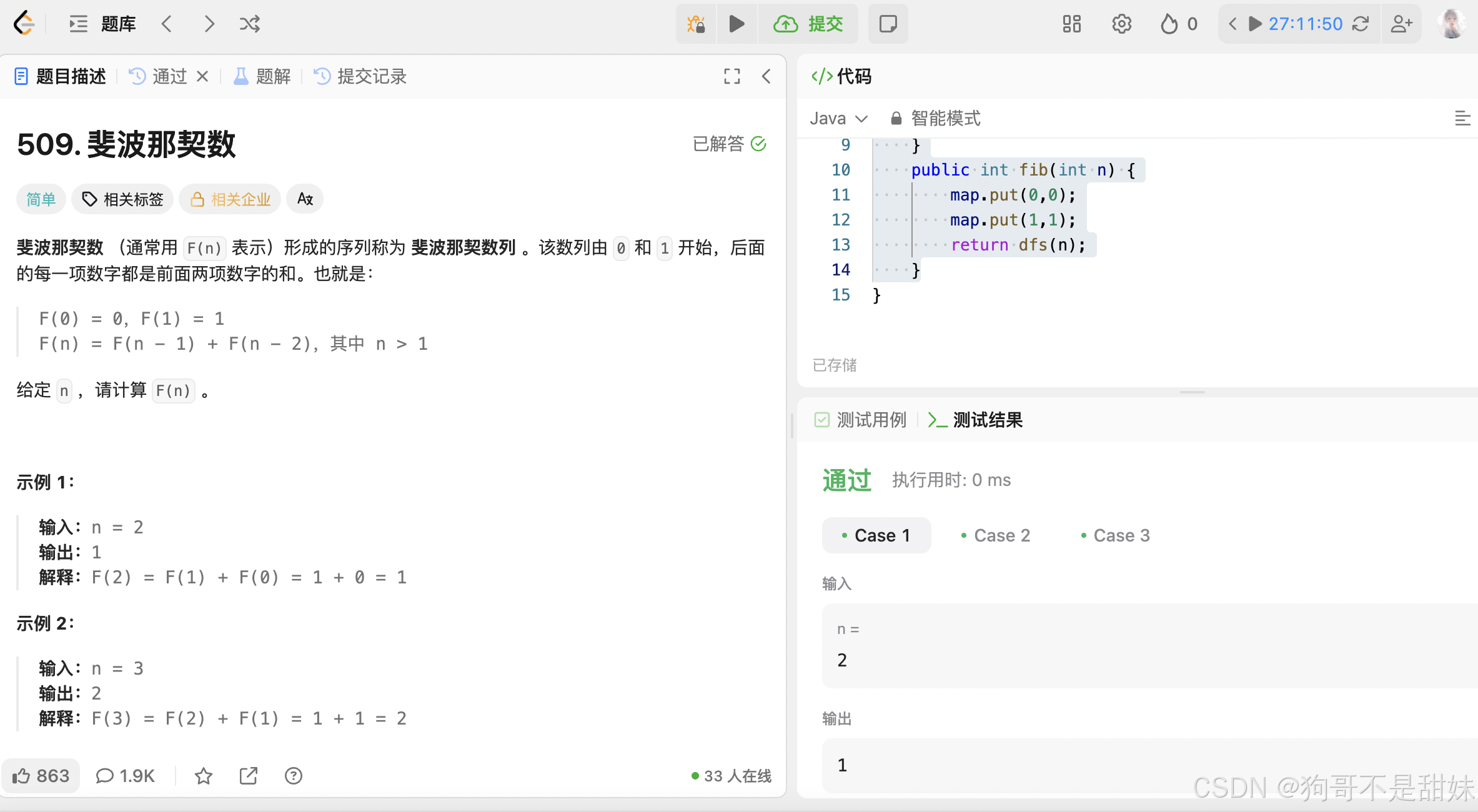
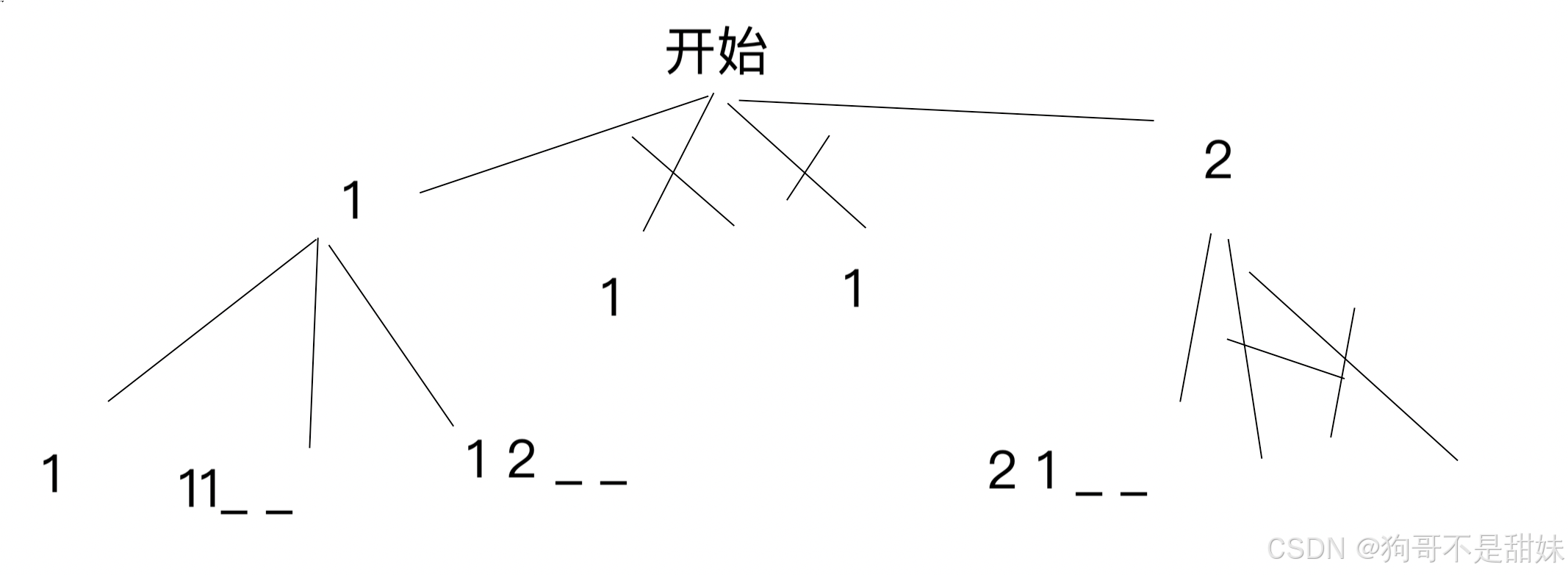
存储在map，假如有值，直接返回，就不用再去递归了。

class Solution {Map<Integer,Integer>map=new HashMap<>();public int dfs(int n){if(map.containsKey(n)){return map.get(n);}   map.put(n,dfs(n-1)+dfs(n-2));return map.get(n);}public int fib(int n) {map.put(0,0);map.put(1,1);return dfs(n);}
}