锋哥原创的Scikit-learn Python机器学习视频教程：

2026版 Scikit-learn Python机器学习 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili

课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识，包括机器学习概述，特征工程(数据集，特征抽取，特征预处理，特征降维等)，分类算法(K-临近算法，朴素贝叶斯算法，决策树等)，回归与聚类算法(线性回归，欠拟合，逻辑回归与二分类，K-means算法)等。

Scikit-learn Python机器学习 - 特征降维 压缩数据 - 特征提取 - 主成分分析 (PCA)

PCA通过线性变换将原始特征转换为一组线性不相关的变量（主成分），按方差大小排序。

PCA的核心思想是：将原始高维特征通过线性变换映射到新的低维坐标系中，这个新坐标系的坐标轴（主成分）按照能够保留原始数据最大方差的方向依次排列。

这意味着第一个新坐标轴（第一主成分）保留了数据中最大程度的方差，第二个新坐标轴（第二主成分）在与第一个正交的前提下保留次大方差，以此类推。

🧠 直观理解：一个经典的比喻

想象你在黑暗中从不同角度观察一个三维物体（比如一个倾斜的椭圆盘子），并记录下它在二维平面上的影子。

• 某些角度下的影子（比如正上方）可能看起来只是一个短线，丢失了大量关于盘子形状的信息。

• 某些角度下的影子（比如从盘子侧面）则能最大程度地展现它的形状和大小（一个椭圆）。

PCA要做的就是自动找到那个“最佳观测角度”，使得投影后的影子（低维数据）能包含原始物体（高维数据）最多的信息。而这个“信息量”，在PCA中就用方差来衡量。方差越大，意味着数据点在新坐标轴上分布得越分散，保留的信息就越多。

📊 数学原理与计算步骤（可分步理解）

假设有一个包含 m 个样本和 n 个特征的数据集 X )，其中 X = [x_1, x_2, …, x_m] ，每个样本 x_i 是一个 n 维向量。

（ 快速理解这个PCA算法原理，可以查看 视频 主成分分析 (PCA) 转载自 抖音 动画讲编程 ）

⚙️ 关键参数与概念（以Scikit-learn为例）

参数/概念	说明
n_components	最重要的参数。指定要保留的主成分个数 k。可以设为整数（如 2），也可以设为 0 到 1 之间的浮点数（如 0.95，表示保留95%的原始方差）。
svd_solver	指定求解器。通常使用默认的 'auto' 即可。对于大型数据，使用 'randomized' 的随机SVD方法会更高效。
explained_variance_	属性。一个数组，表示每个主成分所捕获的方差大小（即特征值）。
explained_variance_ratio_	属性。一个数组，表示每个主成分所捕获的方差占总方差的百分比。这是决定 k 取多少的关键依据。
components_	属性。投影矩阵 $W$，每一行是一个主成分（特征向量）。

我们来看一个示例：

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris# 加载数据
iris = load_iris()
X, y = iris.data, iris.target# 1. 标准化数据（至关重要！）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 2. 初始化PCA，保留2个主成分用于可视化
pca = PCA(n_components=2)# 3. 训练转换数据
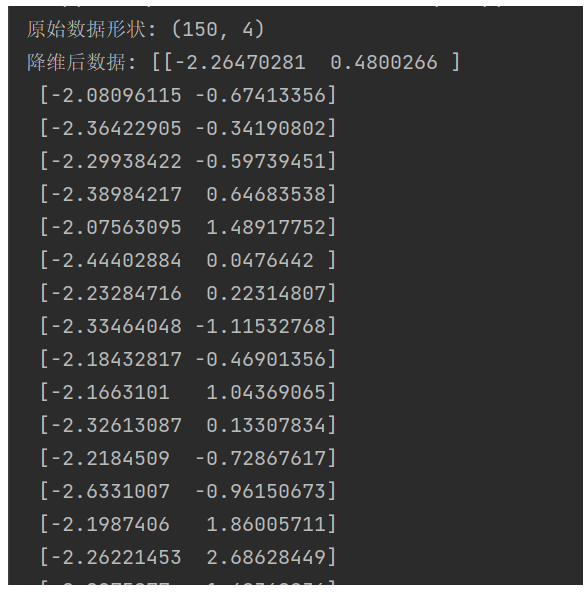
X_pca = pca.fit_transform(X_scaled)print("原始数据形状:", X.shape)
print("降维后数据:", X_pca)

运行结果：