决策树是一种基于特征分割的监督学习算法，通过递归分割数据空间来构建预测模型。

1.1、决策树模型基本原理

决策树思想的来源朴素，程序设计中的条件分支结构就是 if-then结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法。为了更好理解决策树具体怎么分类的，我们通过以下问题例子?

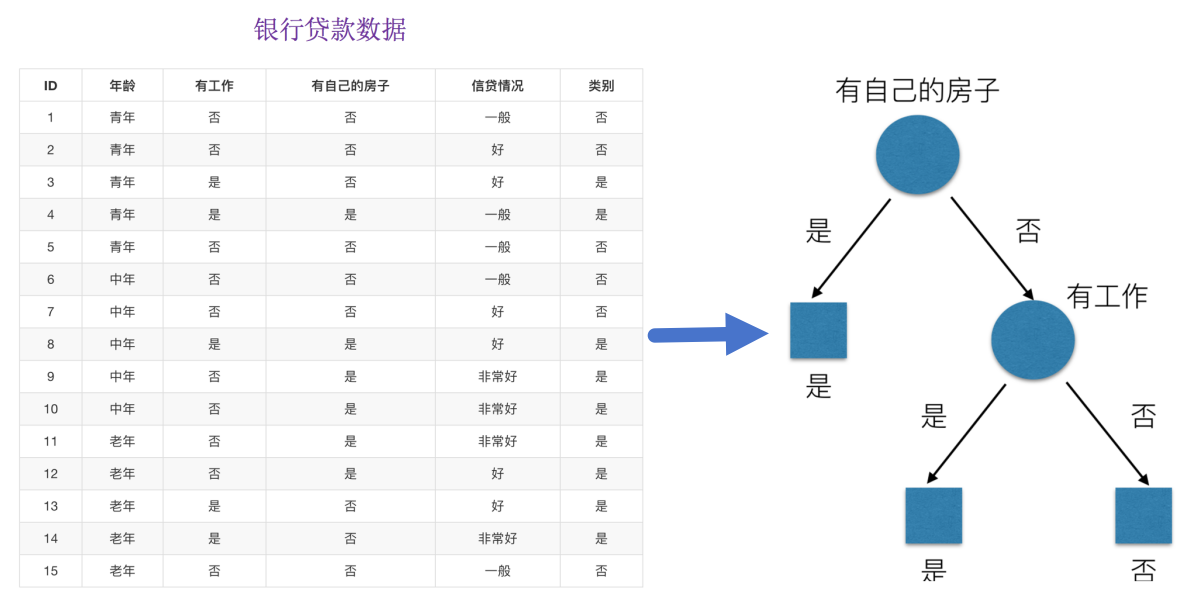
问题：如何对这些客户进行分类预测？你是如何去划分？我们怎么知道这些特征哪个更好放在最上面，那么决策树的真是划分是这样的。

1.2、决策树模型的建树依据

为了易于生成决策树的理解，下面我们使用“信息熵”来说明决策树的构建。

1.2.1、信息熵

       需要用到信息论专业的知识！此处，通过经典“猜冠军”的例子来引入信息熵：

       我们玩个猜测类游戏，猜猜下图32支球队那支是冠军。并且猜测错误会付出代价，每猜错一次给一块钱，告诉我是否猜对了，那么我需要掏多少钱才能知道谁是冠军呢？ （这有个前提是：你不知道任意球队的信息、历史比赛记录、球队实力等）。

为了使代价最小，可以使用二分法来猜测：我可以把球依次编上号，从1到32，然后提问：冠 军在1-16号吗？依次询问，只需要五次，就可以知道结果。

 我们来看这个式子：

• 32支球队，log32=5比特
• 64支球队，log64=6比特

香农指出，它的准确信息量应该是，p为每个球队获胜的概率（假设概率相等，都为1/32），我们不用钱去衡量这个代价了，香浓指出用比特：

1.2.1.1、信息熵的定义

信息熵（Information Entropy）是信息论中的专业术语，其标准单位为比特（bit），用于衡量系统混乱程度的指标。对于一个离散随机变量 X，其可能的取值为 x1​,x2…,xn​，应的概率为P(x1​),P(x2​),…,P(xn​)，则信息熵 H(X)（单位为比特）定义为：

“谁是世界杯冠军”的信息量应该比5比特少，特点（重要）：

• 当这32支球队夺冠的几率相同时，对应的信息熵等于5比特
• 只要概率发生任意变化，信息熵都比5比特大

1.2.1.2、总结

信息和消除不确定性是相联系的：当我们得到的额外信息（球队历史比赛情况等等）越多的话，那么我们猜测的代价越小（猜测的不确定性减小）

• 当所有事件等概率时（最大不确定性），熵值最大，需要更多比特来编码，对应系统混乱，纯度低。

• 当某个事件必然发生时（无不确定性），熵值为0，不需要任何比特编码（因为结果已知)，对应系统稳定，纯度高。

import numpy as np
# 计算信息熵⽰例
p = np.array([39, 37, 44]) / 120 # 概率分布
entropy = -(p * np.log2(p)).sum()
print(f"信息熵: {entropy:.4f}")

问题： 回到我们之前的贷款案例，怎么去划分？可以利用当得知某个特征（比如是否有房子）之后，我们能够减少的不确定性大小。越大我们可以认为这个特征很重要。那怎么去衡量减少的不确定性大小呢?

1.2.2 、信息增益(树划分依据之一)

1.2.2.1 、定义与公式

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

H(D)-数据集D的信息熵（经验熵）：

• K：目标变量中的类别数量