目录

1.简单介绍傅里叶变换的作用

2.谐波是什么

3.解决方法

---

1.简单介绍傅里叶变换的作用

任何复杂的波形归根结底都是由多个频率和相位不一样的正弦波组成的

通过傅里叶变换可以找到组成一个复杂的波形的所有正弦波的频率和幅度信息

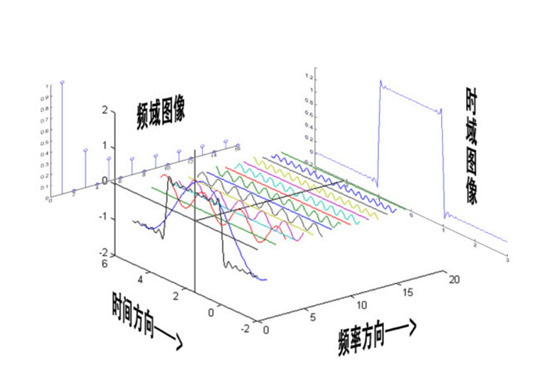
2.谐波是什么

假设有一个复杂的波形，它由多个正弦波有规律的叠加而成，且第一个正弦波频率为5KHz，第二个正弦波为10KHz，第三个正弦波为15KHz……

可以发现后续的正弦波频率都是第一个正弦波的整数倍，所以我们称第一个正弦波为基波（或一次谐波），第二个正弦波为二次谐波，以此类推

使用STM32以合适的频率对这个复杂的波形采样（用数组A存储），并将采样得到的数据利用DSP数学库中的快速傅里叶变换得到新的数据（也用数组B存储），我们该如何正确找出各谐波的幅值呢？

3.解决方法

假设基波的幅值比其他谐波的幅值都要高

我们可以先通过大小比较确定基波（一次谐波）在数组B中的下标N，当我们确定基波在数组B的下标后，由于谐波的频率必然是基波的整数倍，可以通过乘以基波下标的2倍、3倍、4倍……找到二次、三次、四次谐波……的位置是2N、3N、4N……

//假设基波的幅度高于直流分量和后续所有的谐波
//先找基波，假设B数组的长度为size
int i = 0;
int MAX_Location = 0;     //存储最大值所在位置
float MAX = B[0];         
for( i = 0; i < size; i++)
{if( B[i] > MAX ){MAX = B[i];MAX_Location = i;}
}

但这样的方法存在找不准的问题，比如二次谐波幅值实际是2V，由于采样频率问题，2倍的基波数组下标内存储的幅值只有1V，真正的二次谐波在应该在2N-1或者2N+1，那么可以通过在2N的小范围区间内再找一次最大值

当小区间内相邻两个值误差在一定范围内可视为由于采样频率的问题，其实在两者间真正的最大值没有采到，可以人为地在合适的范围修正

int i = 0;
int Number = 0;           //假设有Numer次谐波
int number = Number;
int arr[number] = {0};    //用于存储每个谐波在B数组中的下标
float correction = 30;    //人为修正刚好没有采到最大值，而是采到左右两个值的问题
float max = 0；number = 0;    
for( i = 2; i < Number; i++)	
{	max = B[Base_location * i - 2];            for( j = Base_location * i - 2; j < Base_location * i + 2; j++ )  //取±2的区间{if( fabs(arr[j] - arr[j + 1]) < 30)                           //修正{B[j] = (B[j] + B[j+1]) / 2 + 15;} if( B[j] > max ){max = B[j];arr[number] = j;number++;}}		
}