0. 前言

  Flash Attention可以节约模型训练和推理时间，很多模型可以通过config参数来选择attention是标准的attention实现还是flash-attention方式。在这里记录一下flash attention的学习过程，发现了一位博主以及参考的资料特别好：

• zhihu一位做高性能计算的博主博文
• 华盛顿大学的课程note

1. flash-attention原理简述

$$attention(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$
  标准的attention操作的时间卡点不是在运算上，而是卡在数据读写上。SRAM的读写速度快，但是存储空间有限，无法一次存下来所有的中间计算结果，一次attention计算存在SRAM<->HBM的多次读写操作。

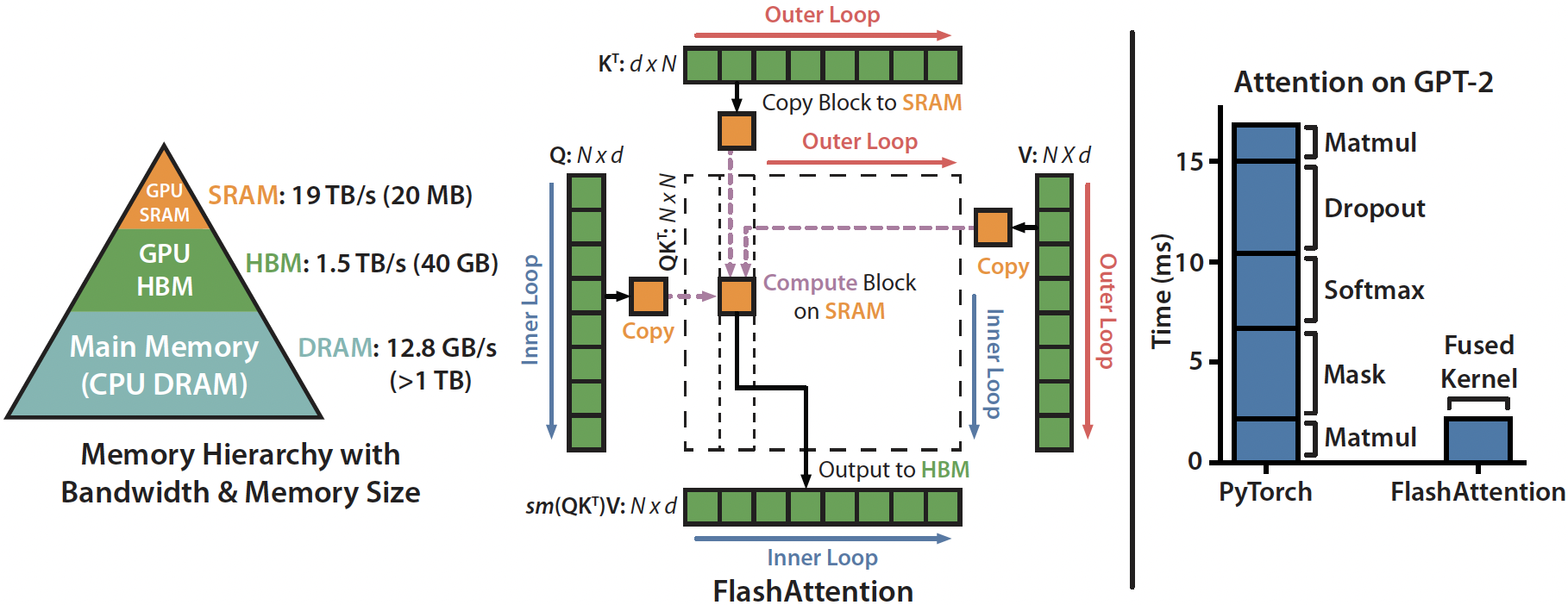
  与标准的attention操作比较，flash-attention通过减少数据在HBM和SRAM间的读写操作，来节约时间(甚至backward时还进行了重新计算，重新计算的速度也比把数据从HBM读取到SRAM要快)。

2. 从softmax到online softmax

  直接看flash-attention的论文比较难看明白，发现华盛顿大学的那份note写得特别清晰，跟着它从softmax看到flash-attention会比较容易。

2.1 safe-softmax

  首先是safe的softmax计算方式。原始的softmax，对于N个数：
s o f t m a x ( { x 1 , . . . , x N } ) = { e x i ∑ j = 1 N e x j } i = 1 N softmax(\{x_1,...,x_N\})=\left\{\frac{e^{x_i}}{\sum_{j=1}^{N}e^{x_j}}\right\}_{i=1}^{N} softmax({x1​,...,xN​})={∑j=1N​exj​exi​​}i=1N​
  对于FP16，最大能表示的数据为65536，当$x>=11$时，$e^x$就会超过FP16的最大表示范围影响结果的正确性。为了避免这个问题，SafeSoftmax 通过减去输入向量中的最大值来调整输入，使得最大的指数项变为$e^0=1$从而防止了上溢的发生。同时，由于所有的指数项都除以同一个数，它们的比例关系不会改变，因此也不会影响最终的概率分布。
e x i ∑ j = 1 N e x j = e x i − m ∑ j = 1 N e x j − m , m = m a x { x j } j = 1 N \frac{e^{x_i}}{\sum_{j=1}{N}e^{x_j}}=\frac{e^{x_i-m}}{\sum_{j=1}{N}e^{x_j-m}}, \quad m=max\left\{x_j\right\}_{j=1}^{N} ∑j=1​Nexj​exi​​=∑j=1​Nexj​−mexi​−m​,m=max{xj​}j=1N​

2.2 3-pass safe softmax

• 对于一个行向量 { x i } i = 1 N \{x_i\}_{i=1}^N {xi​}i=1N​，最直白的softmax计算方式是直接for循环

  这个算法计算softmax需要执行3次从1->N的循环，在attention中， { x i } \{x_i\} {xi​}是$Q{K}^T$的结果，但是如果SRAM里面存不下这个大的矩阵，上面的计算过程，就需要从HBM里面加载3次 { x i } \{x_i\} {xi​}，时间花在了数据读写上。

2.3 Online softmax

  如果能把上面(7)(8)(9)这3个式子的计算放一个for循环，就只需要一次load数据。但是$m_N$是全局最大值，计算$m_N$就已经需要一次遍历了。
  Online softmax算法把(7)(8)进行了合并，把3次遍历缩减为2个。它提出计算$d_i^{\prime }={\sum }_{j=1}^i{e}^{x_j-m_i}$来代替计算$d_i$，当算到最后$i=N$时会发现，$d_N=d_N^{\prime }$。具体的，迭代计算$d_i^{\prime }$的方式为：
$$\begin{array}{rl}{d}_i^{\prime }& =\sum _{j=1}^i{e}^{x_j-m_i}\\ & =\left(\sum _{j=1}^{i-1}{e}^{x_j-m_i}\right)+e^{x_i-m_i}\\ & =\left(\sum _{j=1}^{i-1}{e}^{x_j-m_{i-1}}\right)e^{m_{i-1}-m_i}+e^{x_i-m_i}\\ & =d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}+e^{x_i-m_i}\end{array}$$

  所以就可以用迭代的方式，在找最大值$m_N$的时候，同时来计算$d_i^{\prime }$，把(7)和(8)一起计算，这样只需要加载两次$x_i$。

2.4 Flash-attention

  上面的online softmax仍然需要2个for循环，加载2次$x_i$来完成softmax的计算。完成softmax的计算，没法更进一步地压缩到1次遍历。但是attention计算的最终目标是获取输出结果，也就是注意力分数与$V$相乘的结果$O=A\times V$，计算$O$可以通过一次遍历完成。

  可以使用类似online softmax把计算$d_i$变成计算$d_i^{\prime }$的方式，把$o_i$的计算也改成迭代式的，首先把$a_i$带入$o_i$的表达式
$$o_i=\sum _{j=1}^i\left(\frac{e^{x_j-m_N}}{d_N^{\prime }}V[j,:]\right)$$

  可以找到一个$o_i^{\prime }$，它不依赖于全局的$d_N^{\prime }$和$m_N$
$$o_i^{\prime }=\sum _{j=1}^i\left(\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:]\right)$$

  对于$o_i^{\prime }$的计算可以使用迭代的方式，同样的是有$o_N=o_N^{\prime }$
$$\begin{array}{rl}{o}_i^{\prime }& =\sum _{j=1}^i\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime }}\frac{e^{x_j-m_i}}{e^{x_j-m_{i-1}}}\frac{d_{i-1}^{\prime }}{d_i^{\prime }}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime }}V[j,:]\right)\frac{d_{i-1}^{\prime }}{d_i^{\prime }}{e}^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & =o_{i-1}^{\prime }\frac{d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}}{d_i^{\prime }}+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\end{array}$$

  这样计算attention的输出结果可以只进行一次遍历就完成

2.5 Flash-attention tiling

  上面是每次计算一个元素$[i]$，实际上可以一次读取一个大小为b的块(tile)来计算

  此外，在flash-attention的paper里面，对$Q$、$K$、$V$和$O$分块，其中$Q$
和$O$每块大小为$min(M/4d,d)\times d$，$K/V$的每块大小为$M/4d\times d$，加起来正好不会超过SRAM的大小M，完整的算法在paper中：