信号(瞬时)频率求解与仿真实践(2)

引言

本文是信号(瞬时)频率求解与仿真实践专题的第二篇文章，在上一篇博文 [1]信号(瞬时)频率求解与仿真实践(1)-CSDN博客中，我构建了信号瞬时频率求解的基本框架，并且比较详细地讨论了瞬时频率法。这篇博文探讨适用于信号瞬时频率求解的另一种方法：联合时频分析(对应博文[1]的第3.2节)。

本文将给出几种典型的联合时频分析法，对其理论做介绍，并实践：对仿真得到的回波信号以及雷达的实测数据进行联合时频处理。(各联合时频分析法的具体实现，Matlab都有自带的函数，本文提供的代码将直接调用这些函数，本文重点不是如何自编代码实现这些联合时频算法。)

Blog

2025.6.13 本文第一次撰写

一、联合时频分析法概述以及几种典型算法

1.1 概述

联合时频分析法是求解信号瞬时频率的另一种解决思路(还有一种前文介绍的瞬时频率分析法)，它不需要求解信号的相位以及做多分量信号的分解，而是同时在时间和频率维度处理信号，并可以直接给出信号在二维的时间-频率域的能量分布。该方法很早就被用来分析时变频谱，其不仅可用于单分量信号也可以直接用于多分量信号的时频分析。

联合时频分析法可以进一步被分为：线性时频变换和双线性时频变换。短时傅里叶变换(Short-time Fourier Transform，STFT)就是典型的线性时频变换法，常见的双线性时频变换如：维格纳-维利分布（Wigner-Ville distribution，WVD）以及在其基础上的各类改进算法。

本章将介绍几种常用的联合时频分析法。

1.2 短时傅里叶变换(short time fourier transform, STFT) 及其拓展

短时傅里叶变换是线性时频率变换的一种，也是最常用的联合时频分析法。STFT的数学表达式如下：

（1-1）

式中，x(t)是待处理信号，w(t-τ)是窗函数。与FFT直接对信号在整个时间维度进行处理相比，STFT的本质是通过设置特定的窗函数将信号分割成很多个短的时间段，随后对每个时间段进行FFT处理，最后将各个时间段处理的结果进行排序从而得到信号的二维时频分布。STFT最大的缺点是需要在时间分辨率和频率分辨率之间做取舍：更长的时间段可以获得更好的频率分辨率，但是牺牲了时间分辨率，反之亦然。在一些特定的应用场景下，考虑到当目标速度的变化周期在时间维度发生变化时，固定窗函数下可能无法准确捕捉其速度特征，也有文章[2]提出了基于信号周期的自适应窗函数下的STFT处理：在STFT过程中，将信号分成时间间隔不相等的几段进行FFT处理。

虽然STFT下的分辨率受限，但是该方法计算简单也不会引入干扰项，所以依然是时频分析里面应用最广泛的方法。

我们把STFT处理得到的数据矩阵取幅值后称之为Spectrogram。在STFT得到Spectrogram谱图的基础上，还有一些更进一步的处理方法得到新的谱图，常用的如：Candence Velocity Diagram（CVD）[3]和Cepstrogram[4],这两谱图都是在STFT的结果上做进一步的处理得到的，其关系如下图所示[5]：

图1.1 Spectrogram、CVD、Cepstrogram三种谱图的关系

CVD谱图是在Sepctrogram的基础上取对数(自然对数和以10为底的对数都可)，然后对每个频率点求时间维度的FFT得到。CVD谱图中包含了时频域中曲线的重复情况，提供了关于目标运动部件在时频图中曲线的形状、大小和频率的信息。 Cepstrogram也是在Sepctrogram的基础上取对数(自然对数和以10为底的对数都可)，不过随后是对每个时间点求频率维度的IFFT得到，Cepstrogram谱图中包含了时频谱的周期性信息。如上图所示，这三种谱图在很多的文献中被用于做微动特征的提取(Feature extraction)或者直接作为样本输入到CNN等深度学习网络中进行训练和目标识别。

Matlab中有自带的函数：spectrogram 可以实现STFT功能，这里不做过多介绍。

1.3 Wigner-Ville分布(Wigner-Ville distribution， WVD)及其拓展

为了提高时频分辨率，一些双线性时频变换方法被提出。WVD就是其中最简单以及最有代表性的方法，WVD是通过计算信号自相关函数的傅里叶变换得到，表达式如下：

(1-2)

式中τ是时移变量(在t的基础上做时移)，s*表示复共轭，是信号在时间t附近的局部自相关，其衡量了信号在时间t附近的相似度，在此基础上进行傅里叶变换可以得到信号在时间t附近的频率分布。这种方法的时频分辨率远高于线性时频变换，但是计算复杂度高，且受到交叉项干扰：如果信号中有多个频率信息，此时对多个频率信号和的WVD并不等于对各个频率信号WVD的和，也就是说，如果信号中包含多个频点，那么WVD处理后会有交叉项，而且交叉项对应的幅值要高于各个频率分量，如果不做抑制，会产生错误的时频谱图，影响后续处理。

为了抑制该交叉项的干扰，需要进行滤波处理。不同的滤波方法(基于核函数)就有了不同的双线性时频分析方法，如下表所示[6]：

图1.2 各双线性时频分析法及其核函数

以比较常见的平滑伪wigner-ville分布(Smooth Pseudo WVD,SPWVD)为例，其在WVD的基础上引入频域平滑窗h(τ)和时域平滑窗g(s-t)，来减少交叉项的干扰：

(1-3)

窗函数的引入虽然可以抑制交叉项的干扰，但是会影响时间分辨率（窗越宽，交叉项越少，但是时间分辨率也会越低）。

1.4 小波变换（wavelet Transform, WT）

小波变换也是一种常见的时频分析方法，不同于傅里叶变换中使用正弦函数作为基函数对信号进行分解，小波变换使用可变尺度的基函数(小波)在时频域上对信号进行分析，其可以很好地解决STFT无法同时兼顾时间和频率分辨率的缺点。有关小波变换更形象的理解可以参考资料[7]。

小波变换使用母小波ψ(t)通过平移和缩放生成一组小波基：

(1-4)

式中，a是尺度参数，可以控制频率。B是平移参数，可以控制时间位置，常见的母小波如：morlet波、haar波等。连续小波变换公式如下：

（1-5）

小波变换没有分辨率的限制，适合精细分析，但是该方法计算量大，冗余信息多，而且选定了母小波后，在整个分析过程中将无法更换，即使该母小波在全局可能是最佳的，但在某些局部可能并不是，所以小波分析的基函数缺乏适应性。

1.5 其它方法

A. Capon变换（或称为最小方差无失真响应，Minimum Variance Distortionless Response，MVDR）

Capon变换是一种典型的超分辨率波束形成算法(我在很早前的车载毫米波雷达DOA估计研究[8]中讨论过该算法)，将之引入时频分析，其实原理与测角是类似的：把所采集的时域信号理解成测角时的各通道采集的信号即可。其实现过程可以分为四步：

1、信号分段(类似STFT中设置时间窗，把原始信号分成很多的小段)；

2、对每段信号，计算其自相关矩阵R(信号的协方差矩阵)

3、构造频率导向矢量：

4、对于每个频点，计算该特定时间段和特定频点下的Capon值：

通过对每段信号进行前述步骤2到4的处理，便可以得到Capon变换下的时频图。Capon方法下相较于STFT、WVD等方法有更高的频率分辨率(时间分辨率没有太多改善)，且无交叉项干扰，但是该方法需要耗费较大的计算资源，而且基于单段信号计算得到的协方差矩阵可能误差较大、求逆不稳定，算法的抗噪以及稳定性较差。

B. 联合时频分析算法当然远不止上面几种，不过上面几种是我在课题相关的专业文献中遇到使用比较多的几种。后续如果碰到有其它比较常见的算法我再做补充。

二、本文的仿真信号参数以及实测数据集介绍

本章对待处理的信号做介绍。本文的实践中，我预设了一份比较理想的仿真信号、以及使用了一份实测数据集中的信号分别实践各联合时频处理算法。

2.1 仿真信号参数介绍

仿真的信号设置为两个chirp信号的叠加，其参数列表如下：

表2.1 仿真信号参数列表

参数	Chirp1	Chirp2
起始频率	0	200Hz
调频斜率	100Hz/s	-50Hz/s
采样率(双路采样)	600Hz
采样点数	1024
采样时间	1.7067s
计算得到终止频率	170.67Hz	114.67Hz
噪声	SNR=20dB的高斯白噪声

这是一个典型的多分量且频率时变信号，在本系列上一篇文章[1]中，我们使用希尔伯特-黄变换处理过类似的信号，但是效果不佳。

信号的时域以及直接FFT处理的结果如下：

图2.1 仿真信号时域

图2.2 仿真信号直接进行FFT处理的结果

从上图可以看到，信号频段主要位于0至200Hz之间，而且在大约110Hz至170Hz频段内能量比较大，这刚好是我们设置的两信号分量的频段重叠区域。综上可知，信号的频段表现与预设信号参数是吻合的。

2.2 实测数据集数据简介

实测数据我选取了自己课题方向相关的一份雷达探测无人机的数据集。(我在之前的博文[9]中做过雷达测量人体运动的回波时频图处理，感兴趣的读者也可以下载博文[9]中的数据集进行处理)。

本文使用的这份数据集读者可以从信号处理学报的官网上找到下载链接[10]：数据集，与这份数据集相对应的文章是[11],文中有关于该数据集的详细介绍：实验对象、实验场景、数据文件使用说明等，作者在文中还给出了一些基于本数据集的处理示例。本文就不对该数据集做细节的介绍了，本文后续的实践只是取出其中一部分数据做时频处理(在后文的代码链接中，我一并附上了后续章节使用的(从其原始数据中解析出来的原始回波数据的)二维数据矩阵（.mat格式），读者直接load即可，当然我也附上了数据解析和预处理相关的代码。下表为该数据集所使用雷达的主要参数：

表2.2 实测数据集雷达参数列表

参数	值
载频	3.13344GHz
收发通道数	1T8R
工作体制	调频连续波
发射带宽	120MHz
脉冲宽度	2.0835微妙
脉冲重复周期	533.3或1000微秒
中频采样频率	491.52MHz

本文后续的实践部分，我分别选取了无人机悬停（选用其数据集Data3文件夹下的前八个数据文件）和无人机运动两种飞行状态下（选用其数据集Data1文件夹下的前八个数据文件）各一份数据进行时频处理。

其单份小文件下的数据量是：8*128*8192，8对应的是8个接收通道，8192对应单个chirp下距离维采样点数，128对应这份数据文件下包含了128个chirp。【虽然其真值文件中给出了目标的角度，但是其数据说明文档中没有给出接收阵列的排布方式，所以我在做处理时没有使用数字波束形成的方法去增加目标的SNR,而是直接只使用其中一个通道的数据】，此外，所选用的8个小数据文件其实前后是时间连续的，所以这八个数据文件可以在chirp维度连接起来。综上，经过数据解析和排布，得到了两个(分别对应无人机悬停和飞行)大小为：1024*8192 的原始回波数据矩阵(这两份数据我保存为.mat格式，一并附在代码链接中，读者可以直接load后使用，而不用跑数据解析部分的代码)

随后对该矩阵进行：匹配滤波(距离维压缩) --- MTI（去除静态杂波） ---- 多普勒维FFT处理（得到RD图） ---- 找到目标所在距离门 ---- 取出MTI后的数据矩阵中目标所在距离门下的数据进行时频处理

注：实践中发现，对于无人机悬停的情况(此时机身运动速度为0)，即便进行MTI处理也还是可以从RD图中看到无人机回波，而不做MTI处理，后续时频处理后机身的能量很大，会淹没很多的旋翼微动信息。【读者可以基于我提供的代码做更一些对比分析，(直接把代码中MTI处理的部分关闭即可)】

1. 无人机悬停状态下所获取数据的预处理结果

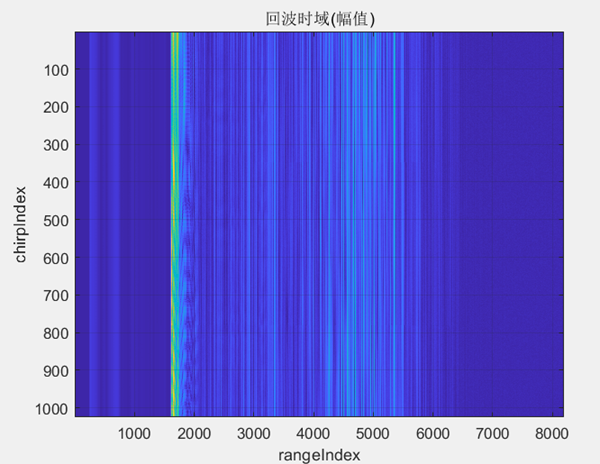
图2.3 回波时域幅值(一共1024个脉冲)

图2.4 回波时域(取其中一个脉冲)

随后对其进行匹配滤波处理，得到：

图2.5 距离压缩后的结果

同样，取其中一个脉冲画图：

图2.6 距离压缩后的结果(取其中一个脉冲)

从图中可以看到杂波很强，并没有明确的目标位置。对距离压缩后的结果做MTI（有关静止目标滤除的方法，读者可以参考我之前的博文[12]）,得到结果如下：

图2.7 距离压缩后的结果MTI后

此时可以看到在距离索引[1400 1900]之间能量比较高，可以认为目标就在该区间内。进一步地，对MTI后的结果再做脉冲维的FFT处理，得到距离-多普勒图(RD图)如下：

图2.8 回波数据矩阵对应的RD图

在这份数据集的说明文档中，Data3对应的实验场景为无人机处于悬停状态，其与雷达之间的斜距约为212.83m，这与上图的结果基本吻合。

【注：图中之所以在速度维度有周期性的波峰，这是无人机旋翼旋转产生的所谓HERM line：当叶片旋转时，叶片会对雷达电磁波产生周期性调制（本质就是微多普勒信号）。如果解调时间窗很长(上面我们用到了全部1024个脉冲)就会产生上图中的HERM line（包括很多的谐波）；如果解调时间窗比较短，会出现所谓的blade flash(在后文的时频处理中会看到)，我们可以从时频图中看到叶片产生的类似正弦信号的调制波形。 进一步地，我们可以从这两种图中获取很多的无人机参数信息，如：叶片旋转速率、叶片长度、旋翼个数等参数。不过这些内容不在本文的讨论范围之内】

在后文的时频处理中，我选取了MTI处理后的距离索引为[1400 1500]区间内的数据做处理。

2. 无人机运动状态下所获取数据的预处理结果

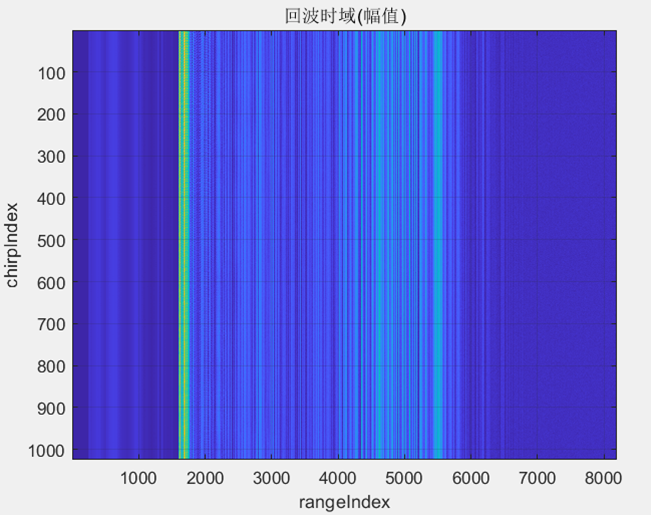
图2.9 回波时域幅值(一共1024个脉冲)

图2.10 回波时域(取其中一个脉冲)

随后对其进行匹配滤波处理，得到：

图2.11 距离压缩后的结果

图2.12 距离压缩后的结果(取其中一个脉冲)

MTI处理后得到：

图2.13 距离压缩后的结果MTI后

进一步地，得到距离-多普勒图(RD图)如下：

图2.14 回波数据矩阵对应的RD图

在这份数据集的说明文档中，Data1对应的实验场景为无人机处于由近及远以S型轨迹飞行的状态，速度约5.8m/s，其与雷达之间的斜距约为250.41m，这与上图的结果基本吻合(速度的绝对值有一些差异，可能是其真值测量不准确？？)。

在后文的时频处理中，我选取了MTI处理后的距离索引为[1550 1650]区间内的数据做处理。

三、基于各联合时频分析算法的实践

本章给出各联合时频分析算法对第二章所介绍的仿真信号以及实测数据的处理结果。 (相关的实现代码可参考第六章给的代码链接)。

本章的处理结果图较多，在实测数据处理部分，我后文提供的代码都会同时输出纵轴分别为频率和速度的两幅图，不过在本文给的结果中，我只选取了其中一幅(而且也没有统一)。

本章的处理结果不一定是最优的，各类时频处理方法中有很多的参数可调节，读者可以基于后文提供的代码自行设置和优化参数。

3.1 STFT处理结果

A. 仿真数据处理结果

STFT的处理参数为：时间窗长64，前后时间窗的重叠率为90%，加汉宁窗。

图3.1 STFT对仿真数据的处理结果

结果是符合2.1节中的预设参数的。

B．实测数据处理结果(目标悬停)

预设时间窗长为16，前后窗的重叠率为0.9，得到结果如下：

图3.2 STFT对实测数据(目标悬停)的处理结果（blade flash图）

还是可以看到一些由叶片旋转引起的周期性的变化？此外，通过把窗长增加到128，可以看到HERM line图：

图3.3 STFT对实测数据(目标悬停)的处理结果（HERM line图）

这些沿速度维排布的能量较大的线条就是所谓的HERM line图，这与我们在前面得到RD-mat类似。

C．实测数据处理结果(目标运动)

预设时间窗长为16，前后窗的重叠率为0.9，得到结果如下：

图3.4 STFT对实测数据(目标悬停)的处理结果（blade flash图）

可以看到速度为-5到-10之间能量很强，对应机身的运动。在-15周围也有一些周期性出现的能量强点，这些对应的就是旋翼。通过把窗长增加到128，可以看到HERM line图：

图3.5 STFT对实测数据(目标悬停)的处理结果（HERM line图）

3.2 CVD谱图

A. 仿真数据处理结果

经由图3.1的结果处理而来：

图3.6 对仿真数据处理得到的CVD图

似乎看不到什么有用的信息。

B．实测数据处理结果(目标悬停)

设置STFT的窗长为16，在STFT的结果上处理得到(这里采用取自然对数的方式实现)：

图3.7 对目标悬停状态下回波处理得到的CVD图

结果暂不做评价。读者可以基于后文提供的代码尝试设置不同的STFT参数，以及取以10为底的对数，或者对整个STFT的结果先做归一化处理再进行1.2所介绍的CVD处理。看看是否有其它更好的结果。

C．实测数据处理结果(目标运动)

图3.8 对目标运动状态下回波处理得到的CVD图

3.3 cepstrogram谱图

A. 仿真数据处理结果

经由图3.1的结果处理得到：

图3.9 对仿真数据处理得到的Cepstrogram图

似乎看不到什么有用的信息。

B．实测数据处理结果(目标悬停)

设置STFT的窗长为16，在STFT的结果上处理得到(这里采用取自然对数的方式实现)：

图3.10 对目标悬停状态下回波处理得到的Cepstrogram图

结果暂不做评价。

C．实测数据处理结果(目标运动)

设置STFT处理时的窗长为128，得到结果如下：

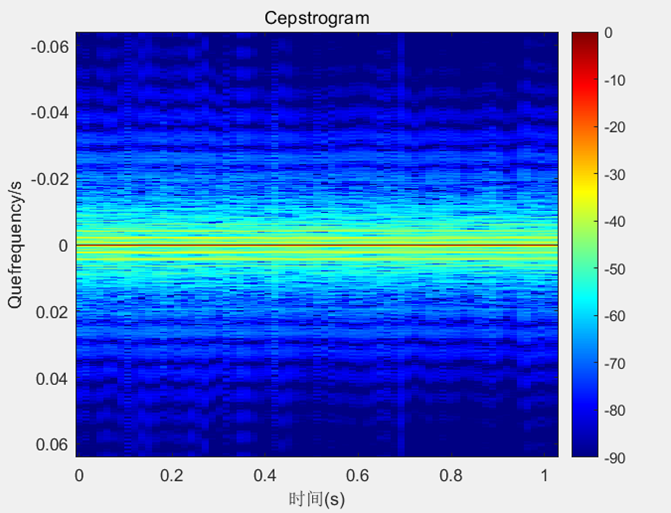
图3.11 对目标运动状态下回波处理得到的Cepstrogram图

3.4 WVD&SPWVD

A. 仿真数据处理结果

图3.12 对仿真数据做WVD处理的结果

虽然可以看到预设频率下的信号，但是整个时频图中有比较强烈的干扰。随后预设时间和频率窗长都为129，得到SPWVD的处理结果如下：

图3.13 对仿真数据做SPWVD处理的结果

可以看到交叉干扰项确实得到了有效抑制。读者可以基于给的代码设置其它长度的窗长看看效果。

B．实测数据处理结果(目标悬停)

图3.14 对目标悬停状态下的回波数据做WVD处理的结果

WVD无法输出负频带的信息，这部分信息会被耦合到正频带中。设置时间和频率窗的长度都是127，得到SPWVD的处理结果如下：

图3.15 对目标悬停状态下的回波数据做SPWVD处理的结果

C．实测数据处理结果(目标运动)

图3.16 对目标运动状态下的回波数据做WVD处理的结果

设置时间和频率窗的长度都是127，得到SPWVD的处理结果如下：

图3.17 对目标运动状态下的回波数据做SPWVD处理的结果

这两种方式处理得到的时频图比较接近STFT处理的结果。

3.5 小波变换处理结果

本节的处理中都使用’morse’小波基函数。

A. 仿真数据处理结果

图3.18 CWT变换对仿真数据的处理结果

可以看到与STFT变换类似的效果，但是动态范围低很多。(注意频率范围的变化？)

B．实测数据处理结果(目标悬停)

图3.19 CWT变换对实测数据(目标悬停)的处理结果

C．实测数据处理结果(目标运动)

图3.20 CWT变换对实测数据(目标运动)的处理结果

还是可以看到在速度为5m/s左右有一条能量较大的曲线。

3.6 Capon算法处理结果

本节的仿真中，都预设窗长为64，前后时间段移动16点，频率点数为256点。

A. 仿真数据处理结果

图3.21 Capon算法对仿真数据的处理结果

效果与STFT的处理结果类似，不过SNR要低一些。

B．实测数据处理结果(目标悬停)

图3.22 Capon算法对实测数据(目标悬停)的处理结果

C．实测数据处理结果(目标运动)

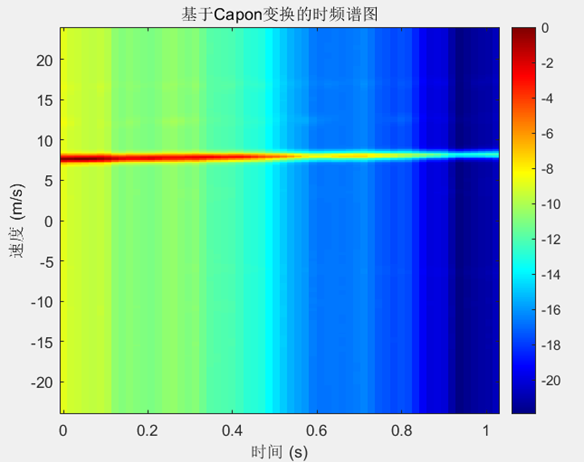
图3.23 Capon算法对实测数据(目标运动)的处理结果

可以看到其准备捕捉到了目标的运动速度，不过没有旋翼转动引起的速度调制等细节。

四、总结

时频图的获取往往并不是我们的最终目的，时频图是一种很好的、可用于分析雷达目标的媒介。一般来说，获取时频图主要有三个目的：一是从图中提取所需的目标参数信息(比如无人机旋翼数量、叶片长度、叶片旋转频率等参数)；二是从时频图中提取一些特征，以供给后续的传统机器学习算法；三是将时频图直接给到深度学习网络中进行训练并完成目标识别等任务。

本文作为信号(瞬时)频率求解与仿真实践话题下的第二篇文章，主要介绍并实践了几种典型的联合时频处理算法。

五、参考资料

[1] 信号(瞬时)频率求解与仿真实践(1)-CSDN博客

[2] D. B. Herr and D. Tahmoush, "Data-Driven STFT for UAV Micro-Doppler Signature Analysis," 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 2020, pp. 1023-1028, doi: 10.1109/RADAR42522.2020.9114726.

[3] S. Björklund, T. Johansson, and H. Petersson, “Evaluation of a micro Doppler classification method on mm-wave data,” in Proc. IEEE Radar Conf., May 2012, pp. 934–939.

[4] A. M. Noll and M. R. Schroeder, “Short-time ‘cepstrum’ pitch detection,” J. Acoust. Soc. Amer., vol. 36, no. 5, p. 1030, 1964, doi: 10.1121/1.2143271.

[5] A. Hanif, M. Muaz, A. Hasan and M. Adeel, "Micro-Doppler Based Target Recognition With Radars: A Review," in IEEE Sensors Journal, vol. 22, no. 4, pp. 2948-2961, 15 Feb.15, 2022, doi: 10.1109/JSEN.2022.3141213.

[6] V. C. Chen, F. Li, S. . -S. Ho and H. Wechsler, "Micro-Doppler effect in radar: phenomenon, model, and simulation study," in IEEE Transactions on Aerospace and Electronic Systems, vol. 42, no. 1, pp. 2-21, Jan. 2006, doi: 10.1109/TAES.2006.1603402.

[7] https://zhuanlan.zhihu.com/p/22450818

[8] 车载毫米波雷达DOA估计综述-CSDN博客

[9] 雷达一维成像：基于数据集的实践-CSDN博客

[10] 数据集

[11] 林钱强, 秦正阳, 蒋李兵, 等. 简单野外背景条件下地面雷达对“低慢小”无人机探测数据集[J]. 信号处理, 2024, 40(11): 2095-2104. DOI: 10.12466/xhcl.2024.11.014.

[12] 毫米波雷达信号处理中的静止目标(静态杂波)滤除问题-CSDN博客