零、题目描述

题目链接： LCR 130.衣橱整理（注：LCR 130 与剑指 Offer 13 相同）

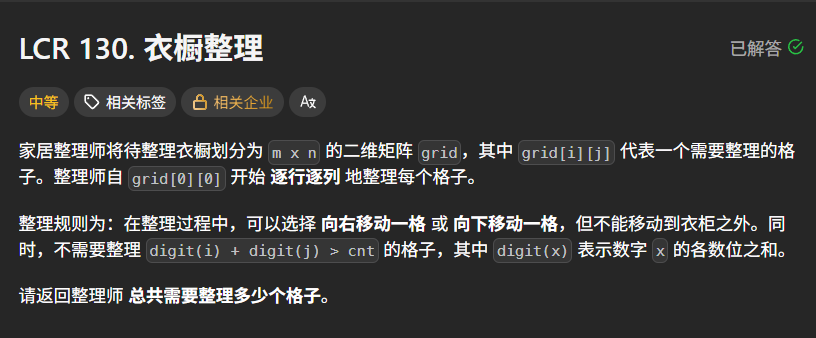
示例 1：
输入：m = 4, n = 7, cnt = 5
输出：18

示例 2：
输入：m = 2, n = 3, cnt = 1
输出：3
解释：
满足条件的格子坐标为 (0,0)、(0,1)、(1,0)。

• (0,0)：数位和 0+0=0 ≤ 1
• (0,1)：数位和 0+1=1 ≤ 1
• (1,0)：数位和 1+0=1 ≤ 1
• (0,2)：数位和 0+2=2 > 1（不满足）
• (1,1)：数位和 1+1=2 > 1（不满足）
• (1,2)：数位和 1+2=3 > 1（不满足）

一、为什么这道题值得一看？

这道题是网格搜索问题的经典变种，核心围绕“带条件的路径探索”展开，能帮你深化对深度优先搜索（DFS）在约束场景下的应用理解。

它的独特价值在于：

1. 固定起点的探索：不同于需要遍历多个起点的问题，本题仅从 (0,0) 出发，更聚焦于“单起点扩散”的逻辑；
2. 有限移动方向：只能向右或向下移动，需要针对性设计搜索路径，避免无效探索；
3. 自定义过滤条件：通过数位和判断是否访问格子，增加了搜索过程中的“筛选”环节，考验条件整合能力。

通过本题，你能掌握：

• 如何在 DFS 中嵌入自定义判断条件（如数位和计算）；
• 如何处理网格中的边界与访问标记；
• 单起点、有限方向场景下的搜索逻辑设计。

对DFS（深度优先搜索）和洪水灌溉算法感兴趣的朋友，不妨看看我的每日一题专栏。专栏里，在本篇之前的内容已经围绕这两个主题做了层层铺垫——从基础的递归逻辑、网格遍历，到洪水灌溉的核心思想，每一步都有细致的拆解和代码解析。

而今天这篇，更像是对“洪水灌溉”系列问题的一次总结收尾。因此，代码层面不会再做过于细致的逐行讲解（那些细节在前几篇中已有充分覆盖），重点会放在思路的梳理和这类问题的共性规律上，帮你形成完整的解题框架~

二、题目拆解：核心要素与约束

核心目标
统计从 (0,0) 出发，通过向右或向下移动可到达的、且满足 digit(x) + digit(y) ≤ cnt 的格子总数（包含起点）。

关键要素解析

1. 数位和计算：
   需实现函数 digit(x)，计算数字 x 的各数位之和。例如：x=12 时，1+2=3；x=0 时，结果为 0。

2. 移动规则：
   每次移动只能选择两个方向：

   • 向右：(x, y) → (x, y+1)
   • 向下：(x, y) → (x+1, y)

3. 访问条件：
   一个格子 (x, y) 可被访问，需同时满足：

   • 坐标在网格内：0 ≤ x < m 且 0 ≤ y < n；
   • 未被访问过（避免重复计数）；
   • 数位和满足：digit(x) + digit(y) ≤ cnt。

4. 计数逻辑：
   每访问一个满足条件的格子，就将计数器加 1，最终返回计数器的值。

三、算法实现：基于 DFS 的解决方案

完整代码

class Solution {
public:// 方向数组：向右（0,1）、向下（1,0）int dx[2] = {0, 1};int dy[2] = {1, 0};// 标记已访问的格子，避免重复计数bool visited[100][100] = {false};// 计数变量：记录满足条件的格子总数int count = 0;// 网格大小与数位和阈值（全局变量，避免参数传递冗余）int m, n, cnt;int wardrobeFinishing(int _m, int _n, int _cnt) {m = _m;n = _n;cnt = _cnt;// 先检查起点是否满足条件if (digit(0) + digit(0) > cnt) {return 0;}// 标记起点为已访问，启动DFSvisited[0][0] = true;dfs(0, 0);return count;}// DFS：从(x,y)出发，探索所有可达的有效格子void dfs(int x, int y) {// 访问当前格子，计数+1count++;// 尝试两个方向的移动for (int i = 0; i < 2; i++) {int nx = x + dx[i];  // 新行坐标int ny = y + dy[i];  // 新列坐标// 检查新坐标是否满足所有条件if (isValid(nx, ny)) {visited[nx][ny] = true;  // 标记为已访问dfs(nx, ny);             // 递归探索}}}// 辅助函数：判断(nx, ny)是否可访问bool isValid(int nx, int ny) {// 条件1：在网格边界内if (nx < 0 || nx >= m || ny < 0 || ny >= n) {return false;}// 条件2：未被访问过if (visited[nx][ny]) {return false;}// 条件3：数位和满足要求if (digit(nx) + digit(ny) > cnt) {return false;}return true;}// 辅助函数：计算数字x的数位和int digit(int x) {int sum = 0;while (x > 0) {sum += x % 10;  // 累加最后一位x /= 10;        // 移除最后一位}return sum;}
};

代码逻辑拆解

1. 方向数组设计
由于只能向右或向下移动，方向数组定义为：

• dx[0] = 0, dy[0] = 1 → 向右移动（行不变，列+1）
• dx[1] = 1, dy[1] = 0 → 向下移动（行+1，列不变）

2. 数位和计算（digit(x))

• 功能：将数字 x 拆分为各个数位，返回总和。
• 实现逻辑：通过 x % 10 取最后一位，累加至 sum，再通过 x /= 10 移除最后一位，循环至 x = 0。
• 示例：x=23 时，23%10=3，x=2；2%10=2，x=0，总和为 3+2=5。

3. 有效性判断（isValid(nx, ny)）
整合三大条件的判断，避免在 DFS 中重复写逻辑：

• 边界检查：确保 (nx, ny) 处于网格内；
• 访问检查：通过 visited 数组判断是否已访问；
• 数位和检查：计算 digit(nx) + digit(ny) 并与 cnt 比较。

4. DFS 递归流程

1. 进入 dfs(x, y) 后，先将当前格子计入总数（count++）；
2. 遍历两个移动方向，计算新坐标 (nx, ny)；
3. 通过 isValid(nx, ny) 检查新坐标是否可访问；
4. 若可访问，标记为已访问并递归调用 dfs(nx, ny)，继续探索。

5. 起点特殊处理
在启动 DFS 前，需先判断起点 (0,0) 的数位和是否满足条件。若不满足（如 cnt < 0），直接返回 0，无需执行 DFS。

五、时间复杂度与空间复杂度

时间复杂度

• 网格访问：每个格子最多被访问一次，共 m×n 个格子；
• 数位和计算：对每个坐标 (x,y)，数位和计算时间为 O(log x + log y)（x 最大为 m-1，y 最大为 n-1）；
• 总复杂度：O(m×n×(log m + log n))，可简化为 O(m×n)（因 log m 和 log n 为常数级）。

空间复杂度

• 递归栈：最坏情况下（所有格子均有效），递归深度为从 (0,0) 到 (m-1,n-1) 的路径长度，即 O(m + n)；
• 访问标记数组：visited 为固定大小的 100×100 数组，空间复杂度为 O(1)；
• 总复杂度：O(m + n)。

六、坑点总结

1. 数位和计算错误：

   • 忽略 x=0 的情况：digit(0) 应返回 0，若循环条件写为 x >= 0 会导致死循环（x=0 时 x%10=0，x/10=0，无限循环）。
   • 错误处理负数：题目中 x 为坐标（非负），无需考虑负数，但需确保函数对非负整数有效。

2. 方向数组设计错误：
   误加入向左或向上的方向，导致访问无效格子或重复计数（如 (0,0) 向左移动到 (0,-1) 会越界）。

3. 未标记已访问：
   虽然移动方向固定（右/下），理论上不会重复访问，但特殊场景下（如 m=1, n=1）可能出错，需严格标记访问状态。

4. 起点判断遗漏：
   未提前检查起点是否满足条件，导致 (0,0) 无效时仍启动 DFS，计数错误（如 cnt=-1 时，错误返回 1）。

七、举一反三

掌握本题逻辑后，可尝试解决以下类似问题：

• LeetCode 62. 不同路径：计算从 (0,0) 到 (m-1,n-1) 的路径总数（无过滤条件，仅统计路径数）；
• LeetCode 63. 不同路径 II：在 62 题基础上增加障碍物，需在搜索中过滤障碍格子；
• 剑指 Offer 13. 机器人的运动范围：与本题完全一致，仅表述不同。

八、洪水灌溉（Flood Fill）系列问题总结

回顾这几天的5篇博客，从岛屿数量到今天的 衣橱整理，我们围绕洪水灌溉（Flood Fill）算法展开了一系列递进式学习。这些题目虽场景各异，但核心逻辑一脉相承，又在细节上层层深入，共同构成了对网格搜索问题的完整认知。

1.共性：洪水灌溉的核心框架
所有题目都围绕 “连通区域遍历与标记” 展开，共享以下核心逻辑：

1. 遍历触发：从特定起点（或多个起点）出发，触发深度优先搜索（DFS）或广度优先搜索（BFS）；
2. 方向探索：通过方向数组（4方向、8方向等）遍历相邻单元格，模拟“洪水扩散”；
3. 访问标记：通过原地修改（如将1改为0）或额外数组标记已访问区域，避免重复处理；
4. 边界控制：严格检查坐标合法性（是否在网格范围内），防止越界。

2.递进：从基础到进阶的能力拆解

(1) 基础：连通区域的“计数”与“计量”

• LeetCode 200. 岛屿数量：入门级题目，核心是“统计连通区域数量”。通过4方向DFS遍历，每发现一个未标记的陆地（1）就计数，并“淹没”整个岛屿（标记为0）。这是洪水灌溉的最基础形态，教会我们“如何识别并标记一个完整的连通区域”。
• LeetCode 695. 岛屿的最大面积：在计数基础上升级为“计量区域规模”。同样用4方向DFS，但新增“面积累加”逻辑（每次访问陆地时累加计数），并跟踪最大值。这一步让我们学会“在遍历中携带并更新数据”。

(2)进阶：思维反转与复杂条件

• LeetCode 130. 被围绕的区域：引入“反向标记”思维。不再直接寻找“被围绕的区域”，而是从边界出发标记“不被围绕的安全区”（与边缘连通的O），最后通过排除法处理目标区域。这一步打破了“正向搜索”的固定思维，学会“正难则反”的策略。
• LeetCode 417. 太平洋大西洋水流问题：进一步深化反向思维。通过双标记数组（分别记录能流向两大洋的区域），从海洋边界“逆流”标记可达区域，最终取交集。这题训练了“多目标标记与结果整合”的能力。

(3)拓展：方向与条件的灵活适配

• LeetCode 529. 扫雷游戏：扩展遍历方向至8方向（含对角线），并新增“条件终止”逻辑（根据周围地雷数决定是否继续扩散）。这题让我们学会“根据场景调整探索范围”和“动态控制递归深度”。
• LCR 130. 衣橱整理：加入“自定义过滤条件”（数位和判断），且限制移动方向为2方向（右/下）。这题展示了洪水灌溉在“带约束的单起点扩散”场景中的应用，强调“条件过滤与方向限制”的结合。

3.收获：从“会用”到“会变通”
通过这一系列题目，我们不仅掌握了洪水灌溉的基础框架，更理解了“算法复用与变体适配”的核心思维：

• 不变的是框架：无论场景如何变化，“遍历触发→方向探索→访问标记→边界控制”的流程始终是核心，掌握这一点，就能应对80%的网格搜索问题；
• 可变的是细节：根据题目目标调整“起点选择”（单起点/多起点/边界起点）、“方向范围”（4方向/8方向/有限方向）、“过滤条件”（无限制/数位和/高度差等）、“目标输出”（计数/计量/标记/交集），就能将基础框架转化为具体问题的解法。

4.总结
洪水灌溉系列问题的本质，是 “如何系统性地探索并处理网格中的连通区域” 。从简单的“数岛屿”到复杂的“带条件的单起点扩散”，我们走过的每一步都是对“遍历逻辑”“标记技巧”“思维角度”的深化。

未来遇到新的网格问题时，不妨先问自己：

• 起点在哪里？
• 需要向哪些方向扩散？
• 如何标记已访问区域？
• 有哪些过滤条件会影响扩散？

想清楚这四个问题，再结合洪水灌溉的基础框架，就能举一反三，轻松应对各类变体。算法学习的核心，从来不是死记代码，而是掌握“不变的逻辑”，并灵活调整“可变的细节”——这正是这一系列题目带给我们的最大收获。

欢迎在评论区分享你的解题思路或优化方案，一起碰撞思维火花～🌟

觉得有收获的话，不妨点个赞鼓励一下～顺手关注专栏，后续还有更多算法进阶内容，带你稳步提升不迷路！😉

随着洪水灌溉系列的收尾，接下来我们将进入DFS的记忆化搜索新专题——这是优化递归效率的核心技巧，能帮你解决更多“重复计算”场景的问题。下次咱们要讨论的入门题是力扣 509. 斐波那契数，看似简单的递归背后藏着记忆化的精妙逻辑，感兴趣的朋友可以提前琢磨：如何用缓存避免重复计算？递归与记忆化结合能带来多大的效率提升？蹲一波更新，带你从基础案例吃透记忆化搜索的本质～

这是封面原图～谢谢支持！