目录
1 MLP
2 LeNet简介
3 Minst数据集
3.1 MINST数据集简介
3.2 MNIST数据集的预处理
4 LeNet手写数字识别
LeNet由Yann Lecun 提出,是一种经典的卷积神经网络,是现代卷积神经网络的起源之一。Yann将该网络用于邮局的邮政的邮政编码识别,有着良好的学习和识别能力。LeNet又称LeNet-5,具有一个输入层,两个卷积层,两个池化层,3个全连接层(其中最后一个全连接层为输出层)。
1 MLP
多层感知机MLP(Multilayer Perceptron),也是人工神经网络(ANN,Artificial Neural Network),是一种全连接(全连接:MLP由多个神经元按照层次结构组成,每个神经元都与上一层的所有神经元相连)的前馈神经网络模型。
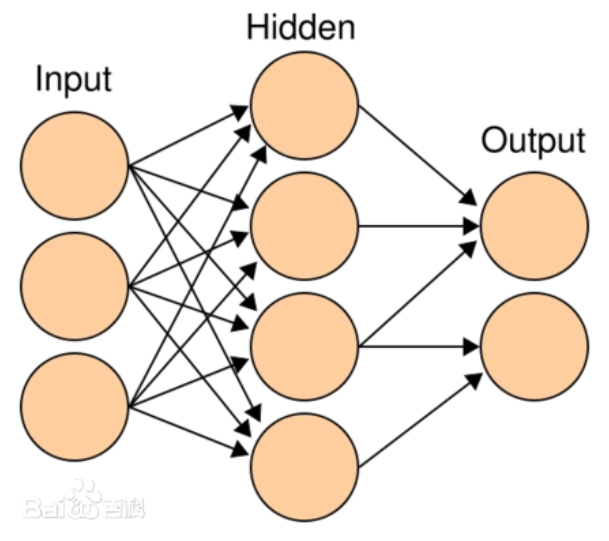
多层感知机(Multilayer Perceptron, MLP)是一种前馈神经网络,它由输入层、若干隐藏层和输出层组成。每一层都由多个神经元(或称为节点)组成。
-
输入层(Input Layer):输入层接收外部输入的数据,将其传递到下一层。每个输入特征都对应一个神经元。
-
隐藏层(Hidden Layer):隐藏层是位于输入层和输出层之间的一层或多层神经元。每个隐藏层的神经元接收上一层传来的输入,并通过权重和激活函数进行计算,然后将结果传递到下一层。隐藏层的存在可以使多层感知机具备更强的非线性拟合能力。
-
输出层(Output Layer):输出层接收隐藏层的输出,并产生最终的输出结果。输出层的神经元数目通常与任务的输出类别数目一致。对于分类任务,输出层通常使用softmax激活函数来计算每个类别的概率分布;对于回归任务,输出层可以使用线性激活函数。
多层感知机的各层之间是全连接的,也就是说,每个神经元都与上一层的每个神经元相连。每个连接都有一个与之相关的权重和一个偏置。
2 LeNet简介
LeNet-5模型是由杨立昆(Yann LeCun)教授于1998年在论文Gradient-Based Learning Applied to Document Recognition中提出的,是一种用于手写体字符识别的非常高效的卷积神经网络,其实现过程如下图所示。
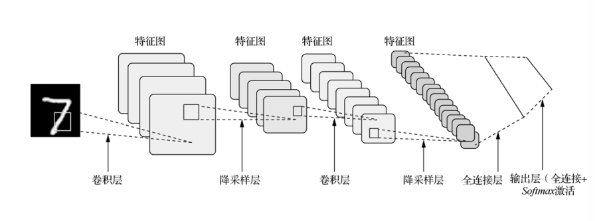
原论文的经典的LeNet-5网络结构如下:
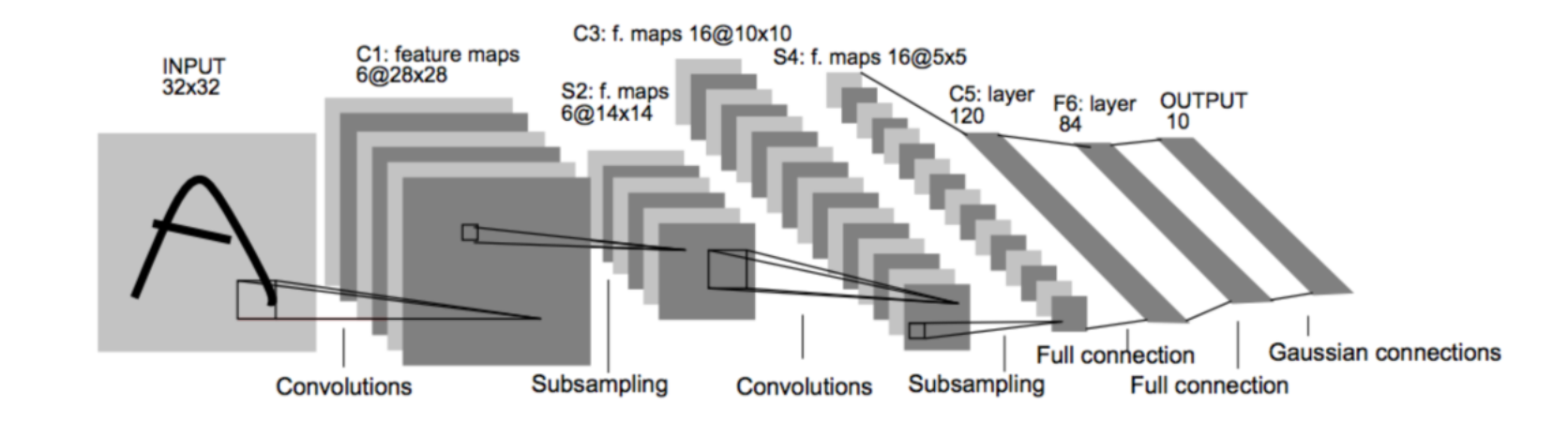
各个结构作用:
卷积层:提取特征图的特征,浅层的卷积提取的是一些纹路、轮廓等浅层的空间特征,对于深层的卷积,可以提取出深层次的空间特征。
池化层: 1、降低维度 2、最大池化或者平均池化,在本网络结构中使用的是最大池化。
全连接层: 1、输出结果 2、位置:一般位于CNN网络的末端。 3、操作:需要将特征图reshape成一维向量,再送入全连接层中进行分类或者回归。
下来我们使用代码详解推理一下各卷积层参数的变化:
import torch
import torch.nn as nn# 定义张量x,它的尺寸是1×1×28×28
# 表示了1个,单通道,32×32大小的数据
x = torch.zeros([1, 1, 32, 32])
# 定义一个输入通道是1,输出通道是6,卷积核大小是5x5的卷积层
conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
# 将x,输入至conv,计算出结果c
c1 = conv1(x)
# 打印结果尺寸程序输出:
print(c1.shape)# 定义最大池化层
pool = nn.MaxPool2d(2)
# 将卷积层计算得到的特征图c,输入至pool
s1 = pool(c1)
# 输出s的尺寸
print(s1.shape)# 定义第二个输入通道是6,输出通道是16,卷积核大小是5x5的卷积层
conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
# 将x,输入至conv,计算出结果c
c2 = conv2(s1)
# 打印结果尺寸程序输出:
print(c2.shape)s2 = pool(c2)
# 输出s的尺寸
print(s2.shape)输出结果:
torch.Size([1, 6, 28, 28])
torch.Size([1, 6, 14, 14])
torch.Size([1, 16, 10, 10])
torch.Size([1, 16, 5, 5])下面是使用pytorch实现一个最简单的LeNet模型。、
import torch
import torch.nn as nn
import torch.nn.functional as Fclass LeNet(nn.Module):def __init__(self):super(LeNet, self).__init__()# 定义卷积层self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1)self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)# 定义全连接层self.fc1 = nn.Linear(16 * 5 * 5, 120)self.fc2 = nn.Linear(120, 84)self.fc3 = nn.Linear(84, 10)# 定义激活函数self.relu = nn.ReLU()def forward(self, x):# 卷积层 + 池化层 + 激活函数x = self.relu(self.conv1(x))x = F.avg_pool2d(x, kernel_size=2, stride=2)x = self.relu(self.conv2(x))x = F.avg_pool2d(x, kernel_size=2, stride=2)# 展平特征图x = torch.flatten(x, 1)# 全连接层x = self.relu(self.fc1(x))x = self.relu(self.fc2(x))x = self.fc3(x)return x# 创建模型实例
model = LeNet()# 打印模型结构
print(model)输出结果:
LeNet((conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))(fc1): Linear(in_features=400, out_features=120, bias=True)(fc2): Linear(in_features=120, out_features=84, bias=True)(fc3): Linear(in_features=84, out_features=10, bias=True)(relu): ReLU()
)3 Minst数据集
MNIST是一个手写数字集合,该数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。
3.1 MINST数据集简介
-
该数据集包含60,000个用于训练的示例和10,000个用于测试的示例。
-
数据集包含了0-9共10类手写数字图片,每张图片都做了尺寸归一化,都是28x28大小的灰度图。
-
MNIST数据集包含四个部分: 训练集图像:train-images-idx3-ubyte.gz(9.9MB,包含60000个样本) 训练集标签:train-labels-idx1-ubyte.gz(29KB,包含60000个标签) 测试集图像:t10k-images-idx3-ubyte.gz(1.6MB,包含10000个样本) 测试集标签:t10k-labels-idx1-ubyte.gz(5KB,包含10000个标签)
3.2 MNIST数据集的预处理
这里我们可以观察训练集、验证集、测试集分别有50000,10000,10000张图片,并且读取训练集的第一张图片看看。
import torch
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import numpy as np
import struct# 图像预处理:将图像转换为 (784, 1) 的张量
transform = transforms.Compose([transforms.ToTensor(), # 转为 [0,1] 范围的 Tensortransforms.Lambda(lambda x: x.view(-1, 1)) # 展平为 (784, 1)
])# 加载 MNIST 训练集和测试集
train_dataset = datasets.MNIST(root='./dataset',train=True,transform=transform,download=True
)test_dataset = datasets.MNIST(root='./dataset',train=False,transform=transform,download=True
)# 使用 DataLoader 批量加载
train_loader = DataLoader(dataset=train_dataset,batch_size=64,shuffle=True
)test_loader = DataLoader(dataset=test_dataset,batch_size=64,shuffle=False
)# ✅ 打印训练集和测试集的样本数量
print(f"训练集样本数量: {len(train_dataset)}")
print(f"测试集样本数量: {len(test_dataset)}")# ✅ 控制台输出矩阵的代码
print("=" * 140)
print("图像矩阵的十六进制表示(非零值用红色标出):")
data = train_dataset[0][0].squeeze().numpy() # 获取第一张图像并转换为 numpy 数组
rows = 28
columns = 28counter = 0
for i in range(rows):row = data[i * columns: (i + 1) * columns]for value in row:integer_part = int(value * 100)# 防止溢出 unsigned short (0~65535)integer_part = max(0, min(65535, integer_part))hex_bytes = struct.pack('H', integer_part)hex_string = hex_bytes.hex()if hex_string == '0000':print(hex_string + ' ', end="")else:print(f'\033[31m{hex_string}\033[0m' + " ", end="")counter += 1if counter % 28 == 0:print() # 换行
print("=" * 140)# 示例:取出第一个 batch 的数据
for images, labels in train_loader:print("Batch Images Shape:", images.shape) # [batch_size, 784, 1]print("Batch Labels Shape:", labels.shape) # [batch_size]# 显示第一张图像img = images[0].reshape(28, 28).numpy()plt.imshow(img, cmap='gray')plt.title(f"Label: {labels[0].item()}")plt.axis('off')plt.show()break # 只显示一个 batch输出结果:
训练集样本数量: 60000
测试集样本数量: 100004 LeNet手写数字识别
代码实现如下:
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import time
from matplotlib import pyplot as pltpipline_train = transforms.Compose([# 随机旋转图片# MNIST 是手写数字数据集,左右翻转可能造成语义错误(例如,6 和 9 会被混淆)。所以不建议使用# transforms.RandomHorizontalFlip(),# 将图片尺寸resize到32x32transforms.Resize((32, 32)),# 将图片转化为Tensor格式transforms.ToTensor(),# 正则化(当模型出现过拟合的情况时,用来降低模型的复杂度)transforms.Normalize((0.1307,), (0.3081,))
])
pipline_test = transforms.Compose([# 将图片尺寸resize到32x32transforms.Resize((32, 32)),transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))
])
# 下载数据集
train_set = datasets.MNIST(root="./dataset", train=True, download=True, transform=pipline_train)
test_set = datasets.MNIST(root="./dataset", train=False, download=True, transform=pipline_test)
# 加载数据集
trainloader = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(test_set, batch_size=32, shuffle=False)# 构建LeNet模型
class LeNet(nn.Module):def __init__(self):super(LeNet, self).__init__()self.conv1 = nn.Conv2d(1, 6, 5)self.relu = nn.ReLU()self.maxpool1 = nn.MaxPool2d(2, 2)self.conv2 = nn.Conv2d(6, 16, 5)self.maxpool2 = nn.MaxPool2d(2, 2)self.fc1 = nn.Linear(16 * 5 * 5, 120)self.fc2 = nn.Linear(120, 84)self.fc3 = nn.Linear(84, 10)def forward(self, x):x = self.conv1(x)x = self.relu(x)x = self.maxpool1(x)x = self.conv2(x)x = self.maxpool2(x)x = x.view(-1, 16 * 5 * 5)x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return x# 创建模型,部署gpu
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = LeNet().to(device)
# 定义优化器
optimizer = optim.Adam(model.parameters(), lr=0.001)def train_runner(model, device, trainloader, optimizer, epoch):model.train()total_loss = 0total_correct = 0total_samples = 0for i, (inputs, labels) in enumerate(trainloader):inputs, labels = inputs.to(device), labels.to(device)optimizer.zero_grad()outputs = model(inputs)loss = F.cross_entropy(outputs, labels)predict = outputs.argmax(dim=1)correct = (predict == labels).sum().item()loss.backward()optimizer.step()total_loss += loss.item()total_correct += correcttotal_samples += labels.size(0)if i % 100 == 0:print(f"Epoch {epoch}, Batch {i}, Loss: {loss.item():.6f}, Accuracy: {correct / labels.size(0) * 100:.2f}%")avg_loss = total_loss / len(trainloader)avg_acc = total_correct / total_samplesprint(f"Epoch {epoch} - Average Loss: {avg_loss:.6f}, Accuracy: {avg_acc * 100:.2f}%")return avg_loss, avg_accdef test_runner(model, device, testloader):# 模型验证, 必须要写, 否则只要有输入数据, 即使不训练, 它也会改变权值# 因为调用eval()将不启用 BatchNormalization 和 Dropout, BatchNormalization和Dropout置为Falsemodel.eval()# 统计模型正确率, 设置初始值correct = 0.0test_loss = 0.0total = 0# torch.no_grad将不会计算梯度, 也不会进行反向传播with torch.no_grad():for data, label in testloader:data, label = data.to(device), label.to(device)output = model(data)test_loss += F.cross_entropy(output, label).item()predict = output.argmax(dim=1)# 计算正确数量total += label.size(0)correct += (predict == label).sum().item()# 计算损失值print("test_avarage_loss: {:.6f}, accuracy: {:.6f}%".format(test_loss / total, 100 * (correct / total)))# 调用
epoch = 5
Loss = []
Accuracy = []
for epoch in range(1, epoch + 1):print("start_time", time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(time.time())))loss, acc = train_runner(model, device, trainloader, optimizer, epoch)Loss.append(loss)Accuracy.append(acc)test_runner(model, device, testloader)print("end_time: ", time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(time.time())), '\n')print('Finished Training')plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(Loss)
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')plt.subplot(1, 2, 2)
plt.plot(Accuracy)
plt.title('Training Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.tight_layout()
plt.show()输出效果:
start_time 2025-07-21 23:55:06
Epoch 1, Batch 0, Loss: 2.289716, Accuracy: 10.94%
Epoch 1, Batch 100, Loss: 0.193995, Accuracy: 96.88%
Epoch 1, Batch 200, Loss: 0.182066, Accuracy: 93.75%
Epoch 1, Batch 300, Loss: 0.188292, Accuracy: 95.31%
Epoch 1, Batch 400, Loss: 0.124157, Accuracy: 95.31%
Epoch 1, Batch 500, Loss: 0.034723, Accuracy: 100.00%
Epoch 1, Batch 600, Loss: 0.008845, Accuracy: 100.00%
Epoch 1, Batch 700, Loss: 0.085703, Accuracy: 98.44%
Epoch 1, Batch 800, Loss: 0.043274, Accuracy: 100.00%
Epoch 1, Batch 900, Loss: 0.081251, Accuracy: 96.88%
Epoch 1 - Average Loss: 0.204190, Accuracy: 93.77%
test_avarage_loss: 0.001810, accuracy: 98.210000%
end_time: 2025-07-21 23:55:36 start_time 2025-07-21 23:55:36
Epoch 2, Batch 0, Loss: 0.007833, Accuracy: 100.00%
Epoch 2, Batch 100, Loss: 0.026923, Accuracy: 98.44%
Epoch 2, Batch 200, Loss: 0.055813, Accuracy: 98.44%
Epoch 2, Batch 300, Loss: 0.021718, Accuracy: 98.44%
Epoch 2, Batch 400, Loss: 0.044155, Accuracy: 98.44%
Epoch 2, Batch 500, Loss: 0.078634, Accuracy: 98.44%
Epoch 2, Batch 600, Loss: 0.077378, Accuracy: 98.44%
Epoch 2, Batch 700, Loss: 0.024615, Accuracy: 98.44%
Epoch 2, Batch 800, Loss: 0.065229, Accuracy: 95.31%
Epoch 2, Batch 900, Loss: 0.105533, Accuracy: 96.88%
Epoch 2 - Average Loss: 0.058598, Accuracy: 98.17%
test_avarage_loss: 0.001409, accuracy: 98.510000%
end_time: 2025-07-21 23:56:09 start_time 2025-07-21 23:56:09
Epoch 3, Batch 0, Loss: 0.008086, Accuracy: 100.00%
Epoch 3, Batch 100, Loss: 0.007276, Accuracy: 100.00%
Epoch 3, Batch 200, Loss: 0.026653, Accuracy: 98.44%
Epoch 3, Batch 300, Loss: 0.013348, Accuracy: 100.00%
Epoch 3, Batch 400, Loss: 0.051161, Accuracy: 98.44%
Epoch 3, Batch 500, Loss: 0.011193, Accuracy: 100.00%
Epoch 3, Batch 600, Loss: 0.018030, Accuracy: 100.00%
Epoch 3, Batch 700, Loss: 0.031486, Accuracy: 98.44%
Epoch 3, Batch 800, Loss: 0.040127, Accuracy: 96.88%
Epoch 3, Batch 900, Loss: 0.003004, Accuracy: 100.00%
Epoch 3 - Average Loss: 0.041799, Accuracy: 98.73%
test_avarage_loss: 0.001054, accuracy: 98.890000%
end_time: 2025-07-21 23:56:42 start_time 2025-07-21 23:56:42
Epoch 4, Batch 0, Loss: 0.005576, Accuracy: 100.00%
Epoch 4, Batch 100, Loss: 0.004955, Accuracy: 100.00%
Epoch 4, Batch 200, Loss: 0.025697, Accuracy: 98.44%
Epoch 4, Batch 300, Loss: 0.060617, Accuracy: 98.44%
Epoch 4, Batch 400, Loss: 0.011967, Accuracy: 100.00%
Epoch 4, Batch 500, Loss: 0.006767, Accuracy: 100.00%
Epoch 4, Batch 600, Loss: 0.060184, Accuracy: 98.44%
Epoch 4, Batch 700, Loss: 0.018019, Accuracy: 98.44%
Epoch 4, Batch 800, Loss: 0.052307, Accuracy: 98.44%
Epoch 4, Batch 900, Loss: 0.002293, Accuracy: 100.00%
Epoch 4 - Average Loss: 0.033747, Accuracy: 98.92%
test_avarage_loss: 0.001589, accuracy: 98.420000%
end_time: 2025-07-21 23:57:15 start_time 2025-07-21 23:57:15
Epoch 5, Batch 0, Loss: 0.028971, Accuracy: 98.44%
Epoch 5, Batch 100, Loss: 0.002826, Accuracy: 100.00%
Epoch 5, Batch 200, Loss: 0.001654, Accuracy: 100.00%
Epoch 5, Batch 300, Loss: 0.021051, Accuracy: 100.00%
Epoch 5, Batch 400, Loss: 0.122267, Accuracy: 95.31%
Epoch 5, Batch 500, Loss: 0.011313, Accuracy: 100.00%
Epoch 5, Batch 600, Loss: 0.007512, Accuracy: 100.00%
Epoch 5, Batch 700, Loss: 0.029513, Accuracy: 98.44%
Epoch 5, Batch 800, Loss: 0.006132, Accuracy: 100.00%
Epoch 5, Batch 900, Loss: 0.015854, Accuracy: 98.44%
Epoch 5 - Average Loss: 0.027342, Accuracy: 99.14%
test_avarage_loss: 0.001210, accuracy: 98.840000%
end_time: 2025-07-21 23:57:47 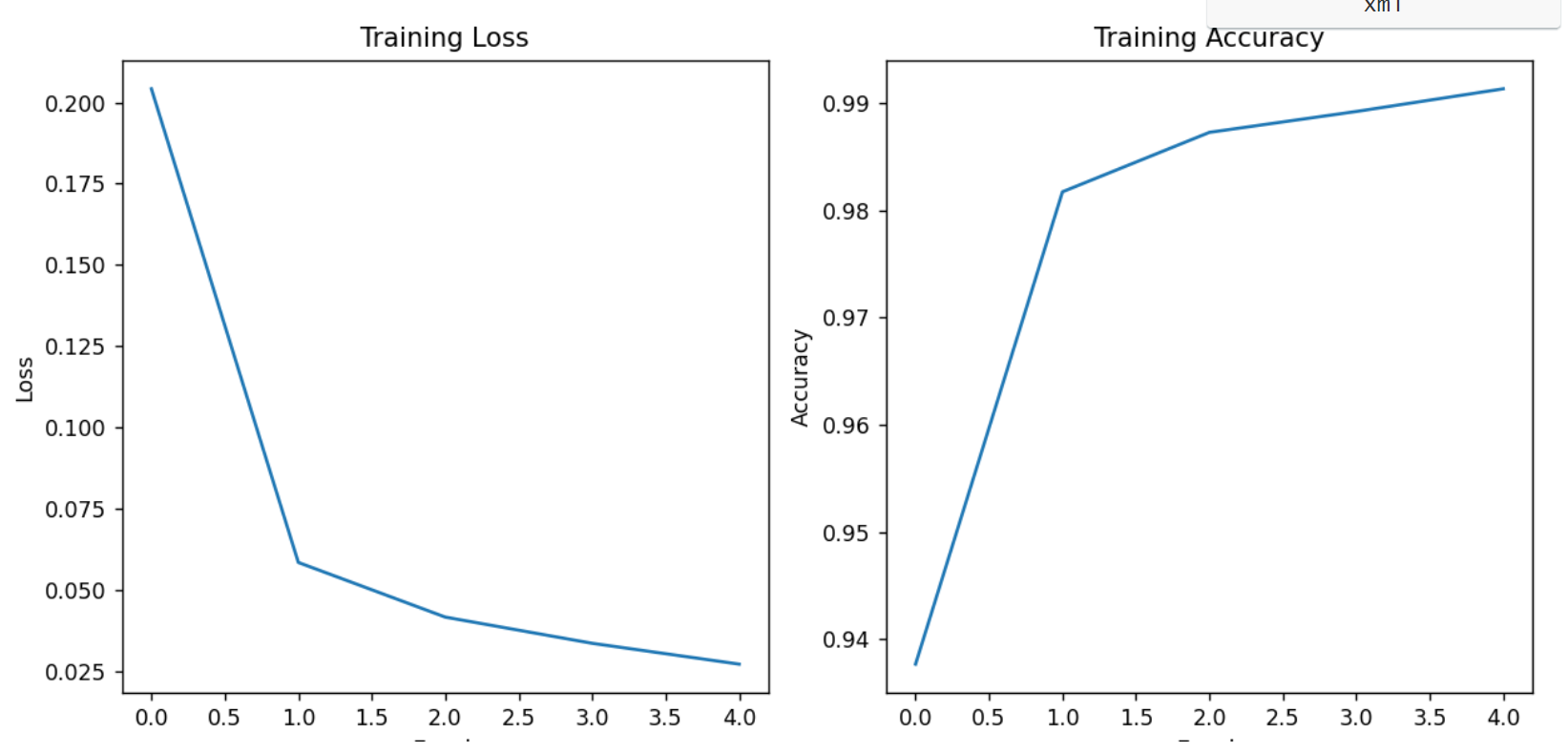
增加模型预测功能:
model.load_state_dict(torch.load('./mymodel.pt'))
print("成功加载模型....")index = random.randint(0,100)
image, label = train_set[index] # 从 test_set 中直接获取图像和标签
image = image.unsqueeze(0).to(device)# 进行预测
model.eval()
with torch.no_grad():output = model(image)predicted_label = output.argmax(dim=1, keepdim=True)print("Predicted label:", predicted_label[0].item())
print("Actual label:", label)运行效果:
成功加载模型....Predicted label: 9
Actual label: 9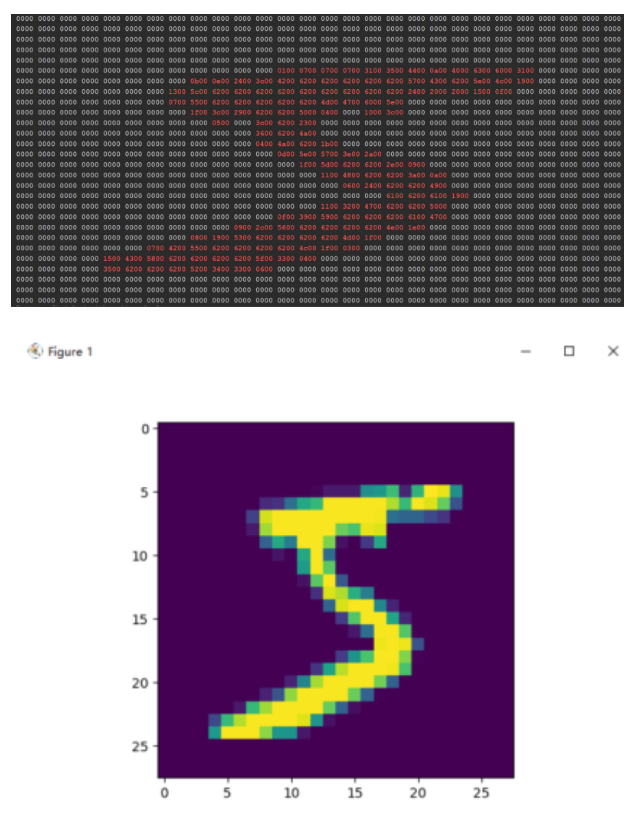




)














事件系统)