【数据结构】二叉树的链式结构--用C语言实现

1.二叉树的链式结构

此前，我们通过数组（顺序表）完成了二叉树的顺序存储，并实现了二叉树的基础功能
那么，二叉树还有没有其他存储方式呢？

前面我们学习了链表，它是一种线性结构，而二叉树是一种非线性结构，但是通过思考，我们发现链表是通过next指针把一个一个的节点连接起来的，那么我们如何用相似的方式把二叉树相应的节点连接起来呢？

//链表节点
typedef int LTDataType;//存储的数据类型
typedef struct ListNode{LTDataType val;//数据值struct ListNode* next;//指向下一个节点
}LTNOde;

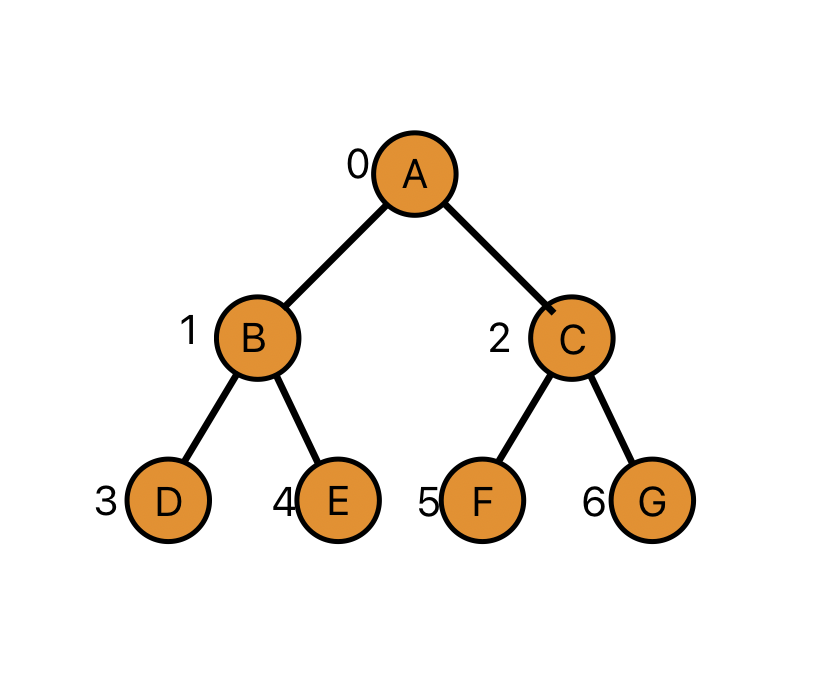
请添加图片描述

通过观察，我们发现二叉树中，节点最大的度为2(每个节点最多连接两个字节点)，所以我们可以在链表节点的基础上，再添加一个指针，用两个指针来指向子节点，即可把整个二叉树连接起来，形成一个链式结构

typedef int BTDataType;//存储的数据类型
typedef struct BinaryTreeNode{LTDataType val;//数据值//指向左子节点struct BinaryTreeNode* left;//指向右子节点struct BinaryTreeNode* right;
}BTNode;

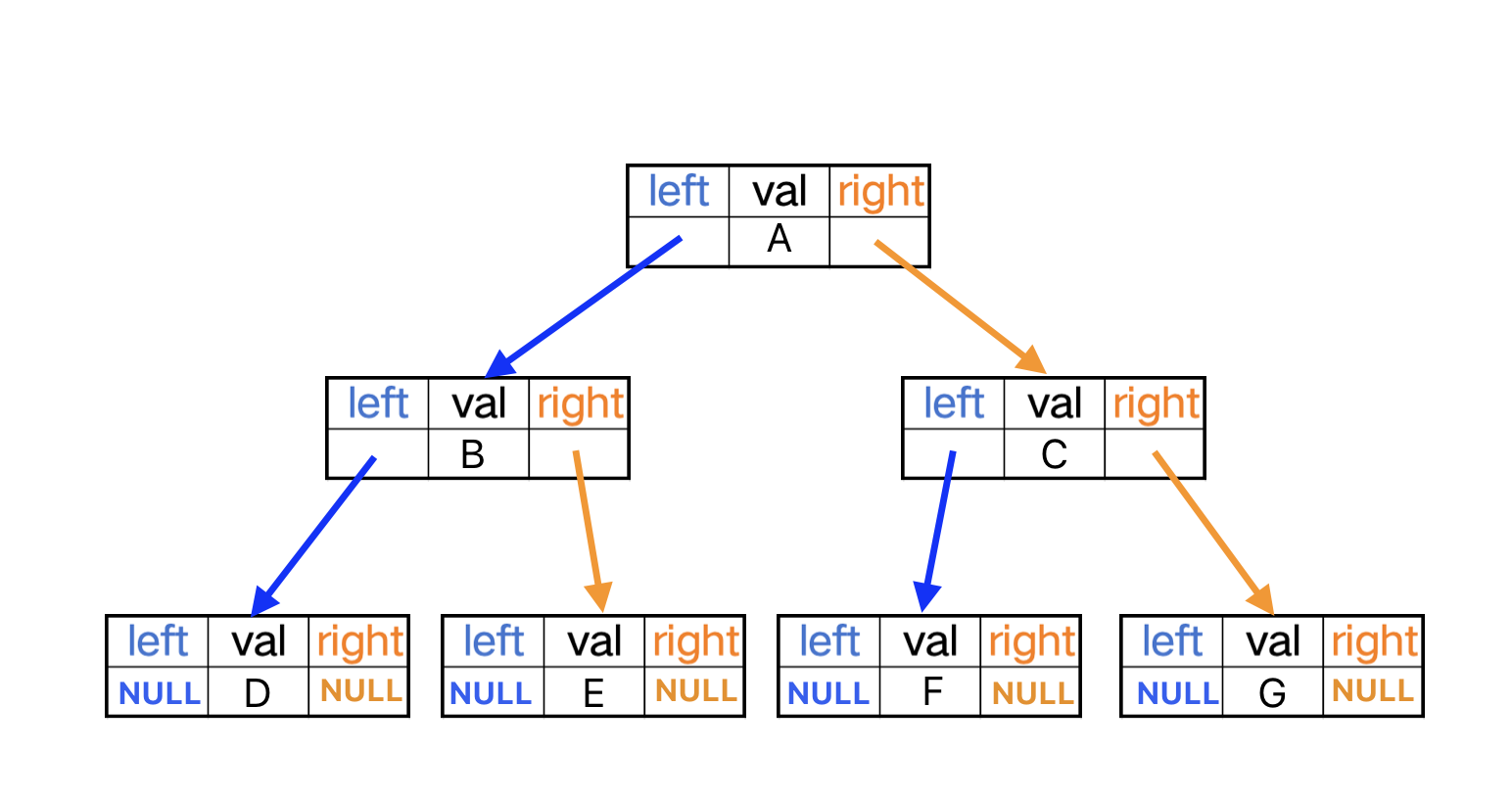
请添加图片描述

2.链式结构的遍历顺序

链式结构的遍历顺序分为三种：前序遍历、中序遍历、后序遍历

注：他们的顺序都是相对于根节点的
前序遍历：根节点-左节点-右节点
中序遍历：左节点-根节点-右节点
后续遍历：左节点-右节点-根节点

2.1.前序遍历

从根节点开始遍历，然后遍历左子树，最后遍历右子树
请添加图片描述

  1. 根节点为A(当前前序遍历结果：A)
  2. 再遍历A的左子树，继续以根-左-右的顺序遍历，找到子树的根节点B(当前前序遍历结果：A-B)
  3. 遍历B的左子树，找到D，D没有子树了，所以B的左子树遍历完了(当前前序遍历结果：A-B-D)
  4. B的根和左子树遍历完了，开始遍历B的右子树，找到节点E，此时A的左子树遍历完了(当前前序遍历结果：A-B-D-E)
  5. A的根和左子树遍历完了，开始遍历A的右子树
  6. 找到A的子树的根节点C(当前前序遍历结果：A-B-D-E-C)
  7. 开始遍历C的左子树，找到F，C的左子树遍历完毕(当前前序遍历结果：A-B-D-E-C-F)
  8. 开始遍历C的右子树，找到G，此时A的右子树遍历完毕(当前前序遍历结果：A-B-D-E-C-F-G)
  9. 前序遍历完成
  10. 最终结果为A-B-D-E-C-F-G

2.1.中序遍历

从左子树开始遍历，再遍历根节点，最后遍历右子树
请添加图片描述
11. 先遍历根节点A的左子树，来到子树中的根节点B，他有左子树，继续向下遍历找他的左子树，找到节点D，由于D没有左子树了，所以取D(当前中序遍历结果：D-)
12. B的左子树遍历完了，遍历根B本身，取B(当前中序遍历结果：D-😎
13. 遍历B的右子树，找到E，E没有子树了，取E，B的右子树遍历完成(当前中序遍历结果：D-B-E)
14. 此时A的左子树遍历完成，遍历根A本身，取A(当前中序遍历结果：D-B-E-A)
15. A的左子树和根遍历完成，遍历A的右子树来到C，C有左子树，来到F，F没有子树了，取F(当前中序遍历结果：D-B-E-A-F)
16. C的左子树遍历完成，遍历根C本身，取节点C(当前中序遍历结果：D-B-E-A-F-C)
17. C的左子树和根遍历完成，遍历右子树，找到节点G，它没有子树了，取G(当前中序遍历结果：D-B-E-A-F-C-G)
18. A的右子树遍历完成，中序遍历完毕
19. 最终结果为D-B-E-A-F-C-G

2.3.后序遍历

从左子树开始遍历，再遍历右子树，最后遍历根
请添加图片描述

  1. 先遍历根A的左子树，找到节点B，B有左子树，继续遍历，找到节点D，D没有子树了，取D(当前后序遍历结果：D)
  2. B的左子树遍历完成，继续遍历它的右子树，找到节点E，没有子树了，取E(当前后序遍历结果：D-E)
  3. B的右子树遍历完成，取B本身(当前后序遍历结果：D-E-B)
  4. A的左子树遍历完成，继续遍历A的右子树，找到节点C，继续遍历C的左子树，找到节点F，F没有子树了，取F(当前后序遍历结果：D-E-B-F)
  5. C的左子树遍历完成，继续遍历它的右子树，找到节点G，G没有子树了，取G(当前后序遍历结果：D-E-B-F-G)
  6. C的左右子树遍历完成，取根C本身(当前后序遍历结果：D-E-B-F-G-C)
  7. 此时A的左右子树遍历完成，取根A本身(当前后序遍历结果：D-E-B-F-G-C-A)
  8. 后序遍历完成，最终结果为D-E-B-F-G-C-A

3.二叉树链式结构的实现

3.1.二叉树节点结构的定义

一个结构体类型，成员包含存储数据的值和分别指向左孩子和右孩子的左右指针

typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

3.2.创建节点

开辟一个节点大小的空间，把数据值存入该节点，返回这片空间的地址

BTNode* BTBuyNode(BTDataType x)
{BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));if(newNode == NULL){perror("malloc error!\n");return NULL;}newNode->_data = x;newNode->_left = newNode->_right = NULL;return newNode;
}

3.3.创建二叉树

以前序遍历为例，把数组中的数据，转化为链式结构，存储到二叉树中

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if(*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BTBuyNode(a[(*pi)++]);root->_left = BinaryTreeCreate(a, n, pi);root->_right = BinaryTreeCreate(a, n, pi);return root;
}

注：形参中的pi必须传指针(传址调用)，因为在递归过程中该形参会发生改变，如果采用传值调用，该形参值不能被正常修改

3.4.二叉树链式结构的销毁

以后序遍历的方式，先销毁左右子树，最后销毁根节点（如果先销毁根节点，那就找不到它的左右指针了，不能进行后续操作）

//左-右-根
void BinaryTreeDestory(BTNode** root)
{if(root == NULL || *root == NULL){return ;}//注：传二级指针--指针的地址BinaryTreeDestory(&((*root)->_left));BinaryTreeDestory(&((*root)->_right));free(*root);*root = NULL;
}

3.5.节点总数

用递归的方式，返回左子树的节点个数+右子树的节点个数+根即可

int BinaryTreeSize(BTNode* root)
{if(root == NULL) return 0;return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
}

3.6.叶子节点数

同样用递归的方式，返回左子树的叶子节点数+右子树的叶子节点数，当该节点没有左右子树时，即为叶子节点，返回1

int BinaryTreeLeafSize(BTNode* root)
{if(root == NULL) return 0;if(!root->_left && !root->_right) return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

3.7.返回第K层的节点数

同样采用递归的方式，第K层节点数=根节点左子树的第K-1层节点数+根节点的右子树的第K-1层节点数，以此类推，每递归一次都减少一层···

int BinaryTreeLevelKSize(BTNode* root, int k)
{if(root == NULL || k < 1) return 0;if(k == 1) return 1;return BinaryTreeLevelKSize(root->_left, k-1) + BinaryTreeLevelKSize(root->_right, k-1);
}

3.8.查找节点

还是采用递归的方式，从根节点开始，遍历每一个节点，直到遇到目标值，返回该节点的地址

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if(root == NULL) return NULL;if(root->_data == x) return root;BTNode* Left = BinaryTreeFind(root->_left, x);BTNode* Right = BinaryTreeFind(root->_right, x);if(Left) return Left;if(Right) return Right;return NULL;
}

3.9.前序遍历

先打印根节点数据，再分别递归调用左子树和右子树

//根-左-右
void BinaryTreePrevOrder(BTNode* root)
{if(root == NULL) return;printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

3.10.中序遍历

先递归调用左子树，再打印根节点数据，最后递归调用右子树

//左-根-右
void BinaryTreeInOrder(BTNode* root)
{if(root == NULL) return;BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}

3.11.后序遍历

先分别递归调用左右子树，再打印根节点

//左-右-根
void BinaryTreePostOrder(BTNode* root)
{if(root == NULL) return;BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}

3.12.层序遍历

由于每一个节点都是通过指针连接的后继节点，所以一层一层地调用是不现实的，这个时候我们可以借助队列来实现层序遍历：

创建一个队列，先让根节点入队，取出队列头节点并打印，（如果有的话）让它的左右孩子入队，若队列不为空，继续取出队头节点并打印，让它的左右孩子入队，重复以上操作，直到队列为空，则层序遍历完成

队列的实现（队列的详细讲解）：
Queue.h

//
//  Queue.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef struct BinaryTreeNode BTNode;
//队列节点的结构
typedef struct QueueNode{BTNode* data;struct QueueNode* next;
}QueueNode;
//队列的结构
typedef struct Queue{QueueNode* front;QueueNode* rear;
}Queue;//初始化队列
void QueueInit(Queue* pq);//入队
void QueuePush(Queue* pq, BTNode* x);//判空
bool QueueEmpty(Queue* pq);//出队
void QueuePop(Queue* pq);//取队头
BTNode* QueueFront(Queue* pq);//销毁队列
void QueueDestroy(Queue* pq);

Queue.c

//
//  Queue.c
#include "Queue.h"
void QueueInit(Queue* pq)
{assert(pq);pq->front = pq->rear = NULL;
}void QueuePush(Queue* pq, BTNode* x)
{assert(pq);QueueNode* newQueNode = (QueueNode*)malloc(sizeof(QueueNode));if(newQueNode == NULL){perror("malloc fail!\n");return;}newQueNode->data = x;newQueNode->next = NULL;if(pq->front == NULL){pq->front = pq->rear = newQueNode;}else{pq->rear->next = newQueNode;pq->rear = newQueNode;}
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->front == NULL;
}void QueuePop(Queue* pq)
{assert(!QueueEmpty(pq));QueueNode* del = pq->front;pq->front = del->next;if(pq->front == NULL){pq->rear = NULL;}free(del);del = NULL;
}BTNode* QueueFront(Queue* pq)
{assert(!QueueEmpty(pq));return pq->front->data;
}
void QueueDestroy(Queue* pq)
{//节点QueueNode* pcur = pq->front;while(pcur){QueueNode* next= pcur->next;free(pcur);pcur = next;}//队列首尾pq->front = pq->rear = NULL;
}

层序遍历：

void BinaryTreeLevelOrder(BTNode* root)
{if(root == NULL) return;Queue q;QueueInit(&q);QueuePush(&q, root);while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->_data);if(top->_left) QueuePush(&q, top->_left);if(top->_right) QueuePush(&q, top->_right);}QueueDestroy(&q);
}

3.13.判断是否为完全二叉树

我们知道，完全二叉树是由满二叉树得来的，在完全二叉树中，最后一层以上的所有层次中，节点数都达到了最大值，而最后一层不一定，但一定满足节点从左到右依次排列
因此，我们可以通过此性质，仿照层次遍历的方式，通过队列，来实现完全二叉树的判定
注：取队头时，不需要判断左右孩子是否为空，直接入队即可，当队列头节点为空时，跳出循环，此时判断队列后序数据是否存在非空值，若存在，则不是完全二叉树，不存在，则是完全二叉树

bool BinaryTreeComplete(BTNode* root)
{//当遍历到空节点时 递归结束if(root == NULL) return true;Queue q;QueueInit(&q);while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);//判断是否为空节点if(top == NULL){break;}//左右子树入队QueuePush(&q, top->_left);QueuePush(&q, top->_right);}//检查剩余元素while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);//判断队头元素if(top != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

4.完整代码

Queue.h

//
//  Queue.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef struct BinaryTreeNode BTNode;
//队列节点的结构
typedef struct QueueNode{BTNode* data;struct QueueNode* next;
}QueueNode;
//队列的结构
typedef struct Queue{QueueNode* front;QueueNode* rear;
}Queue;//初始化队列
void QueueInit(Queue* pq);//入队
void QueuePush(Queue* pq, BTNode* x);//判空
bool QueueEmpty(Queue* pq);//出队
void QueuePop(Queue* pq);//取队头
BTNode* QueueFront(Queue* pq);//销毁队列
void QueueDestroy(Queue* pq);

Tree.h

//
//  Tree.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <string.h>typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;//创建节点
BTNode* BTBuyNode(BTDataType x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);

Queue.c

//
//  Queue.c
#include "Queue.h"
void QueueInit(Queue* pq)
{assert(pq);pq->front = pq->rear = NULL;
}void QueuePush(Queue* pq, BTNode* x)
{assert(pq);QueueNode* newQueNode = (QueueNode*)malloc(sizeof(QueueNode));if(newQueNode == NULL){perror("malloc fail!\n");return;}newQueNode->data = x;newQueNode->next = NULL;if(pq->front == NULL){pq->front = pq->rear = newQueNode;}else{pq->rear->next = newQueNode;pq->rear = newQueNode;}
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->front == NULL;
}void QueuePop(Queue* pq)
{assert(!QueueEmpty(pq));QueueNode* del = pq->front;pq->front = del->next;if(pq->front == NULL){pq->rear = NULL;}free(del);del = NULL;
}BTNode* QueueFront(Queue* pq)
{assert(!QueueEmpty(pq));return pq->front->data;
}
void QueueDestroy(Queue* pq)
{//节点QueueNode* pcur = pq->front;while(pcur){QueueNode* next= pcur->next;free(pcur);pcur = next;}//队列首尾pq->front = pq->rear = NULL;
}

Tree.c

//
//  Tree.c
#include "Tree.h"
#include "Queue.h"BTNode* BTBuyNode(BTDataType x)
{BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));if(newNode == NULL){perror("malloc error!\n");return NULL;}newNode->_data = x;newNode->_left = newNode->_right = NULL;return newNode;
}
//前序：根-左-右
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if(*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BTBuyNode(a[(*pi)++]);root->_left = BinaryTreeCreate(a, n, pi);root->_right = BinaryTreeCreate(a, n, pi);return root;
}//左-右-根
void BinaryTreeDestory(BTNode** root)
{if(root == NULL || *root == NULL){return ;}BinaryTreeDestory(&((*root)->_left));BinaryTreeDestory(&((*root)->_right));free(*root);*root = NULL;
}int BinaryTreeSize(BTNode* root)
{if(root == NULL) return 0;return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
}int BinaryTreeLeafSize(BTNode* root)
{if(root == NULL) return 0;if(!root->_left && !root->_right) return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}int BinaryTreeLevelKSize(BTNode* root, int k)
{if(root == NULL || k < 1) return 0;if(k == 1) return 1;return BinaryTreeLevelKSize(root->_left, k-1) + BinaryTreeLevelKSize(root->_right, k-1);
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if(root == NULL) return NULL;if(root->_data == x) return root;BTNode* Left = BinaryTreeFind(root->_left, x);BTNode* Right = BinaryTreeFind(root->_right, x);if(Left) return Left;if(Right) return Right;return NULL;
}//根-左-右
void BinaryTreePrevOrder(BTNode* root)
{if(root == NULL) return;printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
//左-根-右
void BinaryTreeInOrder(BTNode* root)
{if(root == NULL) return;BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}
//左-右-根
void BinaryTreePostOrder(BTNode* root)
{if(root == NULL) return;BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}
//借助队列来实现
void BinaryTreeLevelOrder(BTNode* root)
{if(root == NULL) return;Queue q;QueueInit(&q);QueuePush(&q, root);while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->_data);if(top->_left) QueuePush(&q, top->_left);if(top->_right) QueuePush(&q, top->_right);}QueueDestroy(&q);
}bool BinaryTreeComplete(BTNode* root)
{if(root == NULL) return true;Queue q;QueueInit(&q);while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);if(top == NULL){break;}QueuePush(&q, top->_left);QueuePush(&q, top->_right);}while(!QueueEmpty(&q)){BTNode* top =QueueFront(&q);QueuePop(&q);if(top != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

main.c

//
//  main.c#include "Tree.h"
void test(void)
{char str[] = "ABD##E#H##CF##G##";int i = 0;int n = (int)strlen(str);BTNode* root = BinaryTreeCreate(str, n, &i);printf("二叉树节点总数为：%d\n", BinaryTreeSize(root));printf("二叉树叶子结点数为：%d\n", BinaryTreeLeafSize(root));printf("二叉树第2层节点数为：%d\n", BinaryTreeLevelKSize(root, 2));printf("节点‘F’所在地址为：%p\n", BinaryTreeFind(root, 'F'));printf("二叉树前序遍历结果为：");BinaryTreePrevOrder(root);printf("\n");printf("二叉树中序遍历结果为：");BinaryTreeInOrder(root);printf("\n");printf("二叉树后序遍历结果为：");BinaryTreePostOrder(root);printf("\n");printf("二叉树层序遍历结果为：");BinaryTreeLevelOrder(root);printf("\n");BinaryTreeDestory(&root);
}
int main(void)
{test();return 0;
}

运行结果

请添加图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/web/90261.shtml
繁体地址，请注明出处：http://hk.pswp.cn/web/90261.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

java设计模式 -【适配器模式】

java设计模式 -【适配器模式】

适配器模式的定义 适配器模式&#xff08;Adapter Pattern&#xff09;是一种结构型设计模式&#xff0c;用于解决接口不兼容问题。通过将一个类的接口转换成客户端期望的另一个接口&#xff0c;使原本因接口不匹配而无法工作的类能够协同工作。 核心角色 目标接口&#xff08;…
阅读更多...
前端，demo操作，增删改查，to do list小项目

前端，demo操作，增删改查，to do list小项目

demo操作&#xff0c;html<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title>&l…
阅读更多...
Spring AI 项目实战（十九）：Spring Boot + AI + Vue3 + OSS + DashScope 构建多模态视觉理解平台（附完整源码）

Spring AI 项目实战（十九）：Spring Boot + AI + Vue3 + OSS + DashScope 构建多模态视觉理解平台（附完整源码）

系列文章 序号 文章名称 1 Spring AI 项目实战（一）：Spring AI 核心模块入门 2 Spring AI 项目实战（二）：Spring Boot + AI + DeepSeek 深度实战（附完整源码） 3 Spring AI 项目实战（三）：Spring Boot + AI + DeepSeek 打造智能客服系统（附完整源码） 4
阅读更多...
在 Ubuntu 20.04.5 LTS 系统上安装 Docker CE 26.1.4 完整指南

在 Ubuntu 20.04.5 LTS 系统上安装 Docker CE 26.1.4 完整指南

在 Ubuntu 20.04.5 LTS 系统上安装 Docker CE 26.1.4 完整指南版本选择说明 为什么选择 Docker CE 26.1.4&#xff1f; 1. 版本稳定性和成熟度 Docker CE 26.1.4 是 2024 年 5 月发布的稳定版本&#xff0c;经过了充分的测试和验证相比最新的 28.x 版本&#xff0c;26.1.4 在生…
阅读更多...
避坑指南：Windows 11中 Docker 数据卷的存放位置

避坑指南：Windows 11中 Docker 数据卷的存放位置

在 PowerShell 中使用 docker volume inspect 命令&#xff0c;输出如下&#xff1a; [{"CreatedAt": "2025-07-23T01:00:45Z","Driver": "local","Labels": null,"Mountpoint": "/var/lib/docker/volumes/…
阅读更多...
Hadoop大数据集群架构全解析

Hadoop大数据集群架构全解析

技术概述Hadoop的定义及其在大数据领域的地位Hadoop是由Apache基金会开发的开源分布式计算框架&#xff0c;基于Google的MapReduce和GFS论文思想实现&#xff0c;已成为大数据处理的事实标准。它通过分布式存储和计算解决了传统数据库无法处理的海量数据存储和分析问题&#xf…
阅读更多...
【自动化测试】Selenium Python UI自动化测试实用教程

【自动化测试】Selenium Python UI自动化测试实用教程

一、引言：Selenium与UI自动化测试基础 1.1 Selenium简介 Selenium是一个开源的Web应用自动化测试框架，支持多浏览器（Chrome、Firefox、Edge等）和多编程语言（Python、Java、JavaScript等），核心组件包括： WebDriver：通过浏览器原生API控制浏览器，模拟用户操作（点击、…
阅读更多...
基于VSCode的nRF52840开发环境搭建

基于VSCode的nRF52840开发环境搭建

nRF52840是Nordic Semiconductor推出的一款功能强大的多协议SoC&#xff0c;广泛应用于物联网设备、可穿戴设备和低功耗蓝牙产品开发。本篇文章将详细介绍如何在VSCode中搭建完整的nRF52840开发环境&#xff0c;让您能够高效地进行嵌入式开发。 一、准备工作 VSCode&#xff1a…
阅读更多...
GStreamer开发笔记（九）：gst-rtcp-server安装和部署实现简单的rtsp-server服务器推流Demo

GStreamer开发笔记（九）：gst-rtcp-server安装和部署实现简单的rtsp-server服务器推流Demo

若该文为原创文章&#xff0c;转载请注明原文出处 本文章博客地址&#xff1a;https://blog.csdn.net/qq21497936/article/details/149054288 长沙红胖子Qt&#xff08;长沙创微智科&#xff09;博文大全&#xff1a;开发技术集合&#xff08;包含Qt实用技术、树莓派、三维、O…
阅读更多...
C++ namespace机制以及同时使用多个namespace可能存在的问题

C++ namespace机制以及同时使用多个namespace可能存在的问题

在一个 .cpp 文件中使用了多个 using namespace 会怎么样&#xff1f; 核心答案是&#xff1a;可能会导致“命名冲突&#xff08;Name Collision&#xff09;”和“二义性&#xff08;Ambiguity&#xff09;”&#xff0c;从而引发编译错误。 当你使用 using namespace SomeNam…
阅读更多...
基于R语言的分位数回归技术应用

基于R语言的分位数回归技术应用

回归是科研中最常见的统计学研究方法之一&#xff0c;在研究变量间关系方面有着极其广泛的应用。由于其基本假设的限制&#xff0c;包括线性回归及广义线性回归在内的各种常见的回归方法都有三个重大缺陷&#xff1a;(1)对于异常值非常敏感&#xff0c;极少量的异常值可能导致结…
阅读更多...
网络I/O模型详解-一次了解全部(面试经常会问到相关知识)

网络I/O模型详解-一次了解全部(面试经常会问到相关知识)

前言 网络I/O模型的五种类型&#xff0c;其实在我们开发程序、设计程序、实现程序的方方面面都一直存在着&#xff0c;本文从实现原理、使用场景、优缺点、详细的流程图等方面进行深入的解释&#xff0c;帮助大家更好的理解常用的五种网络io模型&#xff0c;助力大家在工作、面…
阅读更多...
面试150 合并K个升序链表

面试150 合并K个升序链表

思路 对链表元素进行获取&#xff0c;然后进行sort()排序&#xff0c;最后通过空节点建立链表法重新建立一个有序的链表&#xff0c;返回头节点即可。 # Definition for singly-linked list. # class ListNode: # def __init__(self, val0, nextNone): # self.val …
阅读更多...
BitDistiller：通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力

BitDistiller：通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力

温馨提示&#xff1a; 本篇文章已同步至"AI专题精讲" BitDistiller&#xff1a;通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力 摘要 大语言模型&#xff08;LLMs&#xff09;的规模不断扩大&#xff0c;在自然语言处理方面取得了令人瞩目的进展&#xff0c;但这也带来…
阅读更多...
JavaScript 的 `querySelector` 方法详解

JavaScript 的 `querySelector` 方法详解

querySelector 是 JavaScript 中用于选择 DOM 元素的最强大方法之一&#xff0c;它允许你使用 CSS 选择器语法来查找元素。 基本语法 // 返回文档中第一个匹配指定 CSS 选择器的元素 element document.querySelector(selectors);// 从指定元素后代中查找 element parentEle…
阅读更多...
第九讲：C++中的list与forward_list

第九讲：C++中的list与forward_list

目录 1、list的介绍及使用 1.1、构造及赋值重载 1.2、迭代器 1.3、空间 1.4、访问 1.5、修改 1.6、操作 2、迭代器失效 3、list的模拟实现 4、forward_list介绍与使用 4.1、构造及赋值重载 4.2、迭代器 4.3、容量 4.4、访问 4.5、修改 4.6、操作 5、迭代器的分…
阅读更多...
华为云数据库 GaussDB的 nvarchar2隐式类型转换的坑

华为云数据库 GaussDB的 nvarchar2隐式类型转换的坑

bigint 与 nvarchar2比较时发生隐式类型转换的坑 1. 案例分析 假设&#xff1a; table1有下面两个字段&#xff1a;id:bigint&#xff0c; source_id nvarchar2(50)数据库中id 的值一定大于 int4 的最大值&#xff0c;例如存在一条单据&#xff1a; id1947854462980792321&…
阅读更多...
spring boot 集成netty，及其一些基本概念

spring boot 集成netty，及其一些基本概念

一、基本概念 1、channel:通道&#xff0c;入站或者出站数据的载体 2、ChannelHandler&#xff1a;通道处理器&#xff0c;业务逻辑写在这里面&#xff0c;netty 5版本将入战和出站合并成了ChannelHandler 3、ChannelPipeline&#xff1a;通道里的管道&#xff0c;是一个或者多…
阅读更多...
7月23日华为机考真题第一题100分

7月23日华为机考真题第一题100分

📌 点击直达笔试专栏 👉《大厂笔试突围》 💻 春秋招笔试突围在线OJ 👉 bishipass.com 01. 创业投资收益优化 问题描述 K小姐刚刚大学毕业，手头有 m m m 元资金想要进行创业投资。她发现了 k k
阅读更多...
HTML5 跨文档通信机制：postMessage API 详解与应用

HTML5 跨文档通信机制：postMessage API 详解与应用

postMessage 是 HTML5 规范中定义的跨文档通信&#xff08;Cross-Document Messaging&#xff09;API&#xff0c;其设计目的是解决不同源&#xff08;协议、域名、端口任一存在差异&#xff09;的窗口&#xff08;如 iframe 嵌入的文档、window.open 创建的新窗口&#xff09;…
阅读更多...
最新文章

Copyright @ 2022~2023