C++算法竞赛篇(五)循环嵌套题型讲解
- 前言
- C++循环嵌套题型讲解
- 第一题 包含数字的9
- 第二题 求出 e 的值
- 第三题 斐波那契数列
- 第四题 第 n 小的质数
- 第五题 水仙花数
前言
- 前面的题型里我们认识了C++里面的三大循环
- 本篇博客我们开始讲解C++循环嵌套题型
我的个人主页,欢迎来阅读我的其他文章
https://blog.csdn.net/2402_83322742?spm=1011.2415.3001.5343
我的C++算法竞赛篇文章专栏
欢迎来阅读指出不足
https://blog.csdn.net/2402_83322742/category_13001405.html?spm=1001.2014.3001.5482
C++循环嵌套题型讲解
第一题 包含数字的9
题目链接https://www.nowcoder.com/practice/0948f4f3344c452f843afd3585dd0f8d?tpId=290&tqId=320953&ru=/exam/oj&qru=/ta/beginner-programmers/question-ranking&sourceUrl=%2Fexam%2Foj
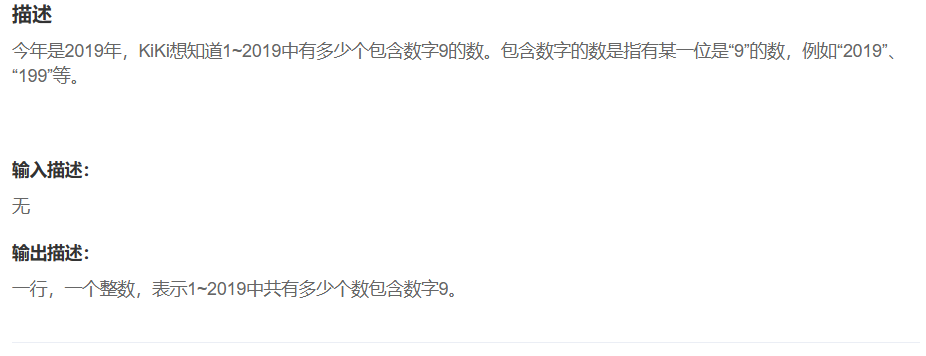
解题思路:
- 遍历范围:需统计
1~2019所有整数中包含数字9的数的个数,通过for循环遍历i从1到2019。 - 包含9的判断逻辑:对每个数
i,用while循环分解其每一位(n = i,通过n % 10取末位、n = n / 10去掉末位)。若某一位为9,则计数count++并通过break跳出该数的判断(避免重复计数)。 - 输出格式:遍历结束后,输出最终计数
count。
#include <iostream>
using namespace std;int main() {int count = 0;for (int i = 1;i<=2019;i++){int n = i;while(n){if( n % 10 == 9){count++;break;}n = n /10;}}cout << count ;return 0;
}
第二题 求出 e 的值
题目链接https://www.luogu.com.cn/problem/B2079
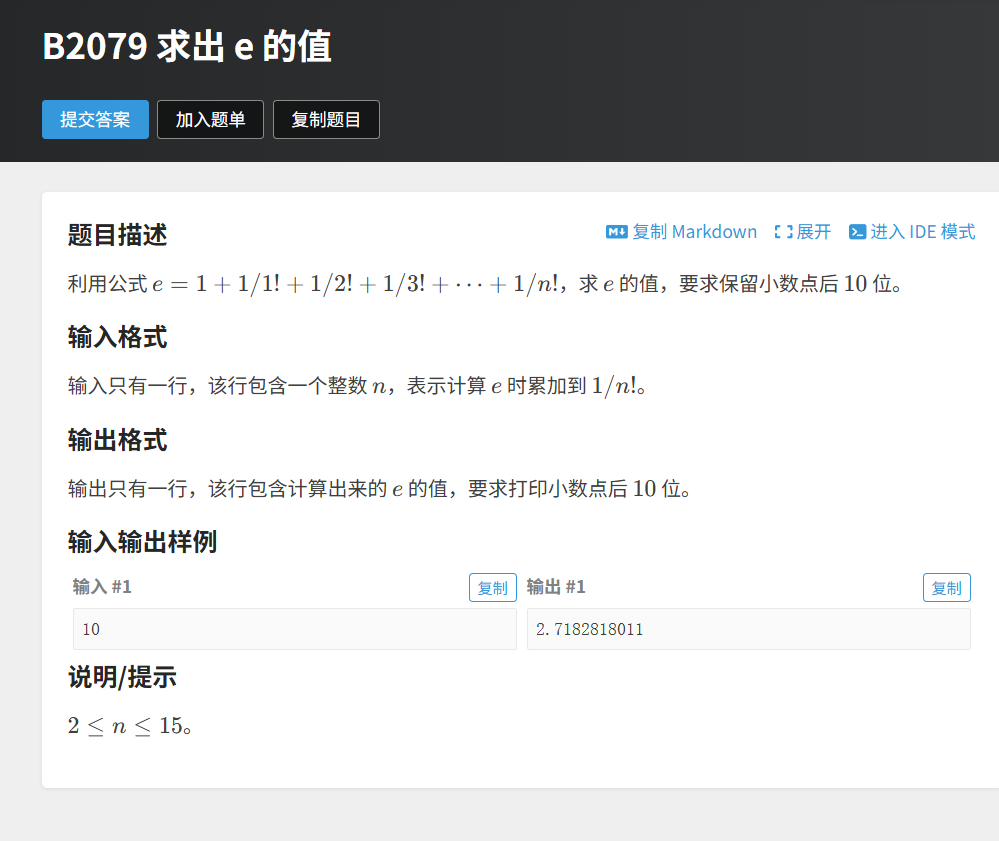
解题思路:
- 输入处理:用
cin读取整数n,确定需计算e的近似值的累加项数(共n+1项,包含0!)。 - 累加逻辑(嵌套循环):
- 外层
for循环控制累加次数(从1到n,对应1/1!到1/n!)。 - 内层
for循环计算当前项的阶乘(r = r * j,j从1到i),再将1.0 / r累加到sum(注意用1.0确保浮点运算)。
- 外层
- 输出格式:用
printf按%.10f格式输出保留 10 位小数的e近似值。
#include <iostream>
#include <cstdio>using namespace std;int main()
{int n;double sum = 1;cin >> n;for(int i = 1; i <= n; i++){long long r = 1;for(int j = 1; j <= i; j++){r *= j;}sum += 1.0 / r;}printf("%.10f\n", sum);return 0;
}
第三题 斐波那契数列
题目链接 https://www.luogu.com.cn/problem/B2064
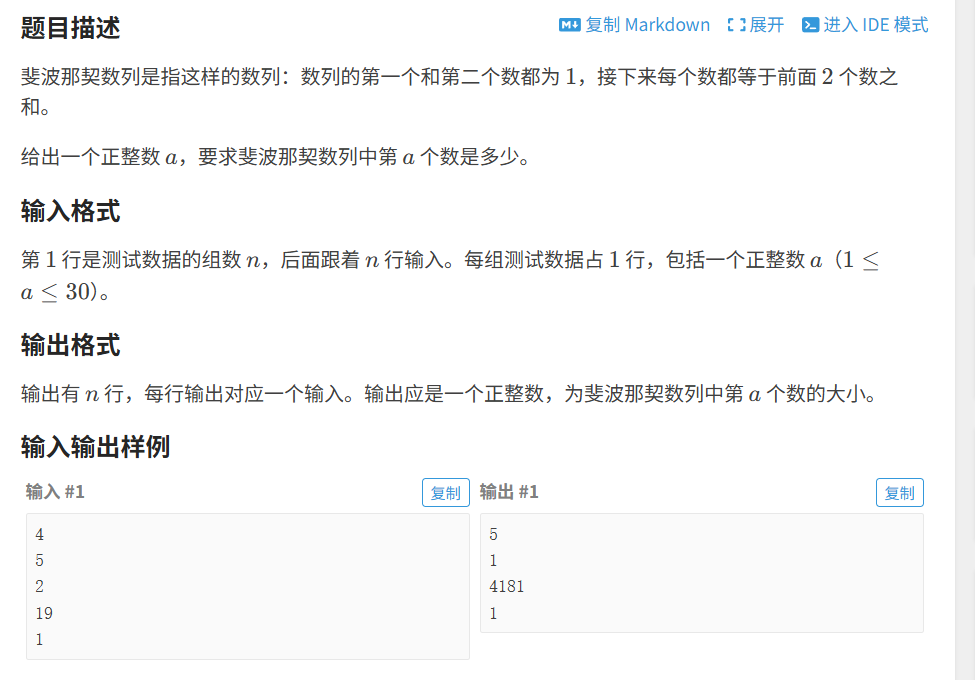
解题思路:
- 输入处理:先读取测试用例数
n,再通过while(n--)循环逐个读取需查询的斐波那契数列位置a。 - 斐波那契计算逻辑:
- 斐波那契数列前两项固定为
1, 1(x=1, y=1)。 - 若
a > 2,用while循环迭代计算:z = x + y(下一项),更新x = y、y = z,直到迭代到第a项。
- 斐波那契数列前两项固定为
- 输出格式:对每个查询的
a,输出对应的斐波那契数z。
#include <iostream>
using namespace std;int main()
{int n = 0;int a = 0;cin >> n;while(n--){cin >> a;// 计算第a个斐波那契数int x = 1;int y = 1;int z = 1;while (a > 2){z = x + y;x = y;y = z;a--;}cout << z << endl;}return 0;
}
第四题 第 n 小的质数
题目链接 https://www.luogu.com.cn/problem/B2085
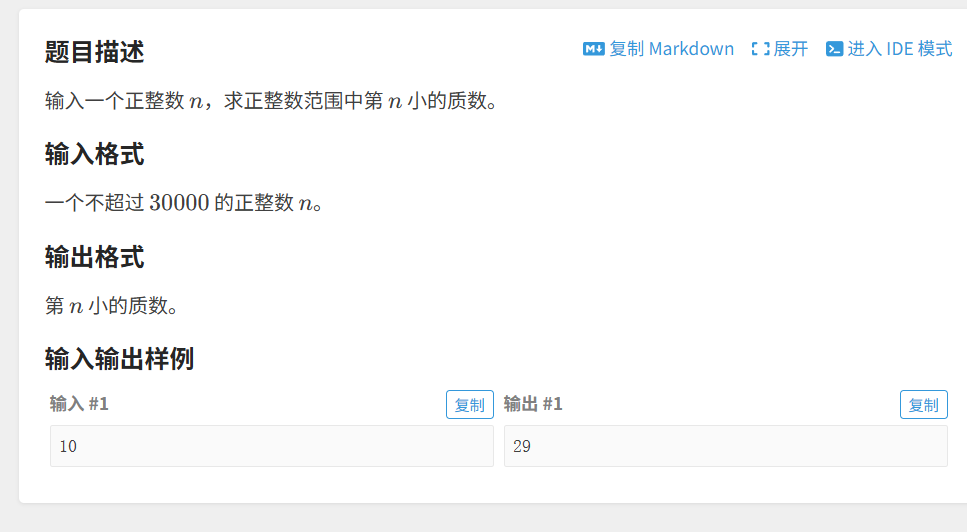
解题思路:
- 输入处理:用
cin读取整数n,表示需找第 n 个质数。 - 质数判断逻辑(循环嵌套):
- 外层
while(1)循环遍历数字i(从2开始,因为2是最小质数)。 - 内层
for循环通过j <= sqrt(i)优化判断:若i % j == 0,则i不是质数(flag=0);否则i是质数(flag=1)。 - 找到质数时
cnt++,当cnt == n时,跳出循环,此时i即为第n小的质数。
- 外层
- 输出格式:输出第
n小的质数i。
#include <iostream>
#include <cmath>
using namespace std;int main()
{int n;cin >> n;int i = 2;int cnt = 0; // 计数器while(1){// 判断i是否是素数int flag = 1; // 假设是素数for(int j = 2; j <= sqrt(i); j++){if(i % j == 0){flag = 0; // 不是素数break;}}if(flag == 1)cnt++;if(cnt == n)break;i++;}cout << i << endl;return 0;
}
第五题 水仙花数
题目链接 https://ybt.ssoier.cn/problem_show.php?pid=2029
解题思路:
- 遍历范围:需筛选
100~999的所有三位数,通过for循环遍历i从100到999。 - 水仙花数判断逻辑:
- 对每个数
i,用while循环分解其每一位(tmp = i,通过tmp % 10取末位、tmp = tmp / 10去掉末位)。 - 计算各位数字的立方和(
r += pow(tmp % 10, 3)),判断r是否等于原数i。
- 对每个数
- 输出格式:逐个输出符合条件的水仙花数
i。
#include <iostream>
#include <cmath>
using namespace std;int main()
{for(int i = 100; i <= 999; i++){int tmp = i;int r = 0;while(tmp){r += pow(tmp % 10, 3);tmp /= 10;}if(r == i)cout << i << endl;}return 0;
}
以上就是这篇博客的全部内容,下一篇我们将继续探索C++算法的更多精彩内容。
我的个人主页,欢迎来阅读我的其他文章
https://blog.csdn.net/2402_83322742?spm=1011.2415.3001.5343
我的C++算法竞赛篇文章专栏
欢迎来阅读指出不足
https://blog.csdn.net/2402_83322742/category_13001405.html?spm=1001.2014.3001.5482
| 非常感谢您的阅读,喜欢的话记得三连哦 |

——ChatInterface的多模态功能与附加输入输出)


 -> 配置构建(三))
——技术平台——共享平台)


)

有界面)



-Git篇)


)


—让大模型理解表格数据(列车信息表))