数据结构——查找（三、树形查找）

一、二叉排序树（BST）

1、二叉排序树的定义

构造一棵二叉排序树的目的并不是排序，而是提高查找、插入和删除关键字的速度

二叉排序树（也称二叉搜索树）或者是一颗空树，或者是具有以下性质的二叉树

1、若左子树非空，则左子树上所有结点的值均小于根节点的值

2、若右子树非空，则右子树上所有结点的值均大于根节点的值

3、左右子树分别是一颗二叉排序树

（右子树所有结点的值均大于左子树所有结点的值）

对二叉排序树进行中序遍历，可以得到一个递增的有序序列

2、二叉排序树的查找

二叉排序树的查找是从根节点开始，是一个递归的过程

二叉排序树的非递归查找算法 ，空间复杂度O(1)

//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//二叉排序树的非递归查找算法 
BSTNode *BST_Search(BSTree T, int key){while(T != NULL && key != T->key){ //若树空或等于根节点值，则结束循环if(key < T->key){       //小于，则在左子树上查找T = T->lchild;      //大于，则在右子树上查找}else{T = T->rchild;}}return T;
}

二叉排序树的递归查找算法 ，空间复杂度O(h)

//在二叉排序树中查找值为key的结点（递归实现）
BSTNode *BST_Search_Recursion(BSTree T, int key){if(T == NULL){return NULL;    //查找失败}if(key == T->key){return T;       //查找成功}else if(key < T->key){return BST_Search_Recursion(T->lchild, key);//在左子树中找}else{return BST_Search_Recursion(T->rchild, key);//在右子树中找}}

 3、二叉排序树的插入

二叉排序树是一颗动态树，在查找过程中，当树中不存在关键字值等于给定值的结点时进行插入。

若关键字的值小于根结点，则插入左子树；反之，插入右子树；

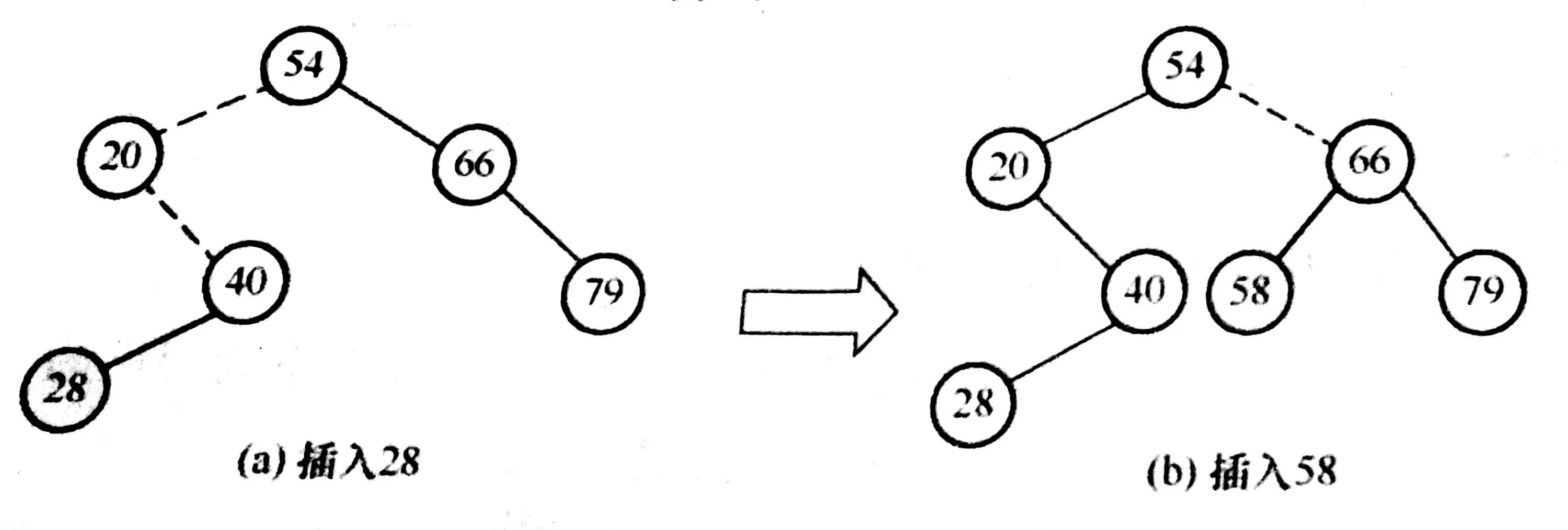
新插入的结点一定是一个叶节点，且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子

如图，虚线表示查找路径

在二叉排序树中插入关键值为key的新结点（递归实现）

注：树中存在相同关键字的结点会导致插入失败

//在二叉排序树中插入关键值为key的新结点（递归实现）
int BST_Insert(BSTree &T, int k){if(T == NULL){      //原树为空，新插入的结点为根节点T = (BSTree)malloc(sizeof(BSTNode)); T->key = k;T->lchild = T->rchild = NULL;return 1;       //返回1，插入成功}else if(k == T->key){ //树中存在相同关键字的结点，插入失败return 0;}else if(k < T->key){   //插入到T的左子树return BST_Insert(T->lchild, k);}else{                  //插入到T的右子树return BST_Insert(T->rchild, k);}
}

在二叉排序树中插入关键值为key的新结点（非递归实现）

//在二叉排序树中插入关键值为key的新结点（非递归实现）
int BST_Insert2(BSTree &T, int key) {BSTNode *newNode = (BSTNode*)malloc(sizeof(BSTNode)); // 创建新节点newNode->key = key;newNode->lchild = newNode->rchild = NULL;if (T == NULL) {  // 如果树为空，直接插入新节点作为根T = newNode;return 1; // 插入成功}BSTNode *parent = NULL;  // 用来记录父节点BSTNode *current = T;    // 当前节点从根开始while (current != NULL) {parent = current;  // 记录当前节点为父节点if (key == current->key) {free(newNode); // 如果树中已有相同的key，插入失败，释放新节点return 0;  // 插入失败}else if (key < current->key) {current = current->lchild;  // key 小于当前节点，移动到左子树}else {current = current->rchild;  // key 大于当前节点，移动到右子树}}// 在遍历到NULL时，插入新节点if (key < parent->key) {parent->lchild = newNode;  // 插入到父节点的左子树}else {parent->rchild = newNode;  // 插入到父节点的右子树}return 1;  // 插入成功
}

4、二叉排序树的构造

不同的输入序列会得到不同的二叉排序树

与二分查找判定树不同，二分查找仅适用于有序的顺序表，这也就意味着，同一个序列判定树唯一。

//按照str[]中的关键字序列建立二叉排序树
void create_BST(BSTree &T, int str[], int n){T = NULL;       //初始时T为空树int i = 0;while(i < n){   //依次将每个关键字插入到二叉排序树中BST_Insert(T, str[i]);i++;}
}

5、二叉排序树的删除

①若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质;
②若结点z只有一棵左子树或右子树，则让z的子树替代z的位置；
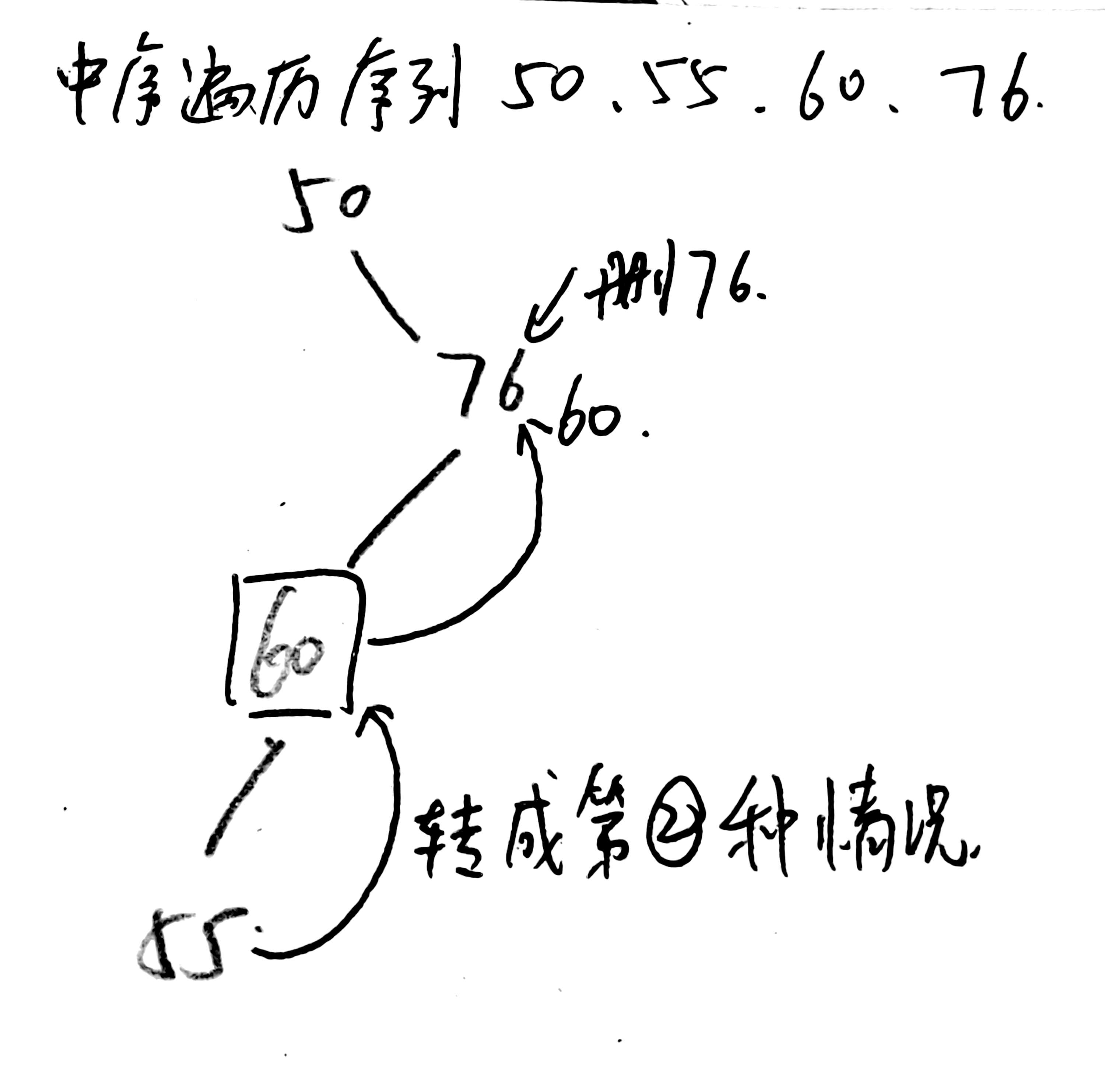
③若结点z有左、右两棵子树，则进行中序遍历，让z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（直接前驱），这样就转换成了第一或第二种的情况。

如图，删除76，为第③种情况，找到直接前驱，将直接前驱的值60替代76。而后转变为删除60，此时转变成第②种情况，直接让60的左子树（55）替代60，并释放55即可。

在二叉排序树中删除关键值为key的结点（递归实现）

// 查找二叉树中的最小结点（即直接后继）
BSTNode* findMin(BSTree T) {while (T && T->lchild) {T = T->lchild;}return T;
}// 查找二叉树中的最大结点（即直接前驱）
BSTNode* findMax(BSTree T) {while (T && T->rchild) {T = T->rchild;}return T;
}// 在二叉排序树中删除关键值为key的结点（递归实现）
BSTree BST_Delete(BSTree T, int key) {if (T == NULL) {return T;  // 树为空，直接返回}// 如果key小于当前结点的key，则在左子树中删除if (key < T->key) {T->lchild = BST_Delete(T->lchild, key);}// 如果key大于当前结点的key，则在右子树中删除else if (key > T->key) {T->rchild = BST_Delete(T->rchild, key);}// 找到要删除的结点else {// 1. 删除的是叶结点if (T->lchild == NULL && T->rchild == NULL) {free(T);  // 直接释放该结点return NULL;  // 返回NULL，删除该结点}// 2. 删除的结点只有一个子树else if (T->lchild == NULL) {  // 只有右子树BSTNode* temp = T;T = T->rchild;  // 用右子树替代free(temp);}else if (T->rchild == NULL) {  // 只有左子树BSTNode* temp = T;T = T->lchild;  // 用左子树替代free(temp);}// 3. 删除的结点有两个子树else {// 找到当前结点的直接后继（右子树中的最小节点）BSTNode* temp = findMin(T->rchild);T->key = temp->key;  // 用后继节点替代当前节点T->rchild = BST_Delete(T->rchild, temp->key);  // 删除后继结点}}return T;
}

6、二叉排序树的查找效率分析

二叉排序树的查找效率取决于树的高度。

若二叉排序树左右子树的高度只差的绝对值不超过1（即平衡二叉树），它的平均查找长度为O(log_{2}n)成正比。

在最坏的情况下，若输入序列为有序的，则会形成只有右孩子的单支树，此时树高为n，即平均查找长度为(n+1)/2

在查找方面，二叉排序树和二分查找的性能差不多，但因为二叉排序树与输入序列有关，所以同一个序列两种方法的平均查找长度（即效率）存在不同。

插入删除结点维护有序性而言，二叉排序树只需要移动指针，时间复杂度为O(log_{2}n）

而二分查找本身为有序顺序表，插入或删除需要移动大量元素，时间复杂度为O(n)

二、平衡二叉树（AVL)

平衡因子=左子树高-右子树高

平衡二叉树——平衡因子的绝对值不超过1

1、平衡二叉树的插入

插入一个结点会造成4种情况，处理方法可使用口诀

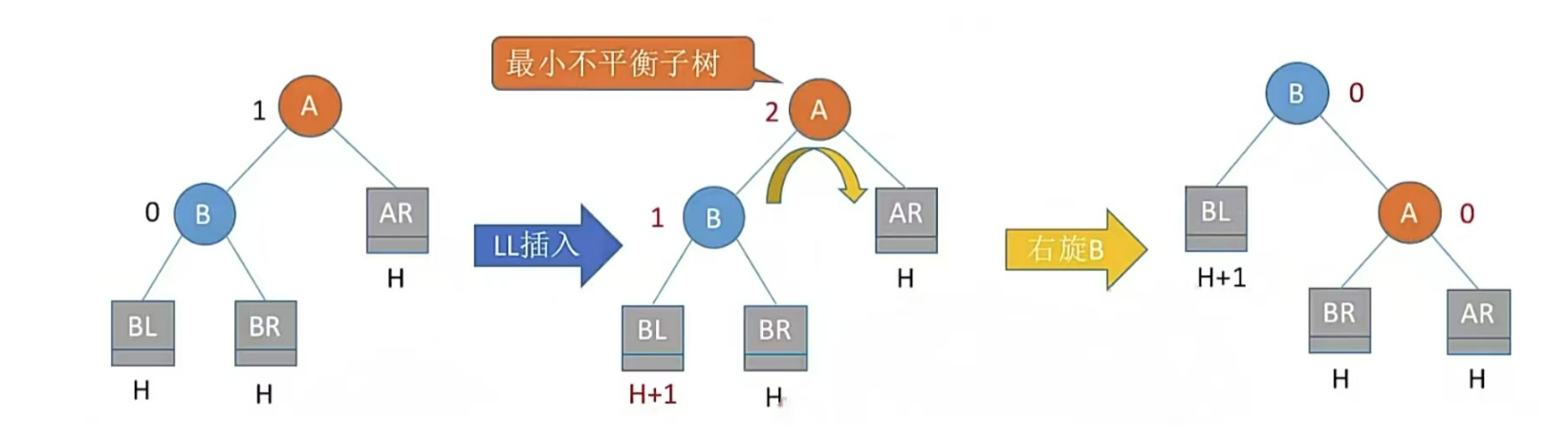
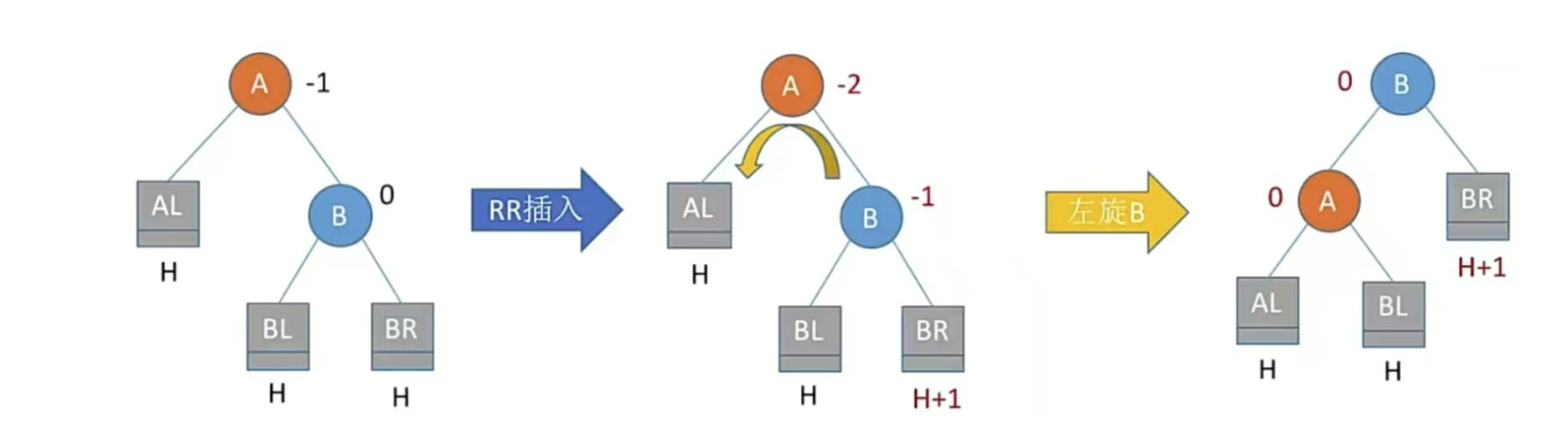
只有左孩子右上旋，只有右孩子左上旋

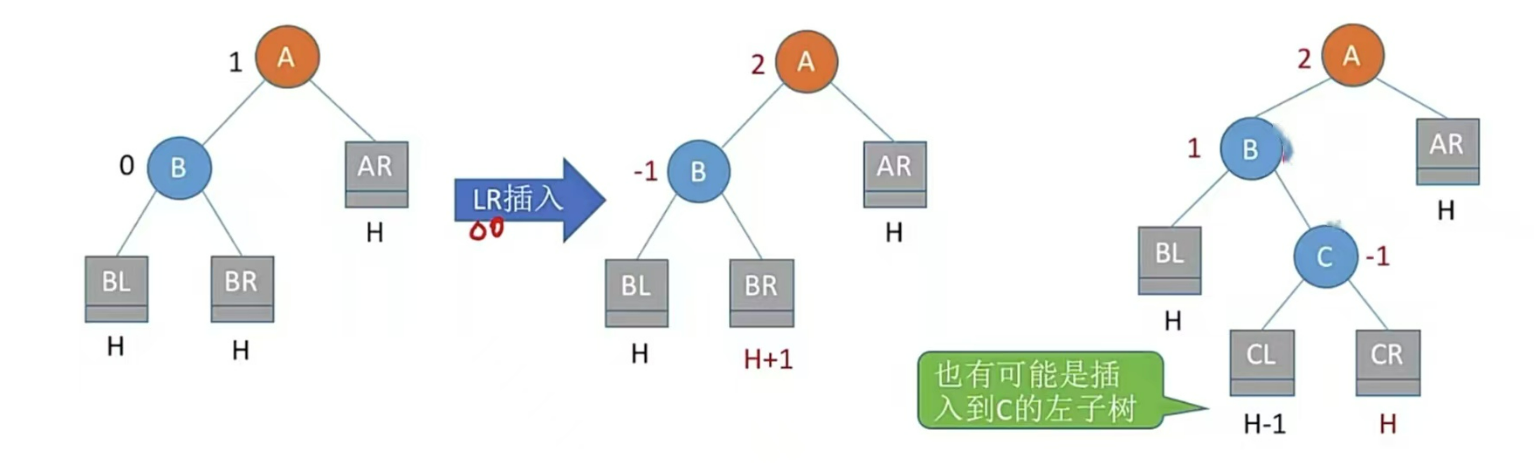
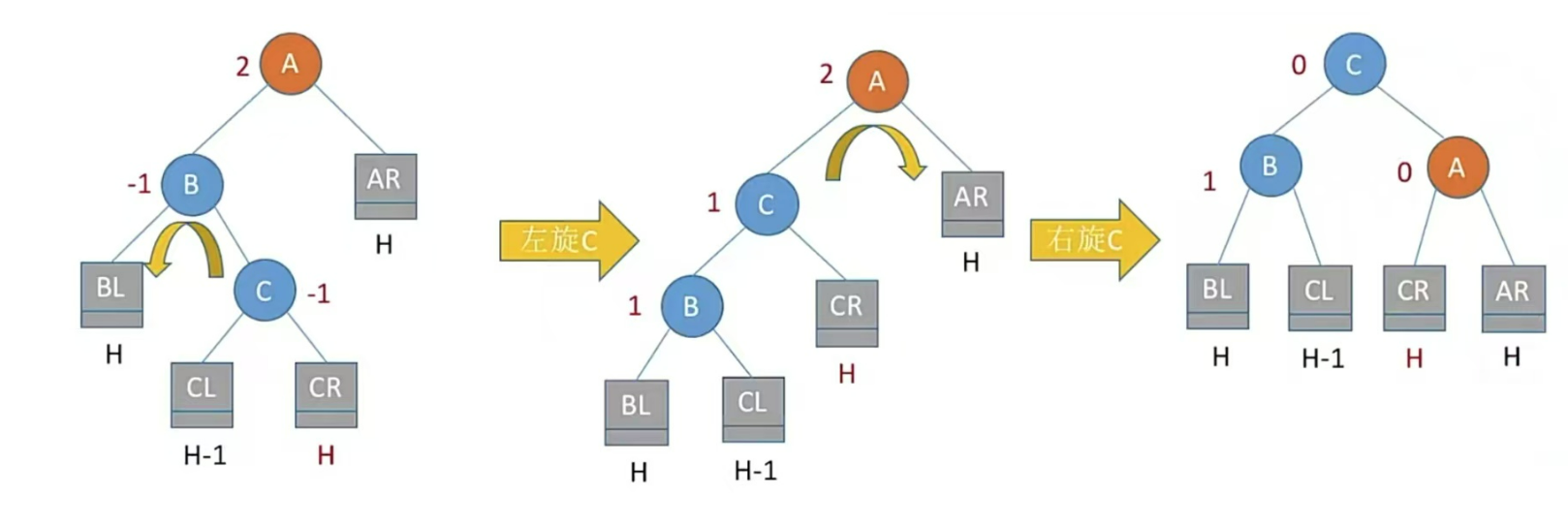
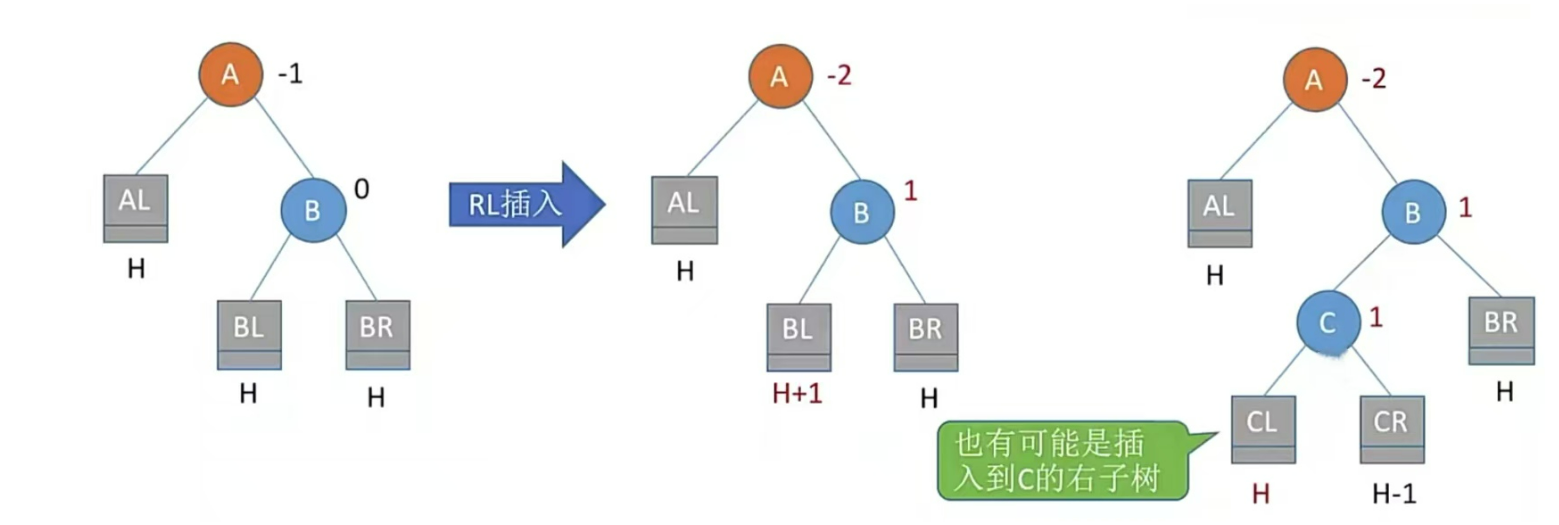
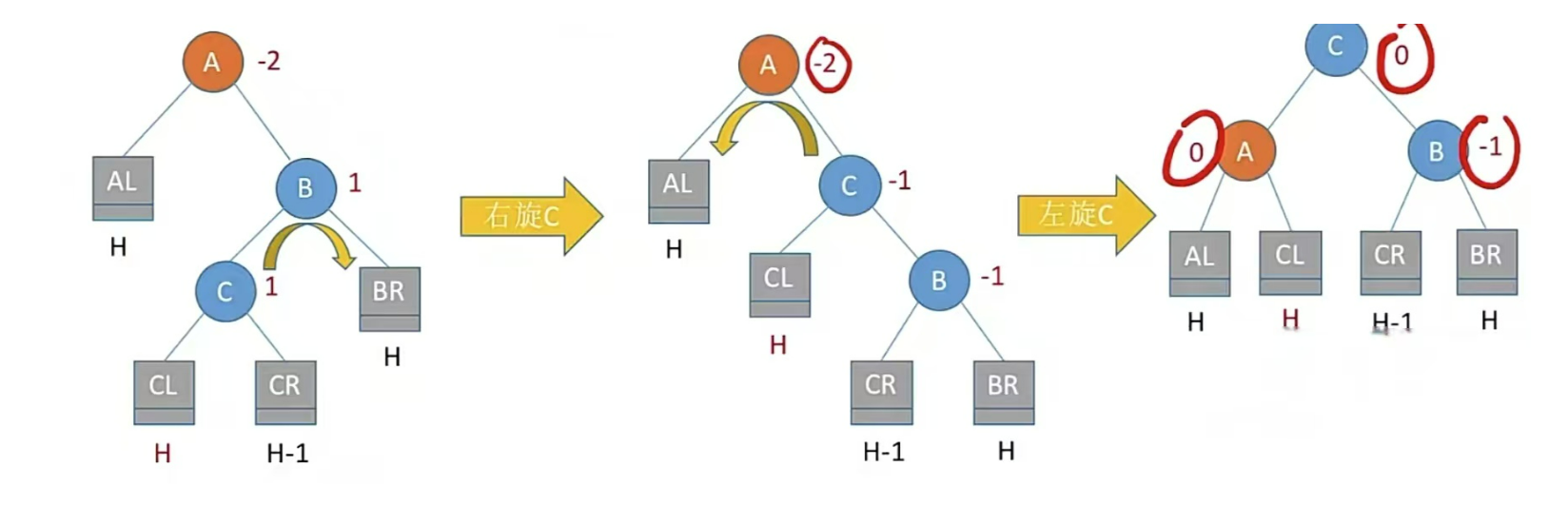
LL、RR儿子旋转一次；LR、RL儿子、孙子各旋转一次（共两次）

RR型，右孩子的右子树插入结点，即儿子右上旋转

LR型，左孩子的右子树插入结点，即孙子左上旋转，儿子右上旋

RL型，右孩子的左子树插入结点，即孙子右上旋转，儿子左上旋

注：LR和RL旋转时，新结点究竟插入C的左子树还是右子树不影响旋转结果。最终保证最底层没有H+1

2、平衡二叉树的删除

  1. 删除结点（方法同“二叉排序树”）；
  2. 一路向北找到最小不平衡子树，找不到就结束；
  3. 找最小不平衡子树下，“个头”最高的儿子、孙子；
  4. 根据孙子的位置，调整平衡（LL/RR/LR/RL）；
  5. 如果不平衡向上传导，回到第2条。

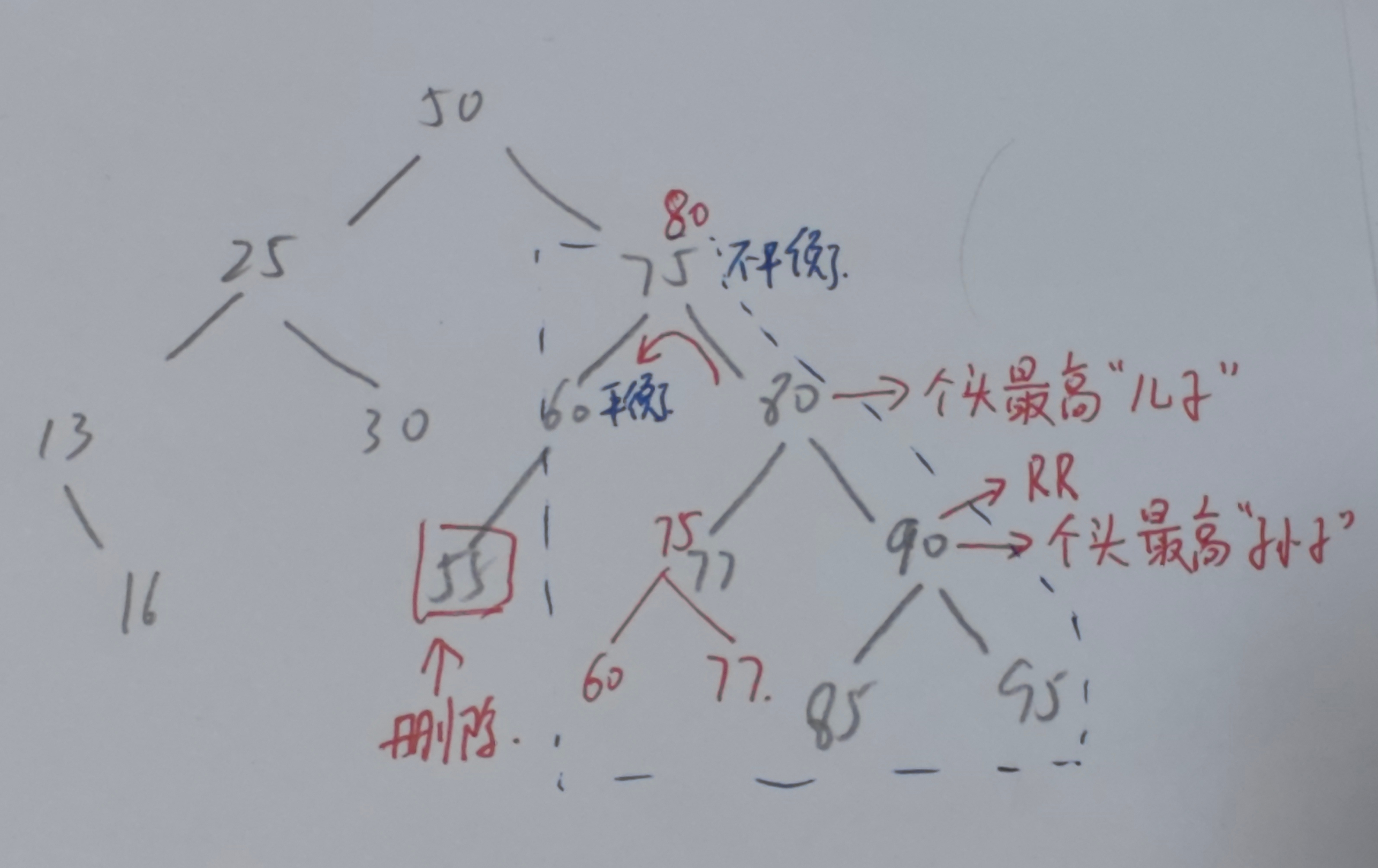
如图，红笔所示为删除后的替换

  1. 若要删除55，此时55为叶子结点，直接删除
  2. 删除之后一路向北，60仍然平衡，左右子树均为空；75不平衡，左子树高为1，右子树高为3
  3. 找个头最高的儿子为80，个头最高的孙子为90
  4. 孙子90位于爷爷80的RR型，只需要儿子进行左上旋
  5. 调整完毕，向北探查，发现50也平衡，调整结束

3、平衡二叉树的查找效率

假设以n_{h}表示深度为h的平衡树中含有的最少结点数，则：

有n_{0}= 0，n_{1}= 1，n_{2}= 2，并且有n_{h} = n_{h-1} + n_{h-2} + 1

含有n个结点的平衡二叉树的最大深度有递推式推出，即O(log_{2}n）

最小深度即满二叉树情况

三、红黑树

平衡二叉树（AVL）：在执行插入或删除操作时，容易破坏其平衡性，因此需要频繁调整树拓扑结构。例如，当插入操作导致不平衡时，系统需要先计算平衡因子，定位最小不平衡子树（这一过程耗时较大），然后执行LL/RR/LR/RL等旋转操作来恢复平衡。

红黑树（RBT）：在插入或删除操作时，通常能够保持其红黑特性，因此不需要频繁调整树结构。即使需要调整，也往往能在常数时间内完成操作。

在实际使用中，平衡二叉树适用于以查为主，很少插入/删除的应用场景；而红黑树适用于频繁插入/删除的场景，实用性更强。

1、红黑树的定义

红黑树本质上是二叉排序树

但是在插入时可以插入重复值

满足如下性质的二叉排序树即为红黑树：

  1. 满足 左子树结点值 ≤ 根节点值 ≤ 右子树结点值；
  2. 每个结点或是红色的，或是黑色的；
  3. 根节点是黑色的；
  4. 叶结点（外部结点、NULL结点、失败结点）均是黑色的；
  5. 不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色）；
  6. 对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同。

左根右，根叶黑，不红红，黑路同

红黑树的结点定义

struct RBNode{          //红黑树的结点定义int key;            //关键字的值RBNode* parent;     //双亲结点指针RBNode* lchild;     //左孩子指针RBNode* rchild;     //右孩子指针int color;          //结点颜色，如：可用0/1表示黑/红，也可以使用枚举型enum表示颜色
};

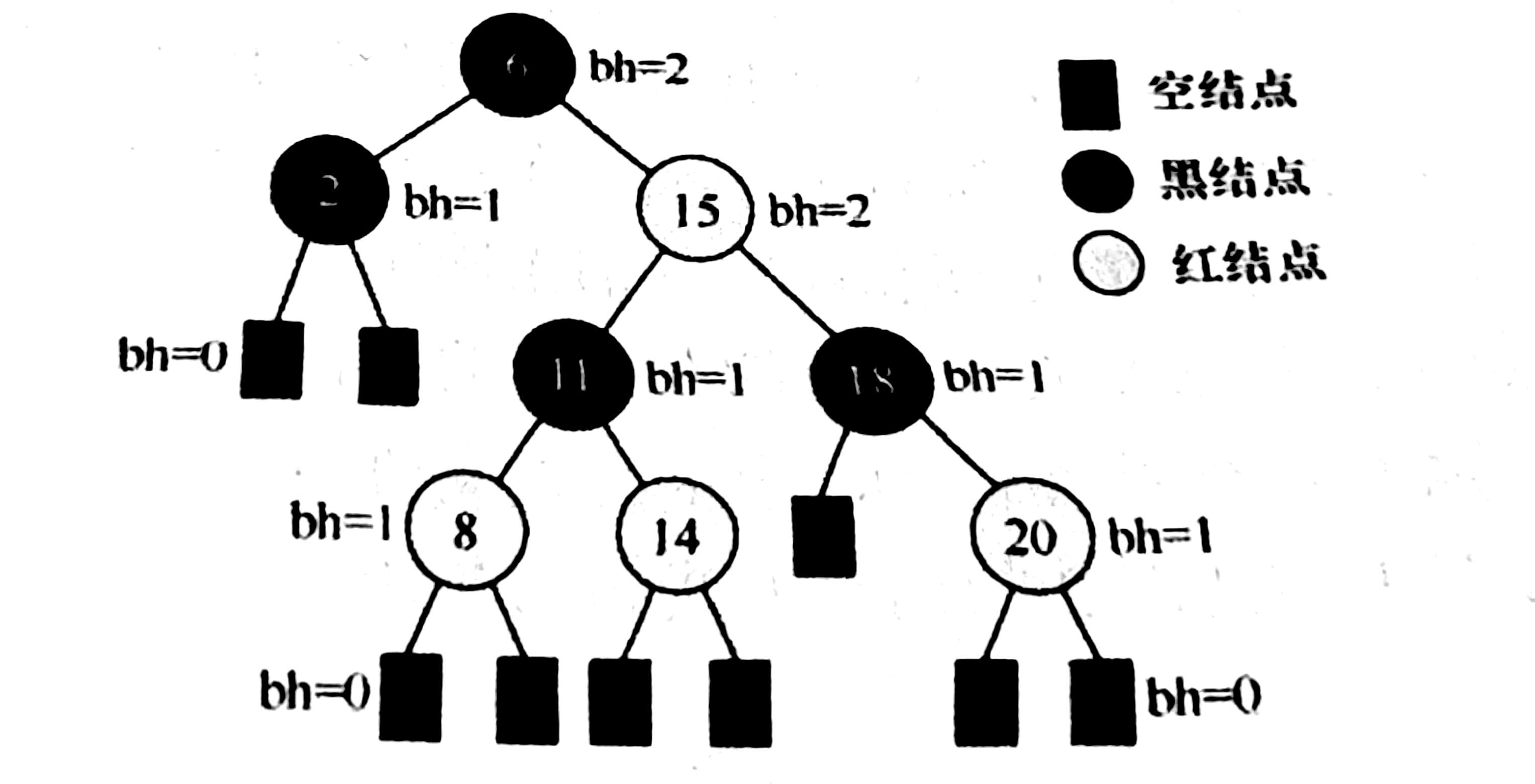
1、从某个结点（不包含该结点）出发，到达一个叶结点的任意一个简单路径上的黑结点总数称为该结点的黑高。（由性质6黑路同确定）

2、从根结点到叶结点的最长路径不大于最短路径的两倍。

3、根结点黑高为h，至少2^{h}-1内部结点， 即只有黑结点，并且满树的情况。（由性质56确定），最多是2^{2h}-1

4、由于红结点最多间隔插入黑结点，所以黑高h\geq \frac{h}{2}，于是n\geq 2^{h/2}+1

2、红黑树的插入

1、先查找，确定插入位置（原理同二叉排序树），插入新结点
2、新结点是 根——染为黑色
3、新结点 非根——染为红色

  1. 若插入新结点后依然满足红黑树定义，则插入结束
  2. 若插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义

                  黑叔：旋转+染色

                          LL型：右单旋，父换爷+染色

                          RR型：左单旋，父换爷+染色

                          LR型：左、右双旋，儿换爷+染色

                          RL型：右、左双旋，儿换爷+染色

                  红叔：染色+变新

                          叔父爷染色，爷变为新结点

红黑树的插入，更多注意不红红的情况，而后是根叶黑，至于左根右、黑路同，在插入的时候规则就考虑了。

四、完整代码实现

1、二叉排序树部分

#include <iostream>
#include <cstdlib>using namespace std;//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//二叉排序树的非递归查找算法 
BSTNode *BST_Search(BSTree T, int key){while(T != NULL && key != T->key){ //若树空或等于根节点值，则结束循环if(key < T->key){       //小于，则在左子树上查找T = T->lchild;      //大于，则在右子树上查找}else{T = T->rchild;}}return T;}//在二叉排序树中查找值为key的结点（递归实现）
BSTNode *BST_Search_Recursion(BSTree T, int key){if(T == NULL){return NULL;    //查找失败}if(key == T->key){return T;       //查找成功}else if(key < T->key){return BST_Search_Recursion(T->lchild, key);//在左子树中找}else{return BST_Search_Recursion(T->rchild, key);//在右子树中找}}//在二叉排序树中插入关键值为key的新结点（递归实现）
int BST_Insert(BSTree &T, int k){if(T == NULL){      //原树为空，新插入的结点为根节点T = (BSTree)malloc(sizeof(BSTNode)); T->key = k;T->lchild = T->rchild = NULL;return 1;       //返回1，插入成功}else if(k == T->key){ //树中存在相同关键字的结点，插入失败return 0;}else if(k < T->key){   //插入到T的左子树return BST_Insert(T->lchild, k);}else{                  //插入到T的右子树return BST_Insert(T->rchild, k);}
}//在二叉排序树中插入关键值为key的新结点（非递归实现）
int BST_Insert2(BSTree &T, int key) {BSTNode *newNode = (BSTNode*)malloc(sizeof(BSTNode)); // 创建新节点newNode->key = key;newNode->lchild = newNode->rchild = NULL;if (T == NULL) {  // 如果树为空，直接插入新节点作为根T = newNode;return 1; // 插入成功}BSTNode *parent = NULL;  // 用来记录父节点BSTNode *current = T;    // 当前节点从根开始while (current != NULL) {parent = current;  // 记录当前节点为父节点if (key == current->key) {free(newNode); // 如果树中已有相同的key，插入失败，释放新节点return 0;  // 插入失败}else if (key < current->key) {current = current->lchild;  // key 小于当前节点，移动到左子树}else {current = current->rchild;  // key 大于当前节点，移动到右子树}}// 在遍历到NULL时，插入新节点if (key < parent->key) {parent->lchild = newNode;  // 插入到父节点的左子树}else {parent->rchild = newNode;  // 插入到父节点的右子树}return 1;  // 插入成功
}//按照str[]中的关键字序列建立二叉排序树
void create_BST(BSTree &T, int str[], int n){T = NULL;       //初始时T为空树int i = 0;while(i < n){   //依次将每个关键字插入到二叉排序树中BST_Insert(T, str[i]);i++;}
}// 查找二叉树中的最小结点（即直接后继）
BSTNode* findMin(BSTree T) {while (T && T->lchild) {T = T->lchild;}return T;
}// 查找二叉树中的最大结点（即直接前驱）
BSTNode* findMax(BSTree T) {while (T && T->rchild) {T = T->rchild;}return T;
}// 在二叉排序树中删除关键值为key的结点（递归实现）
BSTree BST_Delete(BSTree T, int key) {if (T == NULL) {return T;  // 树为空，直接返回}// 如果key小于当前结点的key，则在左子树中删除if (key < T->key) {T->lchild = BST_Delete(T->lchild, key);}// 如果key大于当前结点的key，则在右子树中删除else if (key > T->key) {T->rchild = BST_Delete(T->rchild, key);}// 找到要删除的结点else {// 1. 删除的是叶结点if (T->lchild == NULL && T->rchild == NULL) {free(T);  // 直接释放该结点return NULL;  // 返回NULL，删除该结点}// 2. 删除的结点只有一个子树else if (T->lchild == NULL) {  // 只有右子树BSTNode* temp = T;T = T->rchild;  // 用右子树替代free(temp);}else if (T->rchild == NULL) {  // 只有左子树BSTNode* temp = T;T = T->lchild;  // 用左子树替代free(temp);}// 3. 删除的结点有两个子树else {// 找到当前结点的直接后继（右子树中的最小节点）BSTNode* temp = findMin(T->rchild);T->key = temp->key;  // 用后继节点替代当前节点T->rchild = BST_Delete(T->rchild, temp->key);  // 删除后继结点}}return T;
}// 在二叉排序树中删除关键值为key的结点（非递归实现）
BSTree BST_Delete2(BSTree T, int key) {BSTNode* parent = NULL;BSTNode* current = T;while (current != NULL && current->key != key) {parent = current;if (key < current->key) {current = current->lchild;} else {current = current->rchild;}}// 如果树中没有该结点if (current == NULL) {return T;  // 不删除任何结点}// 删除的结点有两个子树if (current->lchild != NULL && current->rchild != NULL) {// 找到右子树中的最小结点作为后继BSTNode* successorParent = current;BSTNode* successor = current->rchild;while (successor->lchild != NULL) {successorParent = successor;successor = successor->lchild;}// 替换当前结点的值为后继结点的值current->key = successor->key;// 删除后继结点if (successorParent->lchild == successor) {successorParent->lchild = successor->rchild;} else {successorParent->rchild = successor->rchild;}free(successor);}// 删除的结点没有左子树，只有右子树else if (current->lchild == NULL) {if (parent == NULL) { // 如果删除的是根结点T = current->rchild;} else if (parent->lchild == current) {parent->lchild = current->rchild;} else {parent->rchild = current->rchild;}free(current);}// 删除的结点没有右子树，只有左子树else if (current->rchild == NULL) {if (parent == NULL) { // 如果删除的是根结点T = current->lchild;} else if (parent->lchild == current) {parent->lchild = current->lchild;} else {parent->rchild = current->lchild;}free(current);}return T;
}void inorderTraversal(BSTree T) {if (T != NULL) {inorderTraversal(T->lchild);cout << T->key << " ";inorderTraversal(T->rchild);}
}int main() {BSTree T = NULL;int keys[] = {50, 30, 70, 20, 40, 60, 80};int n = sizeof(keys) / sizeof(keys[0]);// 创建二叉排序树create_BST(T, keys, n);// 打印树的中序遍历cout << "中序遍历输出：";inorderTraversal(T);cout << endl;// 查找某个元素int searchKey = 40;BSTNode* result = BST_Search(T, searchKey);if (result != NULL) {cout << "找到节点：" << result->key << endl;} else {cout << "未找到节点" << endl;}// 递归查找result = BST_Search_Recursion(T, searchKey);if (result != NULL) {cout << "递归查找找到节点：" << result->key << endl;} else {cout << "递归查找未找到节点" << endl;}// 删除一个结点并展示中序遍历int deleteKey = 70;cout << "删除结点 " << deleteKey << endl;T = BST_Delete(T, deleteKey);inorderTraversal(T);cout << endl;return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/web/91931.shtml
繁体地址，请注明出处：http://hk.pswp.cn/web/91931.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

八股——Kafka相关

八股——Kafka相关

文章目录1、 消息队列的作用什么&#xff1f;思&#xff1a;消息队列是什么?消息队列的定义消息队列的工作原理消息队列的作用消息队列的常见类型消息队列的简单例子2、Kafka 集群的架构是什么样子的&#xff1f;3、Kafka 消费者组和生产者组是什么&#xff1f;定义与核心作用…
阅读更多...
墨者学院SQL手工注入漏洞测试(MySQL数据库)题目，纯手工注入教程

墨者学院SQL手工注入漏洞测试(MySQL数据库)题目，纯手工注入教程

打开练习手工注入的靶场，发现此时为一个登录页面，我们先试着登录看看注入点在不在登录页面 使用用户：or 1=1# 密码：admin123；尝试登录，发现显示错误后直接弹回原页面，无sql报错相关语句，这里不存在sql注入点 一：判断注入点以及猜测是否有注入 此时点击这里的动态页面…
阅读更多...
[硬件电路-140]：模拟电路 - 信号处理电路 - 锁定放大器概述、工作原理、常见芯片、管脚定义

[硬件电路-140]：模拟电路 - 信号处理电路 - 锁定放大器概述、工作原理、常见芯片、管脚定义

一、锁定放大器概述锁定放大器&#xff08;Lock-in Amplifier&#xff09;是一种基于相干检测技术的高灵敏度测量仪器&#xff0c;通过将待测信号与参考信号进行同步处理&#xff0c;从强噪声中提取微弱信号并精确测量其振幅与相位。其核心优势包括&#xff1a;信噪比提升&…
阅读更多...
下载 | Windows Server 2025官方原版ISO映像！(7月更新、标准版、数据中心版、26100.4652)

下载 | Windows Server 2025官方原版ISO映像！(7月更新、标准版、数据中心版、26100.4652)

⏩ 资源A066_Windows_Server_2025系统映像&#x1f536; Windows Server 2025官方原版ISO映像&#xff0c;7月更新版已放出。提供来自微软官方每月更新的ISO原版映像&#xff0c;内部包含了标准版和数据中心版&#xff0c;可选择无GUI界面版或桌面体验版&#xff0c;满足不同部…
阅读更多...
Go 语言模糊测试 (Fuzz Testing) 深度解析与实践

Go 语言模糊测试 (Fuzz Testing) 深度解析与实践

学习一个知识&#xff0c;要先了解它的来源 1. 模糊测试的诞生&#xff1a;Barton Miller 的故事 “Fuzz”一词起源于1988年&#xff0c;由威斯康星大学麦迪逊分校的Barton Miller教授及其研究生团队在一个高级操作系统课程项目中提出 。这个概念的诞生颇具戏剧性。Miller教授在…
阅读更多...
【软考和软著】

【软考和软著】

一、&#x1f4ab; 杭州E类人才政策 在这里插入图片描述 二、人才认定标准 三、关于软考 1、什么是软考&#xff1f; 软考指的是“计算机技术与软件专业技术资格&#xff08;水平&#xff09;考试”。计算机软件资格考试是由国家人力资源和社会保障部、工业和信息化部领导下…
阅读更多...
「源力觉醒 创作者计划」开源大模型重构数智文明新范式

「源力觉醒 创作者计划」开源大模型重构数智文明新范式

起来轻松玩转文心大模型吧一文心大模型免费下载地址&#xff1a;https://ai.gitcode.com/paddlepaddle/ERNIE-4.5-VL-424B-A47B-Paddle开源大模型的崛起与AI幻觉挑战&#xff1a;中国AI发展的双重使命 ——从技术追赶到生态引领的跨越之路一、开源大模型&#xff1a;重构数智文…
阅读更多...
政务云数智化转型：灵雀云打造核心技术支撑能力

政务云数智化转型：灵雀云打造核心技术支撑能力

政务云数智化转型进行时&#xff0c;亟需体系升级政务信息化作为政府治理与服务的重要支撑&#xff0c;业务呈现出政策性强、数据敏感度高、系统复杂度高、服务连续性要求严等特点&#xff0c;对IT系统提出了极高要求&#xff1a;不仅需支撑高并发、高可用的政务应用&#xff0…
阅读更多...
软件测试自学之路

软件测试自学之路

别找了&#xff01;2025B站最全最细的软件测试教程&#xff0c;7天从零基础小白到精通软件测试&#xff0c;学完即上岗&#xff01;自学软件测试对于小白来说还是有一定的难度&#xff0c;各种专业术语的不熟悉&#xff0c;各种电脑操作的不熟悉&#xff0c;有时候要安装一个学…
阅读更多...
备案期间老网站有什么要求

备案期间老网站有什么要求

老网站的内容必须符合法律法规和互联网管理规定。这可不是开玩笑的事儿&#xff0c;相关部门对于网站内容的审核可是相当严格的。比如说&#xff0c;不能有违法犯罪、色情低俗、虚假信息等不良内容。根据互联网信息管理专家的建议&#xff0c;网站内容应该积极健康、真实准确。…
阅读更多...
Java数组转换为逗号分隔字符串的方法

Java数组转换为逗号分隔字符串的方法

Java数组转换为逗号分隔字符串的方法 在Java中&#xff0c;将数组转换为逗号分隔的字符串有几种常用方法&#xff0c;以下是清晰可靠的实现方案&#xff1a; 方法1&#xff1a;使用Arrays.toString() 字符串处理&#xff08;通用型&#xff09; import java.util.Arrays;publi…
阅读更多...
抗辐照DCDC与MCU在核环境监测设备中的集成应用

抗辐照DCDC与MCU在核环境监测设备中的集成应用

摘要核环境监测设备对保障核设施安全、保护环境与人员健康意义重大&#xff0c;需在复杂恶劣的核环境中稳定运行。电子设备易受核辐射影响产生单粒子效应等故障&#xff0c;选用具备抗辐照能力的DCDC与MCU芯片至关重要。本文结合实际测试数据&#xff0c;深入探讨抗辐照DCDC与M…
阅读更多...
C语言-指针[指针数组和数组指针]

C语言-指针[指针数组和数组指针]

知识重复变量指针&#xff1a;变量最小的地址值&#xff08;首地址&#xff09;&#xff0c;本质是地址、指针指针变量&#xff1a;存储指针的变量&#xff0c;本质是变量&&#xff1a;取地址运算符&#xff08;取址符、取地址符&#xff09;&#xff0c;获取变量、数组等的…
阅读更多...
NX982NX984美光固态闪存NX992NY102

NX982NX984美光固态闪存NX992NY102

NX982NX984美光固态闪存NX992NY102技术革新引领存储革命——深度拆解美光NX系列固态闪存在数字化浪潮席卷全球的当下&#xff0c;数据存储已成为支撑人工智能、云计算与物联网等前沿领域的核心基础设施。作为行业标杆企业&#xff0c;美光科技推出的NX系列固态闪存产品&#xf…
阅读更多...
Elasticsearch 集群管理核心 API 指南：健康、状态、分片诊断与运维实战

Elasticsearch 集群管理核心 API 指南：健康、状态、分片诊断与运维实战

一、集群健康状态 API (_cluster/health) 获取集群的总体健康状况&#xff0c;是监控的首要指标。 GET http://192.168.130.61:9200/_cluster/health响应字段解析 curl http://192.168.130.61:9200/_cluster/health 2>/dev/null |jq {"cluster_name": "E…
阅读更多...
Three.js 与 WebXR：初识 VR/AR 开发

Three.js 与 WebXR：初识 VR/AR 开发

引言 WebXR 是现代 Web 技术的重要组成部分&#xff0c;允许开发者通过浏览器创建虚拟现实&#xff08;VR&#xff09;和增强现实&#xff08;AR&#xff09;体验。结合 Three.js 的强大渲染能力&#xff0c;WebXR 可以轻松构建沉浸式 3D 场景。本文将介绍如何使用 Three.js 和…
阅读更多...
Kubernetes架构概览

Kubernetes架构概览

目录 专栏介绍 作者与平台 您将学到什么&#xff1f; 学习特色 Kubernetes架构概览 1.1 Kubernetes简介 1.2 基本架构 1.3 主要组件 1.4 核心功能 组件架构图解 2.1 控制平面组件详解 2.1.1 kube-apiserver 2.1.2 etcd 2.1.3 kube-scheduler 2.1.4 kube-controll…
阅读更多...
前端技术栈查缺补漏

前端技术栈查缺补漏

前端技术栈涵盖广泛&#xff0c;涉及多个领域和技术方向。以下是全面的分类总结&#xff0c;帮助你对前端技术生态有系统化的了解&#xff1a;一、核心基础HTML/CSS HTML5&#xff08;语义化标签、Web Components&#xff09;CSS3&#xff08;Flexbox/Grid、动画、变量、BEM/SM…
阅读更多...
文明7|席德·梅尔的文明VII PC/手机双端 模拟器版（Sid Meier’s Civilization VII）免安装中文版

文明7|席德·梅尔的文明VII PC/手机双端 模拟器版（Sid Meier’s Civilization VII）免安装中文版

网盘链接&#xff1a; 文明7|席德梅尔的文明VII 免安装中文版 名称&#xff1a;文明7|席德梅尔的文明VII PC/手机双端 模拟器版 免安装中文版 描述&#xff1a;这款策略神作重新定义了"历史蝴蝶效应"&#xff01; 《文明7》的"文明基因"系统让每个选择都刻…
阅读更多...
C#模式匹配用法与总结

C#模式匹配用法与总结

1. 模式匹配概述​​ 模式匹配是C# 7.0引入的机制&#xff0c;用于检查数据的类型、值或结构&#xff0c;并提取信息。通过is表达式、switch语句/表达式实现&#xff0c;显著简化条件逻辑&#xff0c;提升代码可读性和安全性。 ​​核心优势​​&#xff1a; ​​简洁性​​&…
阅读更多...
最新文章

Copyright @ 2022~2023