有效介电常数:

如果导体的横截面被介质完全包裹，位于导体之间的电力线(如带状线)就会感受到相同的介电常数。然而，对于微带线、双绞线或共面线，导体周围的介质不是均匀的，所以一些电力线穿过空气，而另一些则穿过介质。图5.10示例了微带线的电力线。

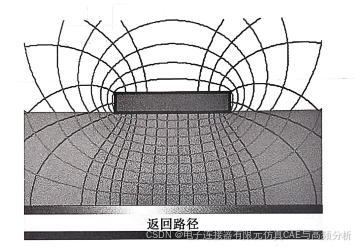
导体之间绝缘材料的存在，使其电容量比导体之间没有介质材料时增大了。若导体之间及导体周围的绝缘材料是均匀分布的，如带状线，则材料使电容量增大的系数等于该材料的介电常数。

但是，在微带线中，一些电力线穿过空气，另一些穿过叠层介质，由于信号路径和返回路径之间介质材料的缘故，电容量必将增大，但电容量会增大多少呢?

空气和部分填充介质的组合就产生了“有效介电常数”。与填充材料后的电容量与以空气为介质时电容量的比值类似，有效介电常数也是导体之间填充材料(无论材料如何分布)后的电容量与导体之间及其周围仅有空气时电容量的比值。

为了计算有效介电常数,首先要计算导体周围为空气时的单位长度电容,然后在导体周围按实际分布情况填充电介质，并计算此时导体之间的单位长度电容,有效介电常数为

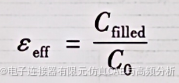
其中，表示导体周围为空气时的电容，表示实际电介质分布时的电容，表示有效介电常数。

使用二维场求解器可准确地计算出这两种情况下的电容，这一工具也是准确计算传输线有效介电常数的唯一方法。下文将会讲到，有效介电常数是非常重要的性能参数，因为它直接决定了传输线中的信号速度。

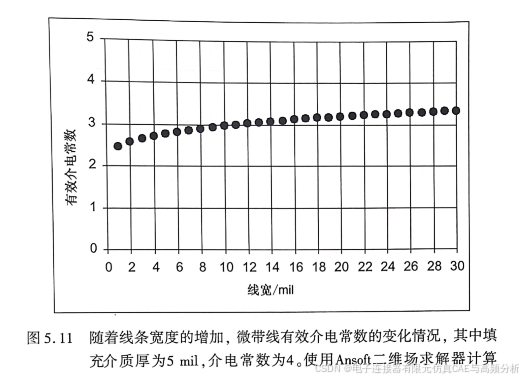
图5.11示意了随线条宽度的增加，微带线的有效介电常数的变化情况。填充介质材料本身的介电常数为4。当线条很宽时，大部分电力线都在介质材料中，这时有效介电常数接近于4。当线条很窄时，大部分电力线在空气中，此时有效介由堂数小于3，这反映了低介电常数空气的影响。

提示： 叠层材料的固有介电常数是不会变化的，只是当导体之间的场穿过不同比例的空气和介质时，才会造成电容的变化。

如果在微带线的顶层加上介质材料，则空气中的边缘电力线穿过的介电常数会增大，微带线的电容也会增加。当微带线上面有介质材料时，称为嵌入微带线。如果仅有一部分电力线穿过介质材料，则称为部分嵌入微带线，例如阻焊涂层。如果所有的电力线都在介质材料中，则称为全嵌入微带线。三种不同嵌入程度的微带线电力线分布如图5.12所示。

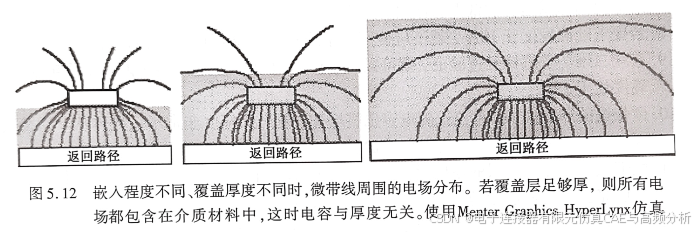
为了覆盖住全部电力线，以使有效介电常数等于介质介电常数，需要在微带线上加多厚的材料呢?用二维场求解器很容易就能解决这个问题。图5.13给出了在微带线顶层增加相同介电常数(为4)叠层材料时的单位长度电容，其中介质厚度为5 mil,线宽为10 mil。

在这个示例中，完全覆盖住边缘场时，线条顶层的介质厚度约等于线宽。

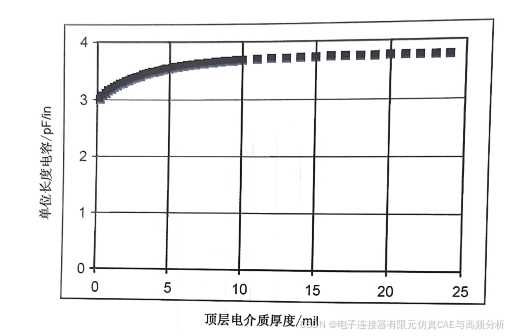
图5.13顶层电介质厚度增加时，微带线单位长度电容的变化情况。使用Ansoft二维场求解器计算。

有效介电常数: