旅游完回来继续学习。

先来看一下图论的理论部分，然后稍微做一下DFS的题目。

图的基本概念

二维坐标中，两点可以连成线，多个点连成的线就构成了图。

当然图也可以就一个节点，甚至没有节点（空图）

图的种类

整体上一般分为 有向图 和 无向图。

有向图是指 图中边是有方向的：

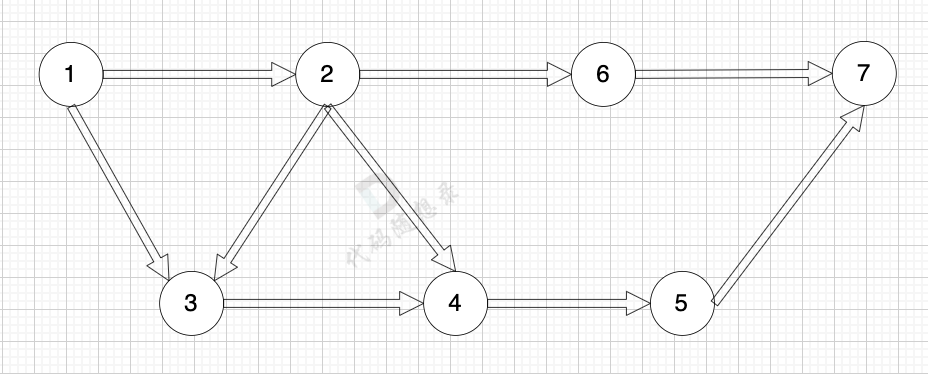
无向图是指 图中边没有方向：

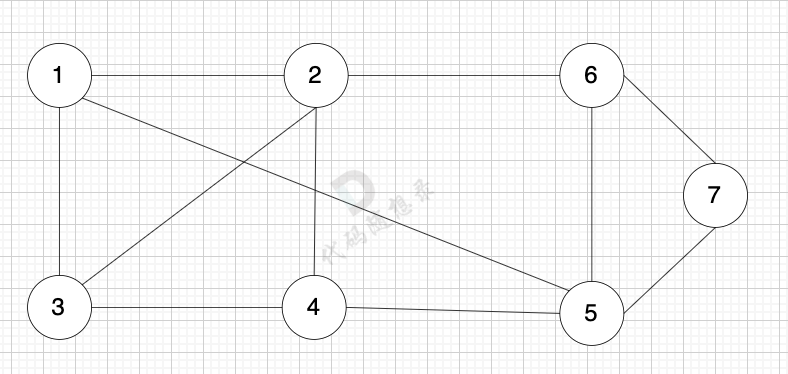
加权有向图，就是图中边是有权值的，例如：

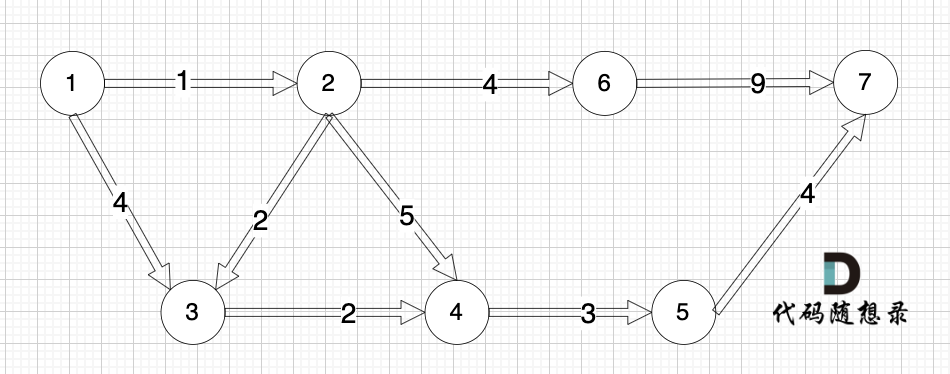
加权无向图也是同理。

度

无向图中有几条边连接该节点，该节点就有几度。

例如，该无向图中，节点4的度为5，节点6的度为3。

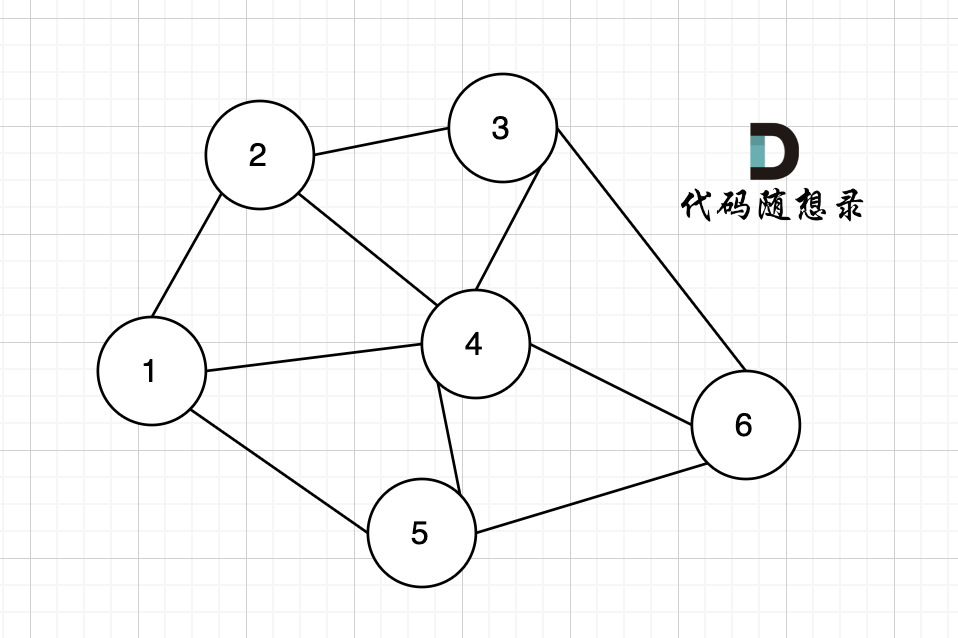
在有向图中，每个节点有出度和入度。

出度：从该节点出发的边的个数。

入度：指向该节点边的个数。

例如，该有向图中，节点3的入度为2，出度为1，节点1的入度为0，出度为2。

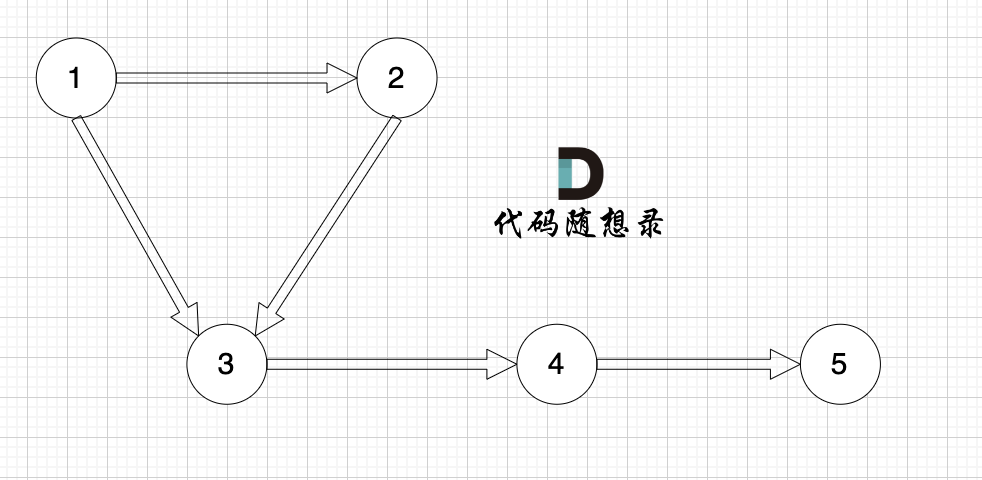
连通性

在图中表示节点的连通情况，我们称之为连通性。

连通图

在无向图中，任何两个节点都是可以到达的，我们称之为连通图 ，如图：

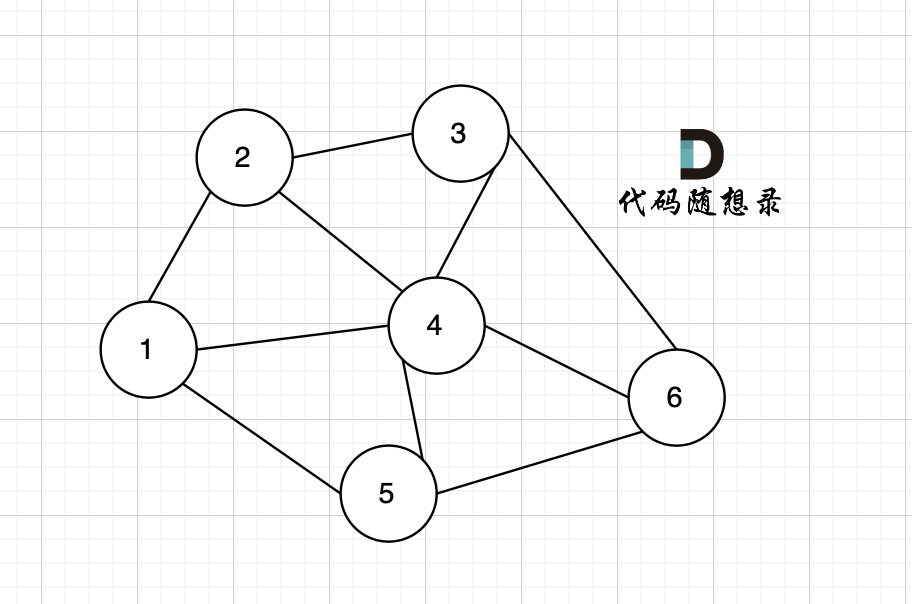
如果有节点不能到达其他节点，则为非连通图，如图：

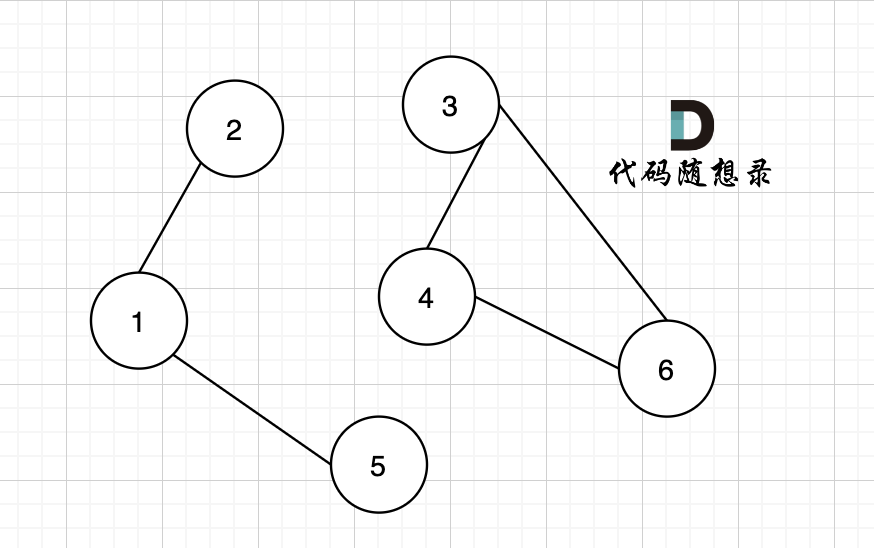
节点1 不能到达节点4。

强连通图

在有向图中，任何两个节点是可以相互到达的，我们称之为 强连通图。

这里有录友可能想，这和无向图中的连通图有什么区别，不是一样的吗？

我们来看这个有向图：

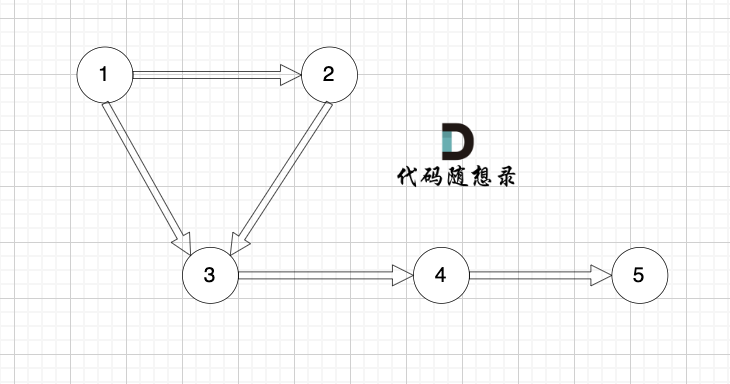
这个图是强连通图吗？

初步一看，好像这节点都连着，但这不是强连通图，节点1可以到节点5，但节点5不能到节点1 。

强连通图是在有向图中任何两个节点是可以相互到达

下面这个有向图才是强连通图：

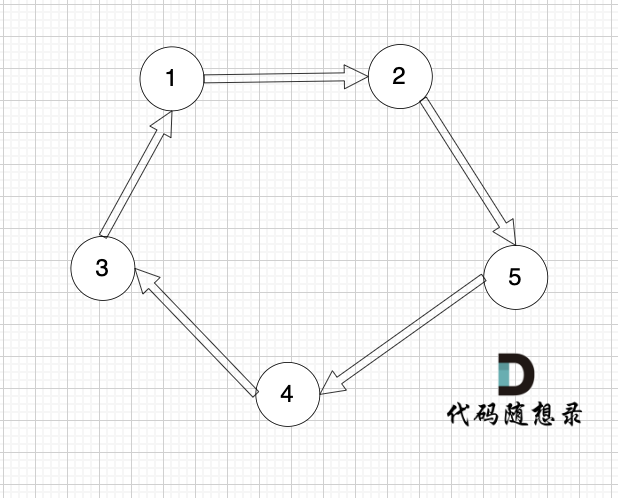
连通分量

在无向图中的极大连通子图称之为该图的一个连通分量。

只看概念大家可能不理解，我来画个图：

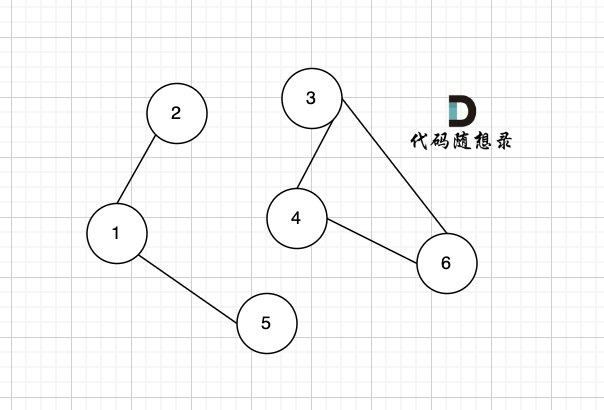
该无向图中 节点1、节点2、节点5 构成的子图就是 该无向图中的一个连通分量，该子图所有节点都是相互可达到的。

同理，节点3、节点4、节点6 构成的子图 也是该无向图中的一个连通分量。

那么无向图中 节点3 、节点4 构成的子图 是该无向图的联通分量吗？

不是！

因为必须是极大联通子图才能是连通分量，所以 必须是节点3、节点4、节点6 构成的子图才是连通分量。

在图论中，连通分量是一个很重要的概念，例如岛屿问题（后面章节会有专门讲解）其实就是求连通分量。

强连通分量

在有向图中极大强连通子图称之为该图的强连通分量。

如图：

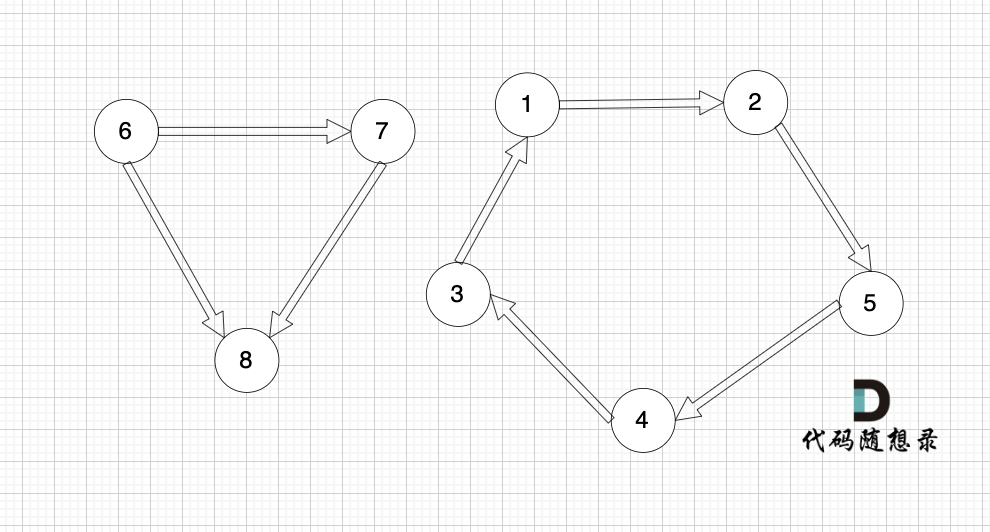
节点1、节点2、节点3、节点4、节点5 构成的子图是强连通分量，因为这是强连通图，也是极大图。

节点6、节点7、节点8 构成的子图 不是强连通分量，因为这不是强连通图，节点8 不能达到节点6。

节点1、节点2、节点5 构成的子图 也不是 强连通分量，因为这不是极大图。

图的构造

我们如何用代码来表示一个图呢？

一般使用邻接表、邻接矩阵 或者用类来表示。

主要是 朴素存储、邻接表和邻接矩阵。

关于朴素存储，这是我自创的名字，因为这种存储方式，就是将所有边存下来。

例如图：

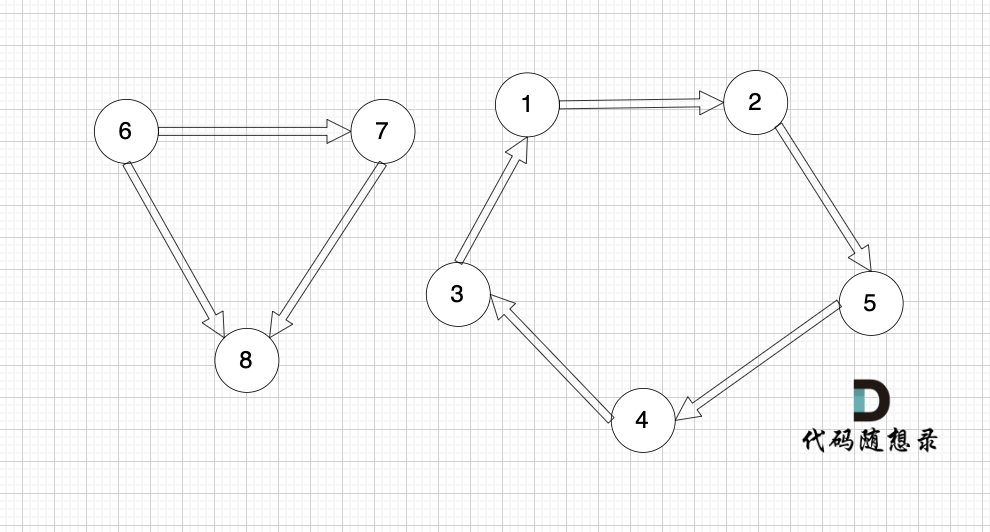
图中有8条边，我们就定义 8 * 2的数组，即有n条边就申请n * 2，这么大的数组：

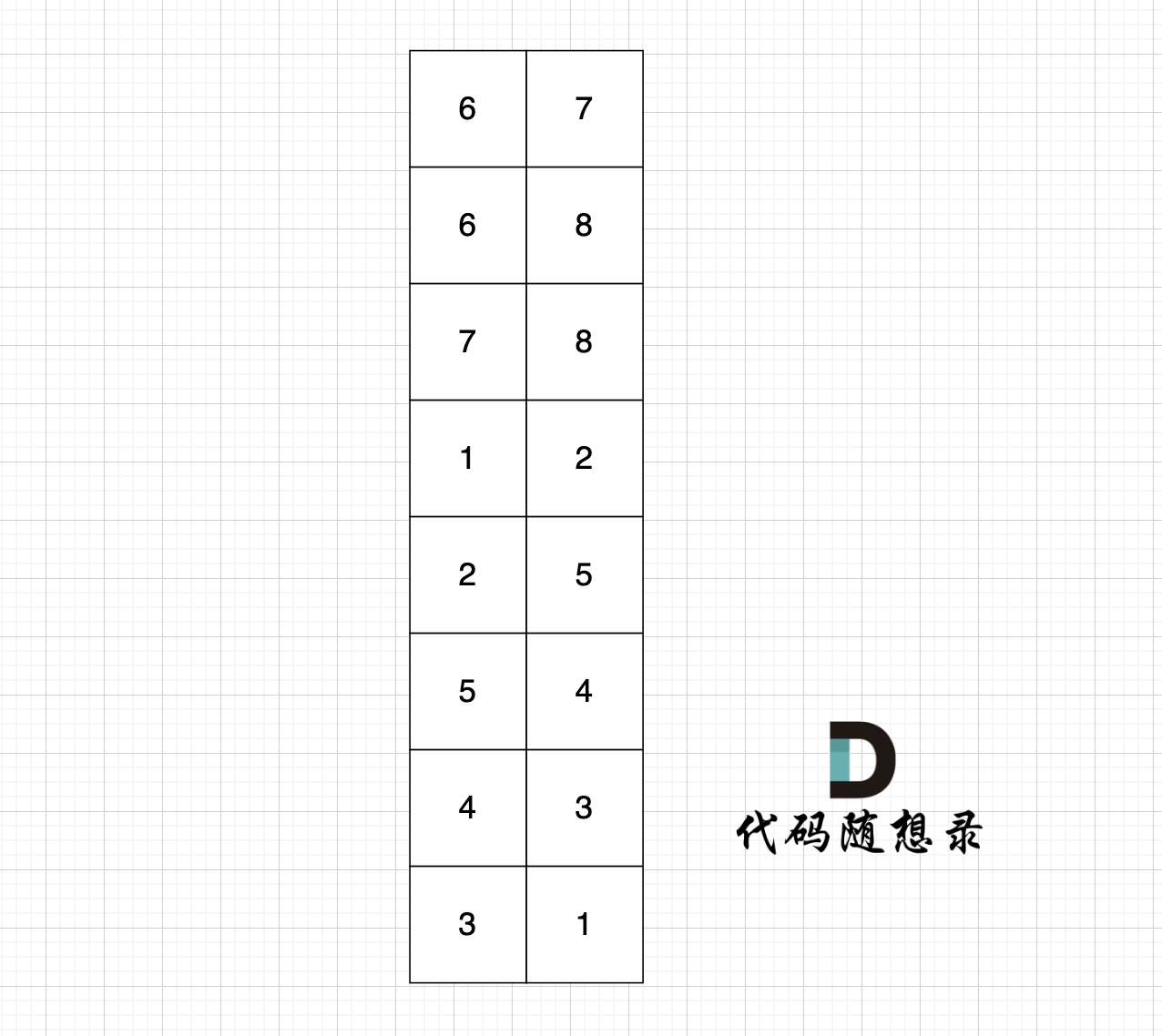
数组第一行：6 7，就表示节点6 指向 节点7，以此类推。

当然可以不用数组，用map，或者用 类 到可以表示出 这种边的关系。

这种表示方式的好处就是直观，把节点与节点之间关系很容易展现出来。

但如果我们想知道 节点1 和 节点6 是否相连，我们就需要把存储空间都枚举一遍才行。

这是明显的缺点，同时，我们在深搜和广搜的时候，都不会使用这种存储方式。

因为 搜索中，需要知道 节点与其他节点的链接情况，而这种朴素存储，都需要全部枚举才知道链接情况。

在图论章节的后面文章讲解中，我会举例说明的。大家先有个印象。

邻接矩阵

邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图，有多少节点就申请多大的二维数组。

例如： grid[2][5] = 6，表示 节点 2 连接 节点5 为有向图，节点2 指向 节点5，边的权值为6。

如果想表示无向图，即：grid[2][5] = 6，grid[5][2] = 6，表示节点2 与 节点5 相互连通，权值为6。

如图：

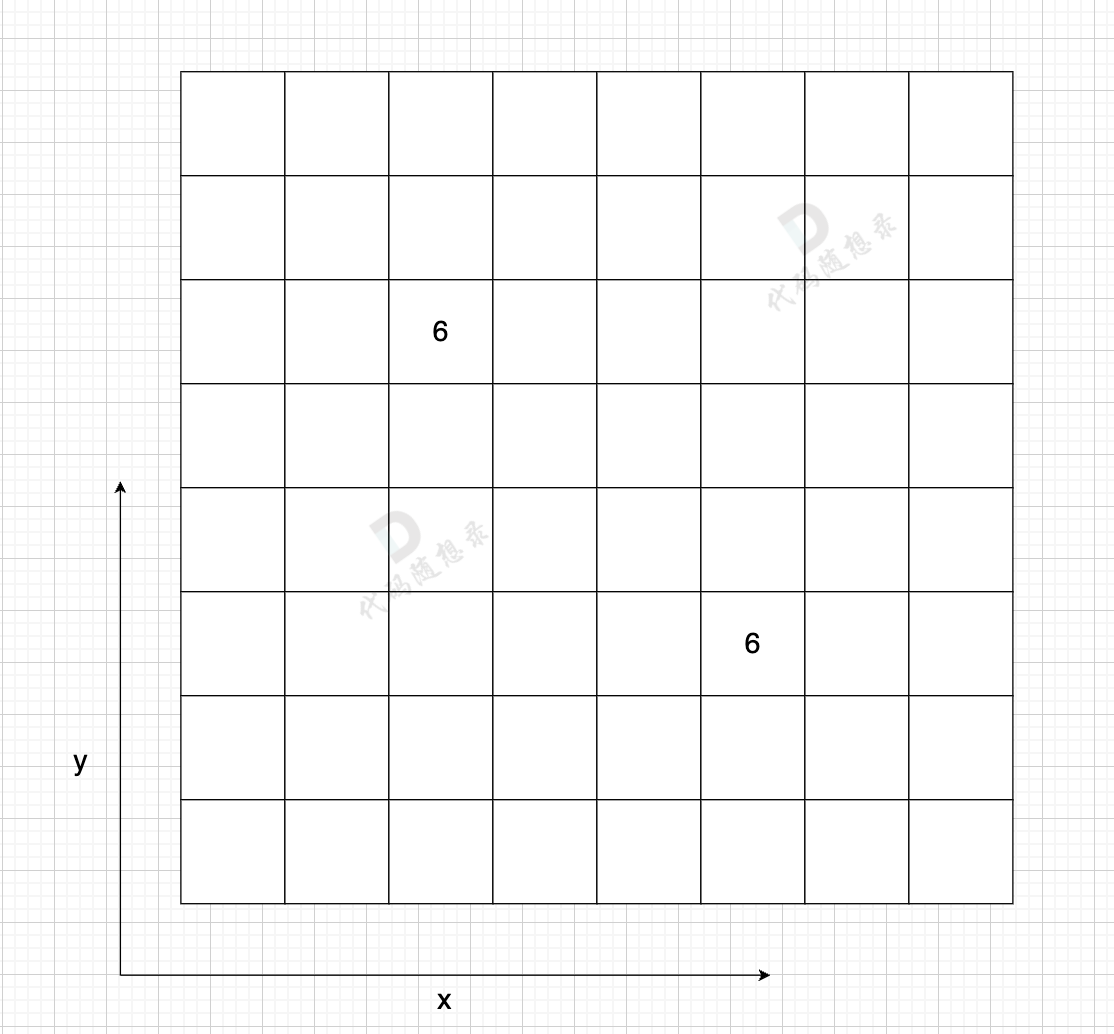
在一个 n （节点数）为8 的图中，就需要申请 8 * 8 这么大的空间。

图中有一条双向边，即：grid[2][5] = 6，grid[5][2] = 6

这种表达方式（邻接矩阵） 在 边少，节点多的情况下，会导致申请过大的二维数组，造成空间浪费。

而且在寻找节点连接情况的时候，需要遍历整个矩阵，即 n * n 的时间复杂度，同样造成时间浪费。

邻接矩阵的优点：

• 表达方式简单，易于理解
• 检查任意两个顶点间是否存在边的操作非常快
• 适合稠密图，在边数接近顶点数平方的图中，邻接矩阵是一种空间效率较高的表示方法。

缺点：

• 遇到稀疏图，会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵，造成时间浪费

邻接表

邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图，有多少边 才会申请对应大小的链表。

邻接表的构造如图：

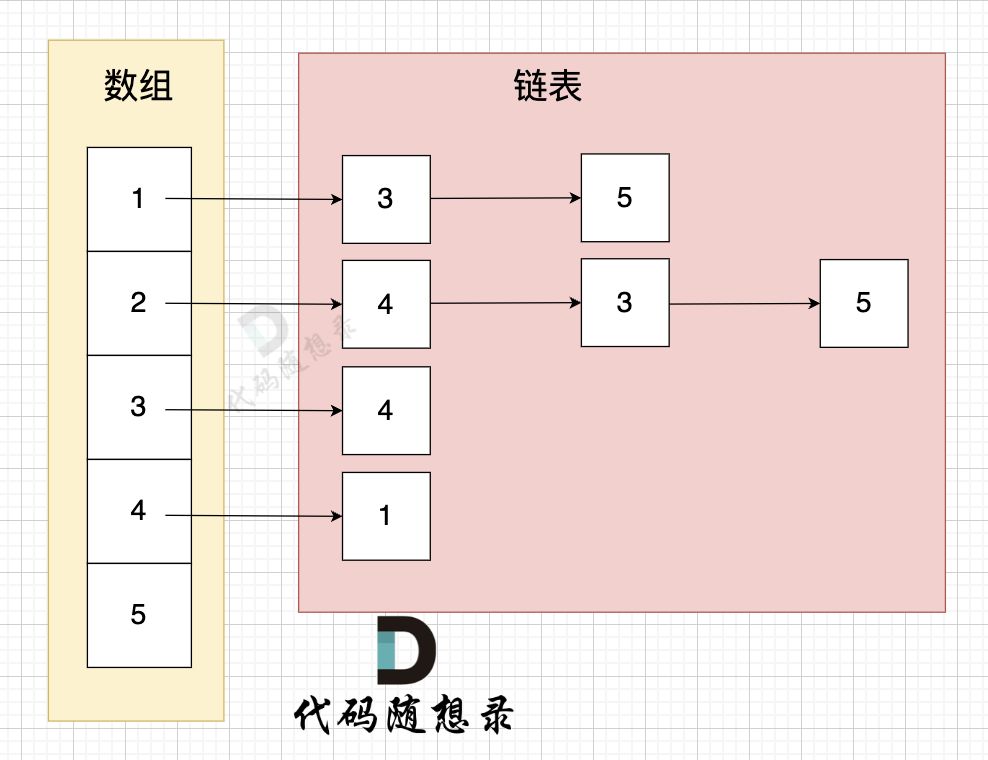
这里表达的图是：

• 节点1 指向 节点3 和 节点5
• 节点2 指向 节点4、节点3、节点5
• 节点3 指向 节点4
• 节点4指向节点1

有多少边 邻接表才会申请多少个对应的链表节点。

从图中可以直观看出 使用 数组 + 链表 来表达 边的连接情况 。

邻接表的优点：

• 对于稀疏图的存储，只需要存储边，空间利用率高
• 遍历节点连接情况相对容易

缺点：

• 检查任意两个节点间是否存在边，效率相对低，需要 O(V)时间，V表示某节点连接其他节点的数量。
• 实现相对复杂，不易理解

以上大家可能理解比较模糊，没关系，因为大家还没做过图论的题目，对于图的表达没有概念。

这里我先不给出具体的实现代码，大家先有个初步印象，在后面算法题实战中，我还会讲到具体代码实现，等带大家做算法题，写了代码之后，自然就理解了。

图的遍历方式

图的遍历方式基本是两大类：

• 深度优先搜索（dfs）
• 广度优先搜索（bfs）

二叉树的递归遍历，是dfs 在二叉树上的遍历方式。

二叉树的层序遍历，是bfs 在二叉树上的遍历方式。

dfs 和 bfs 一种搜索算法，可以在不同的数据结构上进行搜索，在二叉树章节里是在二叉树这样的数据结构上搜索。

而在图论章节，则是在图（邻接表或邻接矩阵）上进行搜索。

然后来看一道题目：98. 所有可达路径

这道题需要找出所有的路径，很明显是一道深搜的题目。

而对于深搜的题目来讲，最重要的就是搞清楚递归的参数，条件，终止情况

但是，由于这里是ACM模式，所以我们还需要注意数据的读取和存储，其实这道题存储量不大，三种图的存储方式都是可以的。但是写法也会发生变化，下面把三种方式都放出来。

邻接矩阵写法

#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 1节点到终点的路径void dfs (const vector<vector<int>>& graph, int x, int n) {// 当前遍历的节点x 到达节点n if (x == n) { // 找到符合条件的一条路径result.push_back(path);return;}for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点if (graph[x][i] == 1) { // 找到 x链接的节点path.push_back(i); // 遍历到的节点加入到路径中来dfs(graph, i, n); // 进入下一层递归path.pop_back(); // 回溯，撤销本节点}}
}int main() {int n, m, s, t;cin >> n >> m;// 节点编号从1到n，所以申请 n+1 这么大的数组vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));while (m--) {cin >> s >> t;// 使用邻接矩阵 表示无线图，1 表示 s 与 t 是相连的graph[s][t] = 1;}path.push_back(1); // 无论什么路径已经是从0节点出发dfs(graph, 1, n); // 开始遍历// 输出结果if (result.size() == 0) cout << -1 << endl;for (const vector<int> &pa : result) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

邻接表写法

#include <iostream>
#include <vector>
#include <list>
using namespace std;vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 1节点到终点的路径void dfs (const vector<list<int>>& graph, int x, int n) {if (x == n) { // 找到符合条件的一条路径result.push_back(path);return;}for (int i : graph[x]) { // 找到 x指向的节点path.push_back(i); // 遍历到的节点加入到路径中来dfs(graph, i, n); // 进入下一层递归path.pop_back(); // 回溯，撤销本节点}
}int main() {int n, m, s, t;cin >> n >> m;// 节点编号从1到n，所以申请 n+1 这么大的数组vector<list<int>> graph(n + 1); // 邻接表while (m--) {cin >> s >> t;// 使用邻接表 ，表示 s -> t 是相连的graph[s].push_back(t);}path.push_back(1); // 无论什么路径已经是从0节点出发dfs(graph, 1, n); // 开始遍历// 输出结果if (result.size() == 0) cout << -1 << endl;for (const vector<int> &pa : result) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

下面是笔者自己写的朴素存储的方式：

#include<iostream>
#include<vector>
using namespace std;vector<vector<int>> path;
vector<int> pre_path;void dfs(vector<pair<int,int>> ab,int i,int n){if(i==n){path.push_back(pre_path);return;}for(auto pre:ab){int k=0;if(pre.first==i)    k=pre.second;pre_path.push_back(k);dfs(ab,k,n);pre_path.pop_back();}
}int main(){int n,m=0;cin>>n>>m;vector<pair<int,int>>   ab(m,{0,0});for(int i=0;i<m;i++){cin>>ab[i].first>>ab[i].second;}pre_path.push_back(1);dfs(ab,1,n);if (path.size() == 0) cout << -1 << endl;for (const vector<int> &pa : path) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

OK，今天就到这