假设检验的原理

假设检验是统计学中用于判断样本数据是否支持某个特定假设的方法。其核心思想是通过样本数据对总体参数或分布提出假设，并利用统计量来判断这些假设的合理性。假设检验的基本步骤如下：

1. 假设（Hypothesis）

在统计学中，假设是指对总体参数（如均值、方差、比例等）或数据分布的一种猜测或主张。

例如：

“某新药比旧药更有效”（即新药组的均值疗效 > 旧药组的均值疗效）。
“男性和女性的工资水平无差异”（即两组的工资均值相等）。

假设通常分为：

原假设（Null Hypothesis, H₀）：默认成立的假设，通常表示“无效果”、“无差异”或“无关系”。

例如：H₀: μ = 100（总体均值等于100）。

备择假设（Alternative Hypothesis, H₁）：与原假设对立，表示“有效果”、“有差异”或“有关系”。

例如：H₁: μ ≠ 100（双侧检验）、H₁: μ > 100（单侧右尾检验）、H₁: μ < 100（单侧左尾检验）。

2. 假设检验（Hypothesis Testing）

假设检验是一种统计方法，用于判断样本数据是否支持原假设，或者是否有足够证据拒绝原假设而支持备择假设。

核心思想：
- 先假设 H₀ 为真，然后计算在当前假设下观察到样本数据的概率（P值）。
- 如果这个概率很小（通常 ≤ 0.05），则拒绝 H₀，认为 H₁ 更可信。

如何提出假设？

提出假设是假设检验的第一步，需要结合研究问题和数据特性。以下是具体方法：

1. 明确研究问题

先确定你要验证的核心问题。例如：

“新教学方法是否提高了学生成绩？”
“A品牌电池的续航时间是否比B品牌长？”
“吸烟是否与肺癌发病率相关？”

2. 确定检验类型

参数检验（适用于已知分布的总体参数，如均值、方差）：

例如：t检验（均值）、Z检验（比例）、F检验（方差）等。

非参数检验（适用于未知分布或非数值数据）：

例如：Mann-Whitney U检验（比较两组中位数）、卡方检验（分类变量独立性）等。

3. 设定原假设（H₀）和备择假设（H₁）

H₀ 通常是“无差异”或“无影响”的保守假设，例如：

“新旧教学方法无差异”（H₀: μ₁ = μ₂）。
“A品牌和B品牌电池续航时间相同”（H₀: μ_A = μ_B）。

H₁ 取决于研究目标，可以是：

双侧检验（Two-tailed）：只关心“是否有差异”，不关心方向。

例如：H₁: μ₁ ≠ μ₂

单侧检验（One-tailed）：关心“是否更大/更小”。

例如：H₁: μ₁ > μ₂（新方法更好）或 H₁: μ_A < μ_B（A品牌更差）

4. 选择显著性水平（α）

通常 α = 0.05（5%），表示允许犯第一类错误（错误拒绝H₀）的概率为5%。
如果研究要求更严格（如医学试验），可以选 α = 0.01。

举例说明

例1：检验新药是否比旧药更有效

假设：

H₀: μ_新 ≤ μ_旧（新药不比旧药更好）
H₁: μ_新 > μ_旧（新药更有效，单侧右尾检验）

检验方法：独立样本 t 检验（比较两组均值）。

例2：检验某班级的平均成绩是否为75分

研究问题：班级平均分是否 ≠ 75？

假设：
- H₀: μ = 75（班级平均分等于75）
- H₁: μ ≠ 75（班级平均分不等于75，双侧检验）

检验方法：单样本 t 检验。

例3：检验性别是否影响工资水平

研究问题：男女工资均值是否不同？

假设：
- H₀: μ_男 = μ_女（性别不影响工资）
- H₁: μ_男 ≠ μ_女（性别影响工资，双侧检验）

检验方法：独立样本 t 检验或 Mann-Whitney U 检验（若数据非正态）。

总结

假设是对总体参数的猜测，分为原假设（H₀）和备择假设（H₁）。
假设检验是通过统计方法判断是否拒绝H₀。
如何提出假设：
- 明确研究问题 → 选择检验类型 → 设定H₀和H₁ → 选择α。
关键点：
- H₀通常是“无差异”的保守假设。
- H₁可以是双侧（≠）或单侧（> 或 <）。
- α通常取0.05，但可根据研究调整。

至于什么是单侧检验什么是双侧检验呢?

假设检验的方向性决定了你是用单侧检验（One-tailed Test）还是双侧检验（Two-tailed Test）。它们的核心区别在于：

比较项	单侧检验	双侧检验
研究问题	只关心“是否更大”或“是否更小”	只关心“是否有差异”（不关心方向）
备择假设（H₁）	H₁: μ > μ₀（右尾）或 μ < μ₀（左尾）	H₁: μ ≠ μ₀
拒绝域	仅分布在统计量的一侧（左或右）	分布在统计量的两侧（左和右）
适用场景	有明确方向性的预测（如“新药更好”）	无方向性，只检验差异（如“新旧药不同”）

1. 双侧检验（Two-tailed Test）

核心思想：只关心“有没有差异”，不关心是“正差异”还是“负差异”。

备择假设（H₁）：μ ≠ μ₀（可以是更大或更小）。

拒绝域：分布在统计量的左右两侧（例如，|Z| > 1.96）。

举例：

问题：某工厂生产的零件长度标准是10cm，现在怀疑机器有问题，但不确定是偏长还是偏短。

假设：

假设：
- H₀: μ = 10cm（机器正常）
- H₁: μ ≠ 10cm（机器异常，可能偏长或偏短）
检验方法：计算样本均值，如果显著大于或小于10cm，都拒绝H₀。

2. 单侧检验（One-tailed Test）

核心思想：明确关心“是否更大”或“是否更小”。

拒绝域：仅分布在统计量的一侧（例如，Z > 1.645 或 Z < -1.645）。

举例：
- 问题1（右尾）：某新药声称比旧药更有效，需验证是否真的“更有效”。
  - H₀: μ_新 ≤ μ_旧
  - H₁: μ_新 > μ_旧
  - 只有新药显著更好时，才拒绝H₀。
- 问题2（左尾）：某减肥广告声称“平均减重≥5kg”，消费者怀疑夸大效果。
  - H₀: μ ≥ 5kg
  - H₁: μ < 5kg
  - 只有实际减重显著小于5kg时，才拒绝H₀。

双侧检验拒绝域：     单侧检验（右尾）拒绝域：／＼                ／|/    \              /  |/      \            /   |
[拒绝域][拒绝域]    [接受域][拒绝域]

如何选择单侧 or 双侧？

用双侧检验的情况：
- 研究问题只是“是否有差异”，无方向性预测。
- 例如：“男女身高是否不同？”（可能男高或女高）。
用单侧检验的情况：
- 研究问题有明确方向（如“新方法更好”“新药更差”）。
- 例如：“新教学方法是否提高了成绩？”（只需检验是否>）。

注意事项

单侧检验更容易显著（因为拒绝域集中在一侧，统计量更容易达标），但必须提前确定方向，不能看到数据后再选方向（否则是学术不端）。
双侧检验更保守（需要更强的证据才能拒绝H₀），适用于探索性研究。

举个例子

问题：某饮料标称容量为500ml，质检部门想检测是否达标。

如果只是怀疑容量可能不准确（可能多或少）：
- 用双侧检验：H₁: μ ≠ 500ml
如果厂商声称“容量≥500ml”，消费者怀疑不足：
- 用单侧（左尾）检验：H₁: μ < 500ml

拒绝域（Rejection Region）和接受域（Acceptance Region）是假设检验中用于判断是否拒绝原假设（H₀）的统计量范围。它们的划分基于显著性水平（α）和统计量的分布。

1. 拒绝域（Rejection Region）

定义：如果检验统计量（如Z值、t值）落在这一区域，就拒绝H₀，认为备择假设（H₁）更可信。

特点：
- 位于统计量分布的极端区域（尾部）。
- 范围由显著性水平（α）决定（如α=0.05时，拒绝域占分布的5%）。

举例：
- 在正态分布中，若α=0.05（双侧检验），拒绝域是Z < -1.96 或 Z > 1.96。

2. 接受域（Acceptance Region）

定义：如果检验统计量落在这一区域，就不拒绝H₀（注意：不是“接受H₀”，而是“没有足够证据拒绝”）。

特点：
- 位于统计量分布的中间区域。
- 范围是1-α（如α=0.05时，接受域占95%）。

举例：
- 在正态分布中，若α=0.05（双侧检验），接受域是 -1.96 ≤ Z ≤ 1.96。

如何确定拒绝域和接受域？

步骤1：明确检验类型（单侧/双侧）

双侧检验（H₁: μ ≠ μ₀）：拒绝域在分布的两侧。
- 例如：α=0.05时，每侧占2.5%（Z=±1.96）。
单侧检验（H₁: μ > μ₀ 或 μ < μ₀）：拒绝域在分布的一侧。
- 例如：α=0.05时，右尾检验的临界值为Z=1.645。

步骤2：根据分布和α查临界值

Z检验（正态分布）：查Z表。
t检验（t分布）：查t表（需考虑自由度）。
其他分布：如χ²分布、F分布等。

步骤3：画出分布图并标记区域

双侧检验示例（α=0.05）：

拒绝域      接受域      拒绝域
Z < -1.96   -1.96 ≤ Z ≤ 1.96   Z > 1.96

单侧右尾检验示例（α=0.05）：

接受域         拒绝域
Z ≤ 1.645      Z > 1.645

实际案例说明

案例1：单样本Z检验（双侧）

问题：检验某批次灯泡寿命均值是否为1000小时（H₀: μ=1000，H₁: μ≠1000，α=0.05）。
步骤：
1. 计算样本均值（如x̄=1020），标准差（σ=50），n=30。
2. 计算Z值：

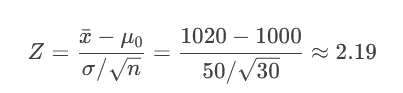
xˉ−μ0=50/30

1020−1000≈2.19
查Z表得临界值：±1.96。
决策：
- Z=2.19 > 1.96 → 落在拒绝域 → 拒绝H₀。

案例2：单侧t检验（左尾）

问题：检验某减肥药平均减重是否<5kg（H₀: μ≥5，H₁: μ<5，α=0.05）。
步骤：
1. 计算样本均值（x̄=4.2），标准差（s=1.2），n=25。
2. 计算t值（自由度=24）：

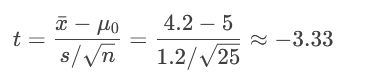
查t表得临界值（左尾）：t=-1.711。
决策：
- t=-3.33 < -1.711 → 落在拒绝域 → 拒绝H₀。

关键注意事项

接受域 ≠ 证明H₀为真：
- 不拒绝H₀只能说明“证据不足”，不能直接得出“H₀正确”的结论。
单侧检验更敏感：
- 同样的α下，单侧检验的临界值更宽松（如Z=1.645 vs 双侧的1.96），更容易拒绝H₀。
P值与拒绝域的关系：
- P值 < α → 检验统计量落在拒绝域内。

总结

拒绝域：统计量的极端值区域，拒绝H₀。
接受域：统计量的中间值区域，不拒绝H₀。
如何确定：
1. 选择单侧/双侧检验。
2. 根据α和分布查临界值。
3. 比较统计量与临界值，判断是否落在拒绝域。

如何用统计量做出决策？

在假设检验中，“用统计量决策”是指通过计算样本数据的统计量（如Z值、t值、F值等），并将其与预先设定的临界值或P值进行比较，从而决定是否拒绝原假设（H₀）。以下是具体步骤和逻辑：

1. 统计量决策的核心逻辑

假设检验的决策基于以下两种等价方法：

临界值法（拒绝域法）：比较统计量与临界值。
P值法：比较P值与显著性水平（α）。

最终结论一致，只是判断方式不同。

2. 统计量决策的步骤

步骤1：计算检验统计量

根据数据类型和假设检验类型，选择合适的统计量公式。例如：

Z检验（总体方差已知或大样本）：

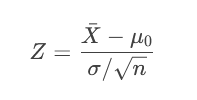
t检验（总体方差未知且小样本）：

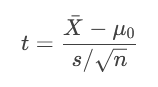
卡方检验（分类数据或方差检验）：

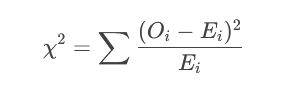
步骤2：确定拒绝域（临界值法）

根据显著性水平（α）和检验类型（单侧/双侧），查统计分布表（Z表、t表等）找到临界值。
- 双侧检验：拒绝域在两侧（如α=0.05时，Z=±1.96）。
- 单侧检验：拒绝域在一侧（如α=0.05右尾检验，Z=1.645）。

决策规则：

如果统计量 > 临界值（或 < -临界值） → 拒绝H₀。

否则 → 不拒绝H₀。

示例（Z检验，双侧α=0.05）

计算得Z=2.1，临界值=±1.96。
2.1 > 1.96 → 拒绝H₀。

步骤3：P值法（更常用的现代方法）

P值是在原假设H₀为真的情况下，观察到当前统计量或更极端值的概率。

P值 ≤ α → 拒绝H₀。
P值 > α → 不拒绝H₀。

如何计算P值？

Z检验：P值 = P(Z ≥ |统计量|) × 2（双侧）或 P(Z ≥ 统计量)（单侧）。
t检验：查t分布表或软件计算。

示例（t检验，单侧α=0.05）

计算得t=2.3，自由度=20，查表得P≈0.016。
0.016 < 0.05 → 拒绝H₀。

3. 实际案例

案例1：Z检验（比较均值）

问题：某工厂生产零件，标准长度μ₀=10cm。质检员抽样30个零件，测得平均长度Xˉ=10.2cmXˉ=10.2cm，总体标准差σ=0.5cm。问零件是否符合标准？（α=0.05）

步骤：

假设：
- H₀: μ = 10cm
- H₁: μ ≠ 10cm（双侧检验）

2.计算Z值：

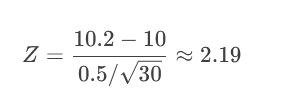
查临界值（α=0.05双侧）：Z=±1.96。
决策：
- 2.19 > 1.96 → 拒绝H₀（零件长度不符合标准）。

P值法：

P(Z ≥ 2.19) ≈ 0.014（单侧），双侧P≈0.028。
0.028 < 0.05 → 拒绝H₀。

案例2：t检验（单侧）

问题：某减肥药声称平均减重≥5kg。消费者协会抽样25人，测得平均减重Xˉ=4.3kgXˉ=4.3kg，样本标准差s=1.2kg。检验广告是否虚假？（α=0.05）

步骤：

假设：
- H₀: μ ≥ 5kg
- H₁: μ < 5kg（左尾检验）

计算t值：

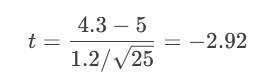
查临界值（α=0.05，自由度=24）：t=-1.711。
决策：
- -2.92 < -1.711 → 拒绝H₀（广告可能虚假）。

P值法：

P(t ≤ -2.92) ≈ 0.004。
0.004 < 0.05 → 拒绝H₀。

4. 总结：统计量决策的核心

计算统计量（Z/t/χ²等）反映样本与H₀的偏离程度。
比较统计量与临界值，或 比较P值与α。
决策：
- 如果统计量落入拒绝域（或P≤α）→ 拒绝H₀。
- 否则 → 不拒绝H₀。

关键点：

临界值法适合手工计算，P值法更精确（软件常用）。
不拒绝H₀ ≠ 证明H₀为真，只是证据不足。
单侧检验更敏感（更容易拒绝H₀），但需提前确定方向。

如何用P值进行假设检验决策？

P值是假设检验中最常用的决策工具之一，它比临界值法更直接，尤其适用于统计软件（如Python、R、SPSS）的分析结果。以下是P值决策的完整步骤和逻辑：

1. P值的定义

P值（P-value）表示：
“在原假设H₀为真的情况下，观察到当前样本数据（或更极端情况）的概率。”
- 如果P值很小（比如≤0.05），说明当前数据在H₀下极不可能发生，因此拒绝H₀。
- 如果P值较大（比如>0.05），说明数据与H₀一致，没有足够证据拒绝H₀。

2. P值决策的步骤

步骤1：设定假设和显著性水平（α）

原假设（H₀）：如 μ = 100
备择假设（H₁）：如 μ ≠ 100（双侧）或 μ > 100（单侧）
显著性水平（α）：通常取 0.05（5%）。

步骤2：计算检验统计量

根据数据类型选择统计量（如Z值、t值、卡方值等）：

Z检验（总体方差已知）：

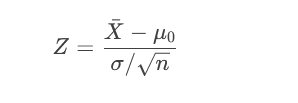
t检验（总体方差未知）：

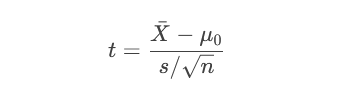
步骤3：计算P值

根据统计量和检验类型计算P值：

双侧检验：P = 2 × P(统计量 ≥ |当前值|)
（例如Z=2.0 → P = 2 × P(Z ≥ 2.0) ≈ 0.0455）
单侧检验：
- 右尾检验：P = P(统计量 ≥ 当前值)
- 左尾检验：P = P(统计量 ≤ 当前值)

注：实际中通常用统计软件（如Python的scipy.stats）直接计算P值，无需手动查表。

步骤4：比较P值与α

如果 P ≤ α → 拒绝H₀，认为结果显著。
如果 P > α → 不拒绝H₀，认为结果不显著。

3. 实际案例

案例1：Z检验（双侧）

问题：某饮料标称容量500ml，质检抽检50瓶，测得平均容量498ml，总体标准差10ml。检验是否达标（α=0.05）。

步骤：

假设：
- H₀: μ = 500ml
- H₁: μ ≠ 500ml（双侧）

2.计算Z值：

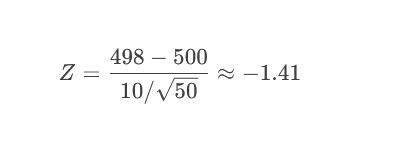
计算P值（双侧）：
- P = 2 × P(Z ≤ -1.41) ≈ 2 × 0.079 = 0.158
决策：
- 0.158 > 0.05 → 不拒绝H₀（容量达标）。

案例2：t检验（单侧左尾）

问题：某减肥药广告称“平均减重≥5kg”，消费者抽检20人，测得平均减重4.2kg，标准差1.5kg。检验广告是否虚假（α=0.05）。

步骤：

假设：
- H₀: μ ≥ 5kg
- H₁: μ < 5kg（左尾）

2.计算t值（自由度=19）：

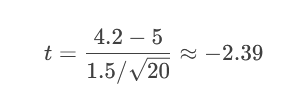
3.计算P值（左尾）：

P = P(t ≤ -2.39) ≈ 0.013

4.决策

0.013 < 0.05 → 拒绝H₀（广告可能虚假）。

4. P值 vs 临界值法

对比项	P值法	临界值法
核心逻辑	直接计算“极端概率”	比较统计量与临界值
适用场景	软件分析、精确计算	手工计算、理论推导
结果一致性	与临界值法结论相同	与P值法结论相同
优势	更直观（直接显示显著性）	适合考试或理论教学

5. 注意事项

P值 ≠ H₀为真的概率：
- P值是基于H₀为真的假设计算的，不能理解为“H₀正确的概率”。
不要混淆单侧/双侧P值：
- 单侧检验的P值通常是双侧的一半（如Z=1.96，单侧P=0.025，双侧P=0.05）。
P值接近α时谨慎结论：
- 如P=0.06（α=0.05），虽不显著，但可能是样本量不足导致的。

6. 总结

P值决策规则：
- P ≤ α → 拒绝H₀（结果显著）。
- P > α → 不拒绝H₀（结果不显著）。
P值的意义：
- 越小越反对H₀，越大越支持H₀的合理性。

P值决策与统计量决策的比较

核心关系：一一对应

首先要理解最根本的一点：对于一个给定的检验，其计算出的统计量（如t值、Z值）都对应着一个唯一的P值。

统计量：是一个绝对数值，表示你的样本数据与H₀的偏离程度（例如，t = 2.5）。偏离程度越大，统计量的绝对值越大。
P值：是一个概率，表示在H₀成立的前提下，出现当前统计量（或更极端情况）的可能性（例如，P = 0.012）。这个可能性越小，P值越小。

它们通过统计分布（如t分布、正态分布）紧密相连。一个较大的统计量绝对值（如 |t| = 2.5）必然对应一个较小的P值（如 P = 0.012）。

对比表格

对比维度	统计量决策（临界值法）	P值决策（P-value法）
决策依据	将计算出的检验统计量（t, Z, F）与临界值（来自分布表）进行比较。	将计算出的P值与显著性水平α（如0.05）进行比较。
决策规则	如果	统计量	>	临界值	，则拒绝H₀。	如果 P值 ≤ α，则拒绝H₀。
决策规则	如果	统计量	>	临界值	（统计量落入拒绝域）	如果 P值 ≤ α，则拒绝H₀。
输出结果	一个数值（如 t = 2.19）	一个概率（如 P = 0.031）
信息量	较少。只知道是否显著，不知道“有多显著”。	更丰富。不仅知道是否显著，还能知道在多大程度上显著（P值越小，拒绝H₀的证据越强）。
直观性	较抽象，需要理解分布和拒绝域的概念。	更直观。P值直接反映了结果的反常程度。
适用场景	手工计算、考试、理论推导。	现代统计分析的主流，几乎所有统计软件（R, Python, SPSS等）默认报告P值。
灵活性	固定。α一旦确定，临界值就固定了。	更灵活。可以直接看到P值是0.049还是0.001，从而判断证据的强度。而临界值法只知道“过了线”。

一个比喻：考试及格线

统计量决策：就像你的考试原始分数是85分（统计量），及格线是60分（临界值）。85 > 60，所以你及格了（拒绝H₀）。但你不知道85分在班里到底处于什么水平。
P值决策：就像告诉你，你的分数超过了97%的同学（P值=0.03）。学校的政策是超过95%的同学算优秀（α=0.05）。因为你超过了97% > 95%，所以你被评为优秀（拒绝H₀）。它不仅告诉了你结果，还告诉了你卓越的程度。

实际案例对比

问题：检验某班级平均分数是否为75分（双侧检验，α=0.05）。

样本数据：n=30, x̄=78, s=10
计算出的统计量：t ≈ 1.64 (自由度df=29)

1. 统计量决策（临界值法）

查t分布表（df=29, α=0.05 双侧），找到临界值 t* = ±2.045。
比较：|1.64| < 2.045
决策：统计量未落入拒绝域，因此不拒绝H₀。

2. P值决策

计算t=1.64对应的P值（使用软件或更精确的表）。对于双侧检验，P值 = 2 * P(T > 1.64) ≈ 0.112。
比较：P值 (0.112) > α (0.05)
决策：不拒绝H₀。

结论

两种方法得出的结论完全相同：没有足够证据拒绝“平均分是75分”的原假设。

但P值提供了更多信息：P=0.112 意味着，即使H₀成立，也有11.2%的概率会观察到这样的样本结果。这个概率远大于5%，所以我们认为这个结果并不反常，不足以推翻H₀。

总结与选择

特性	统计量决策	P值决策	胜出方
结论一致性	完全相同	完全相同	平手
信息丰富度	低	高	P值法
直观性	低	高	P值法
现代应用	少	多（软件标准）	P值法
理论理解	有助于理解分布和拒绝域	更结果导向	统计量法

对于学习者：理解统计量决策有助于夯实假设检验的理论基础，明白决策的整个过程。
对于实践者：P值决策是毫无疑问的首选。它由软件自动计算，提供的信息更丰富，解读更直接。在报告结果时，应同时提供统计量、自由度、P值等信息（例如，t(29) = 1.64, p = .112），而不仅仅是“显著”或“不显著”。

简单来说，P值决策是统计量决策的一种更高级、信息更全面的呈现方式。

怎么表述决策结果——不拒绝而不是接受

为什么是“不拒绝”而不是“接受”？

这背后的核心思想是 “无罪推定” 原则。

原假设（H₀）是默认的“无罪”状态。我们一开始就假定它是成立的，就像法庭上假定被告无罪。
检验的目的是寻找足以推翻这个假设的强有力证据（样本数据），就像检察官寻找能证明被告有罪的证据。
“拒绝H₀”：意味着我们找到了足够强的证据（P值很小），因此我们可以推翻最初的“无罪”设定，判定“有罪”。这是一个积极的、确定的结论。
“不拒绝H₀”：意味着我们找到的证据不足以推翻“无罪”的设定。但这不等于证明了“无罪”。可能的原因有两种：
- H₀确实为真。
- H₀为假，但我们的证据太弱（比如样本太小、数据变异太大），没能检测出来。

“接受”意味着你肯定了H₀的正确性，而假设检验从未证明H₀为真，它只是说明当前数据没有提供反对H₀的证据。

决策	错误（不严谨）的表述	正确（严谨）的表述
拒绝 H₀	“我们接受备择假设H₁。”	“在α=0.05的水平上，有足够的统计证据拒绝原假设H₀。”
	“我们证明了H₁。”	“数据支持备择假设H₁。”
		“结果表明，差异具有统计学意义。”
不拒绝 H₀	“我们接受原假设H₀。”	“在α=0.05的水平上，没有足够的统计证据拒绝原假设H₀。”
	“我们证明了H₀。”	“本次分析未能发现 statistically significant 的证据支持H₁。”
		“数据与原假设H₀一致。”

实际案例中的表述

案例1：拒绝H₀（新药有效性的t检验）

研究问题：新药是否比安慰剂更有效？
H₀: μ_新药 ≤ μ_安慰剂（无效）
H₁: μ_新药 > μ_安慰剂（有效）
结果: t(58) = 2.85, p = 0.003

错误表述：

“我们接受了新药更有效的假设。”

正确表述：

“拒绝原假设。在α=0.05的水平上，统计分析提供了足够的证据（t(58)=2.85, p=0.003）表明新药的治疗效果显著优于安慰剂。”

案例2：不拒绝H₀（零件质量的Z检验）

研究问题：生产线生产的零件长度是否是10cm？
H₀: μ = 10 cm （合格）
H₁: μ ≠ 10 cm （不合格）
结果: Z = 1.20, p = 0.230

错误表述：

“我们得出结论，零件平均长度就是10cm。”

正确表述：

“未能拒绝原假设。在α=0.05的水平上，没有足够的统计证据（Z=1.20, p=0.230）表明零件的平均长度与10cm有统计学上的显著差异。当前数据与生产线运行正常的假设是一致的。”

更进一步的解释（推荐）：

“……未能发现显著差异。但这不能断定零件长度** exactly **是10cm，可能存在的微小差异由于本次样本量有限而未被检测到。建议持续监控或扩大样本量进行进一步验证。”

总结：如何记住并应用

记住法庭比喻：不说“接受无罪”，只说“证据不足，无法定罪”或“证据确凿，认定有罪”。
报告结果时，始终将统计量、P值和决策一起报告。
- 格式：(统计量(自由度)=数值, p=数值)
- 例如：(t(25) = 2.11, p = .045) 或 (χ²(1) = 5.68, p = .017)
使用标准短语：
- 拒绝H₀时：“有足够证据拒绝H₀”、“结果显著”。
- 不拒绝H₀时：“没有足够证据拒绝H₀”、“未发现显著差异”、“数据与H₀一致”。

怎么样表述决策结果——“显著”或“不显著”

核心原则

永远不要只说“显著”或“不显著”：必须说明是在什么显著性水平（α） 下做出的判断。例如，“在0.05水平上显著”。
提供统计证据：必须报告计算出的检验统计量（如 t值、χ²值、F值）和 P值。这是结论的支撑。
区分“统计显著”与“实际显著”：一个结果可能具有统计显著性（即不太可能是偶然发生的），但效应量非常小，在实际业务或科学场景中没有实际意义。
对“不显著”的结果保持谦逊：不说“接受原假设”或“证明没有差异”，而说“未能发现显著差异”或“证据不足以拒绝原假设”。

如何表述“显著”的结果

当 P值 ≤ α 时，我们拒绝原假设（H₀），结果是显著的。

表述结构：结论 + 统计证据 + 上下文含义。

常用话术：

“……之间存在统计学上显著的差异。”
“……对……有显著影响。”
“数据提供了充分的证据表明……”
“我们拒绝原假设，支持……”

举例（假设 α = 0.05）：

T检验： “独立样本t检验显示，使用新教学方法的学生成绩（M=85, SD=4）显著高于使用传统方法的学生（M=80, SD=5），*t*(58) = 3.85, *p* = .002。”
卡方检验： “不同性别与产品偏好之间存在显著关联，χ²(2, N = 200) = 10.52, *p* = .005。”
回归分析： “回归分析表明，每日锻炼时间对减肥效果有显著的正向预测作用，β = .45, *t*(98) = 5.11, *p* < .001。”

如何表述“不显著”的结果

当 P值 > α 时，我们未能拒绝原假设（H₀），结果是不显著的。

表述结构：谨慎结论 + 统计证据 + 可能原因或局限性（可选）。

常用话术：

“……之间的差异无统计学意义。”
“未能发现……对……有显著影响。”
“数据没有提供足够的证据表明……”
“结果不支持备择假设……”
“在本次研究中，……与……没有显著关联。”

举例（假设 α = 0.05）：

T检验： “独立样本t检验发现，A组（M=52, SD=11）与B组（M=55, SD=10）的平均得分差异无统计学意义，*t*(45) = 1.21, *p* = .233。”
更严谨的表述： “……*p* = .233，因此未能拒绝两组均值相等的原假设。该结果可能表明真正差异很小，也可能由于样本量不足导致检验效力（Power）较低，未能检测到存在的差异。”
回归分析： “回归模型显示，受教育年限对起始工资的预测作用不显著，β = .08, *t*(103) = 0.87, *p* = .387。”

表述模板

你可以直接套用以下模板来组织你的语言：

对于“显著”结果：

【统计方法】表明，【自变量/分组变量】对【因变量/结果变量】有【显著/显著的正面/显著的负面】影响/差异（统计量(自由度) = 值, *p* = P值）。具体来说，【用简单语言描述发现，例如：A组的平均值比B组高X个单位】。

对于“不显著”结果：

【统计方法】结果显示，【自变量/分组变量】与【因变量/结果变量】之间未发现显著的关联/差异（统计量(自由度) = 值, *p* = P值）。这意味着当前数据不足以支持【你的研究假设】。

常见错误与陷阱

混淆“统计显著”和“实际重要”：
- 错误：“新的网页设计使点击率显著提升了0.1%（p<0.05），因此我们应该立刻投入百万资金全面推广。”
- 正确：“虽然新设计带来了统计上显著的提升（p<0.05），但0.1%的效应量过小，可能不具备商业价值。建议进行更大规模的测试以评估其实际影响。”
将“不显著”等同于“没有效果”：
- 错误：“我们的实验证明，奖金对员工 productivity 没有影响（p=0.07）。”
- 正确：“在本研究条件下，未能发现奖金对 productivity 有统计上的显著影响（p=0.07）。但p值接近0.05，提示可能存在一个我们因样本量限制而未能捕捉到的真实效应，值得进一步研究。”
忽略报告效应量（Effect Size）：
在报告p值的同时，最好也报告效应量（如Cohen's d, η², R²），这能帮助读者理解显著差异的“幅度”有多大。

总结一下：专业的表述是 “结论 + 统计量 + p值” 的组合。对显著结果，可以自信地解释；对不显著结果，务必保持谨慎，并考虑其可能的原因。这样做才能使你的分析结论显得严谨、可信。

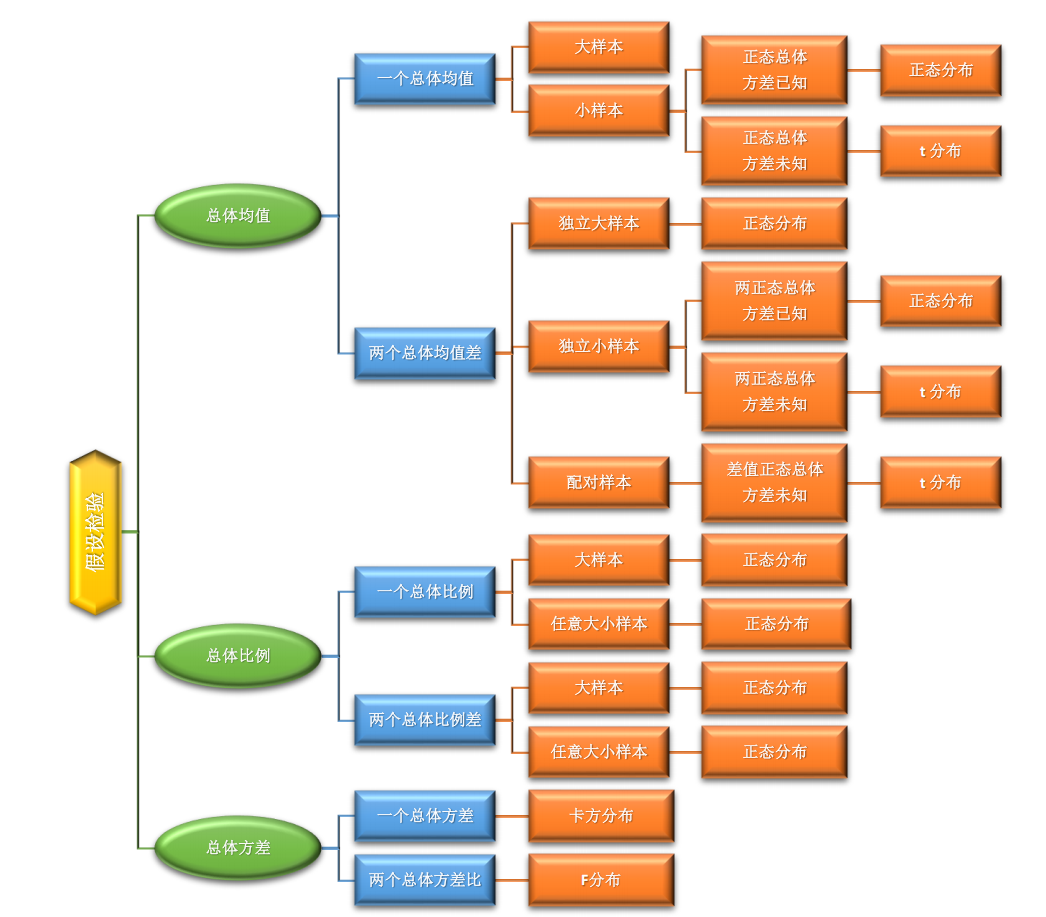
假设检验的7个标准步骤

第1步：提出假设

明确原假设和备择假设。
原假设：
备择假设：

示例：检验一种新减肥药是否有效（已知有效标准是平均减重 > 5kg）。

H₀: μ ≤ 5 kg （新药无效或不比标准好）
H₁: μ > 5 kg （新药有效）

第2步：选择显著性水平

确定第一类错误的概率。
常用选择：。

示例：我们选择 α = 0.05。这意味着我们有5%的风险错误地拒绝一个 actually 为真的H₀（即误判药有效）。

第3步：确定检验统计量及其分布

根据：数据类型、样本量、总体信息。
常见选择：
- ：总体方差已知，或大样本。
- ：总体方差未知，小样本。
- ：检验方差或拟合优度。
- ：比较两个方差。

示例：我们不知道总体方差，且样本量较小（n=25），所以使用 t检验。检验统计量为 t 统计量，服从自由度为 24 的 t 分布。

第4步：制定决策规则

确定拒绝域：根据显著性水平α和备择假设H₁的方向，查相应的分布表，找到临界值。
决策规则：如果检验统计量落在拒绝域，则拒绝H₀。

示例：这是一个右尾检验。查 t 分布表（α=0.05, df=24），得到临界值 **t* = 1.711**。

决策规则：如果计算出的 t > 1.711，就拒绝H₀。

第5步：收集数据并计算检验统计量

从总体中抽取一个随机样本。
根据样本数据计算检验统计量的实际值。

示例：随机抽取25名被试者。计算得样本平均减重 xˉ=5.8xˉ=5.8 kg，样本标准差 s=1.5s=1.5 kg。
计算 t 统计量：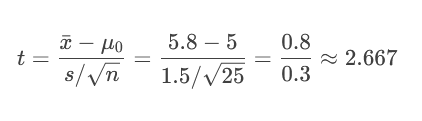

第6步：做出统计决策

将第5步计算出的统计量与第4步制定的决策规则进行比较。
两种等价方法：
1. 临界值法：t = 2.667 > 1.711 → 统计量落入拒绝域。
2. P值法：计算P值（P(t > 2.667) ≈ 0.007）。由于 0.007 < 0.05 (α) → P值小于α。

决策：拒绝原假设H₀。

第7步：给出统计结论

用非技术性语言陈述决策结果，并结合问题背景进行解释。
切记：对“不拒绝H₀”的情况，不要说“接受H₀”。

示例：

统计结论：在0.05的显著性水平上，有足够的统计证据拒绝原假设。
现实意义结论：数据分析表明，该新减肥药的平均减重效果显著高于5kg的标准，具有统计学意义。这意味着我们有足够的信心认为该药是有效的。

真题解读

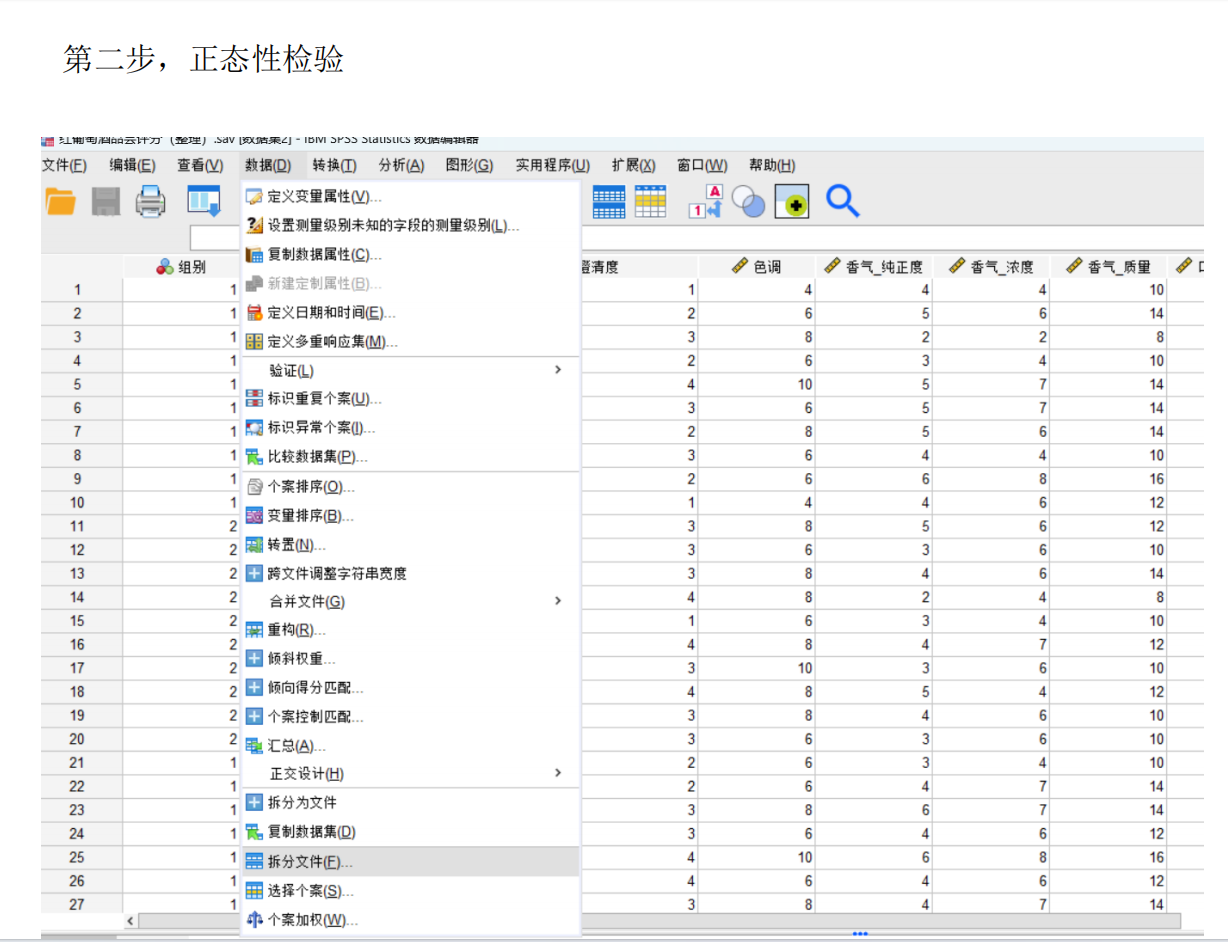
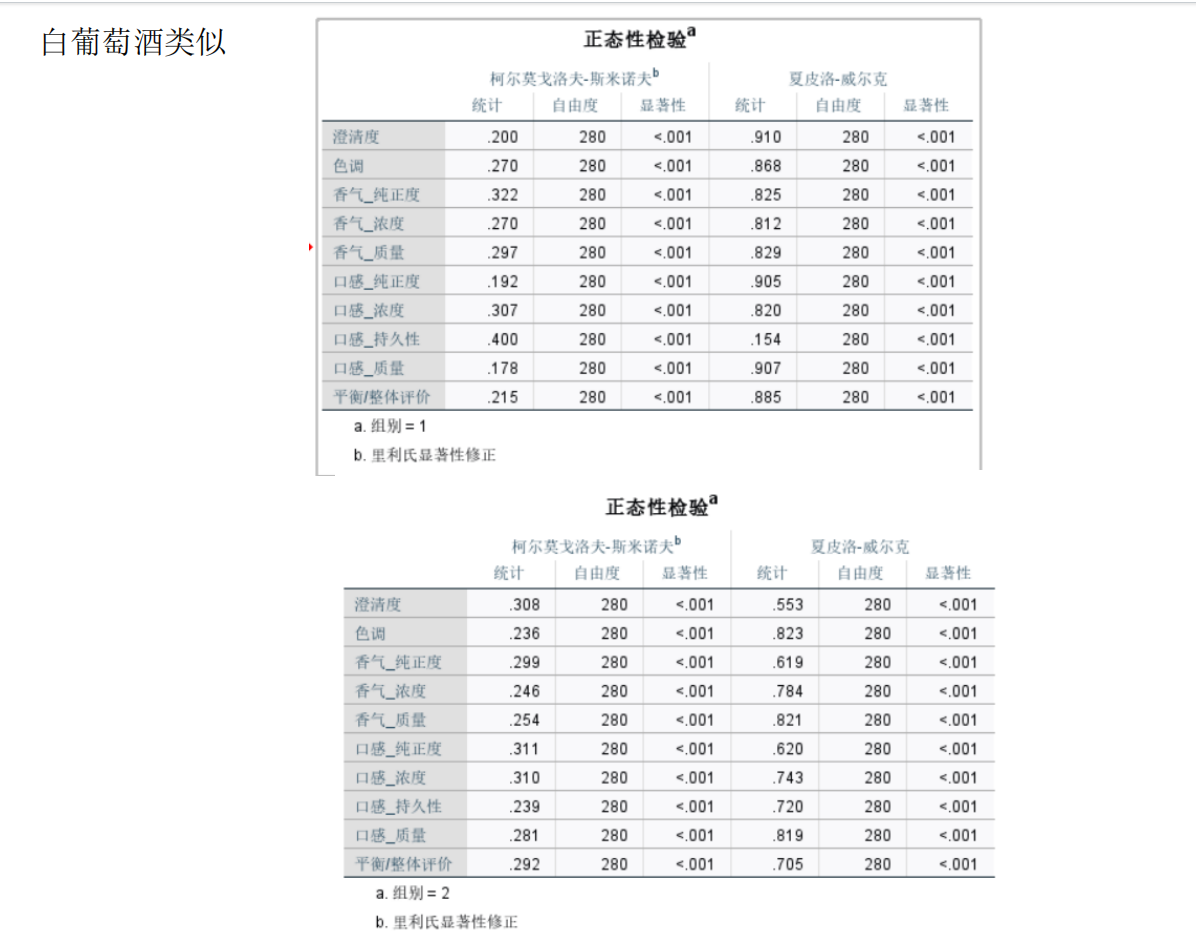
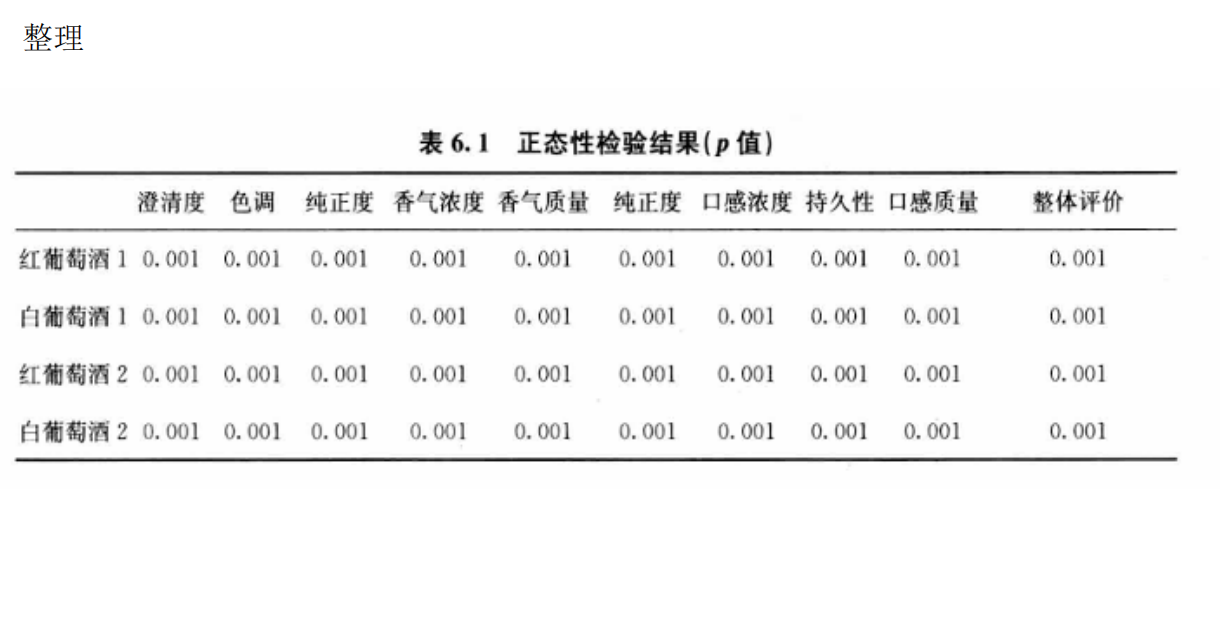
问题1的分析：两组评酒员评价结果的显著性差异及可信度比较

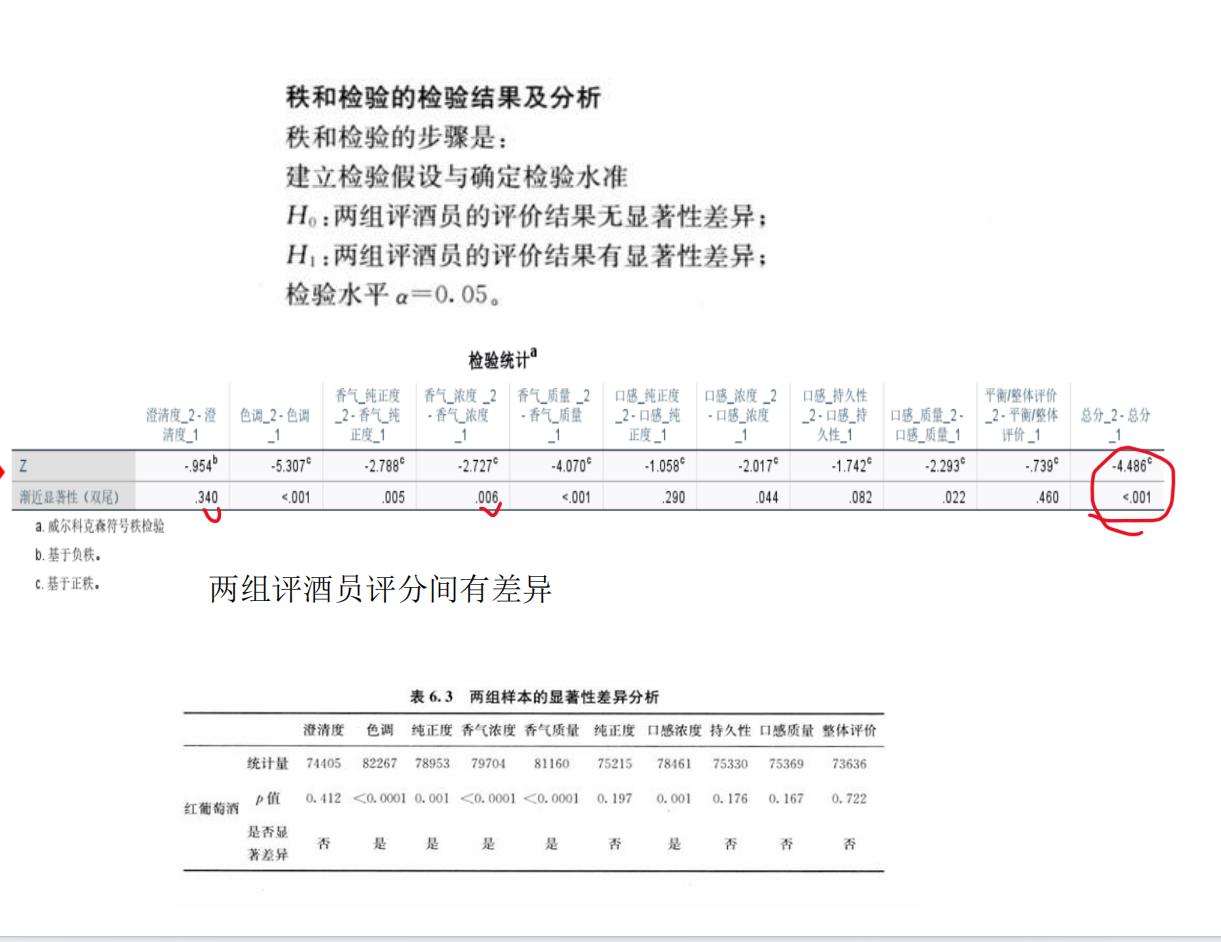
步骤1：提出假设

原假设（H₀）：两组评酒员的评价结果无显著性差异（即两组评分均值相等）。
备择假设（H₁）：两组评酒员的评价结果存在显著性差异（即两组评分均值不相等）。

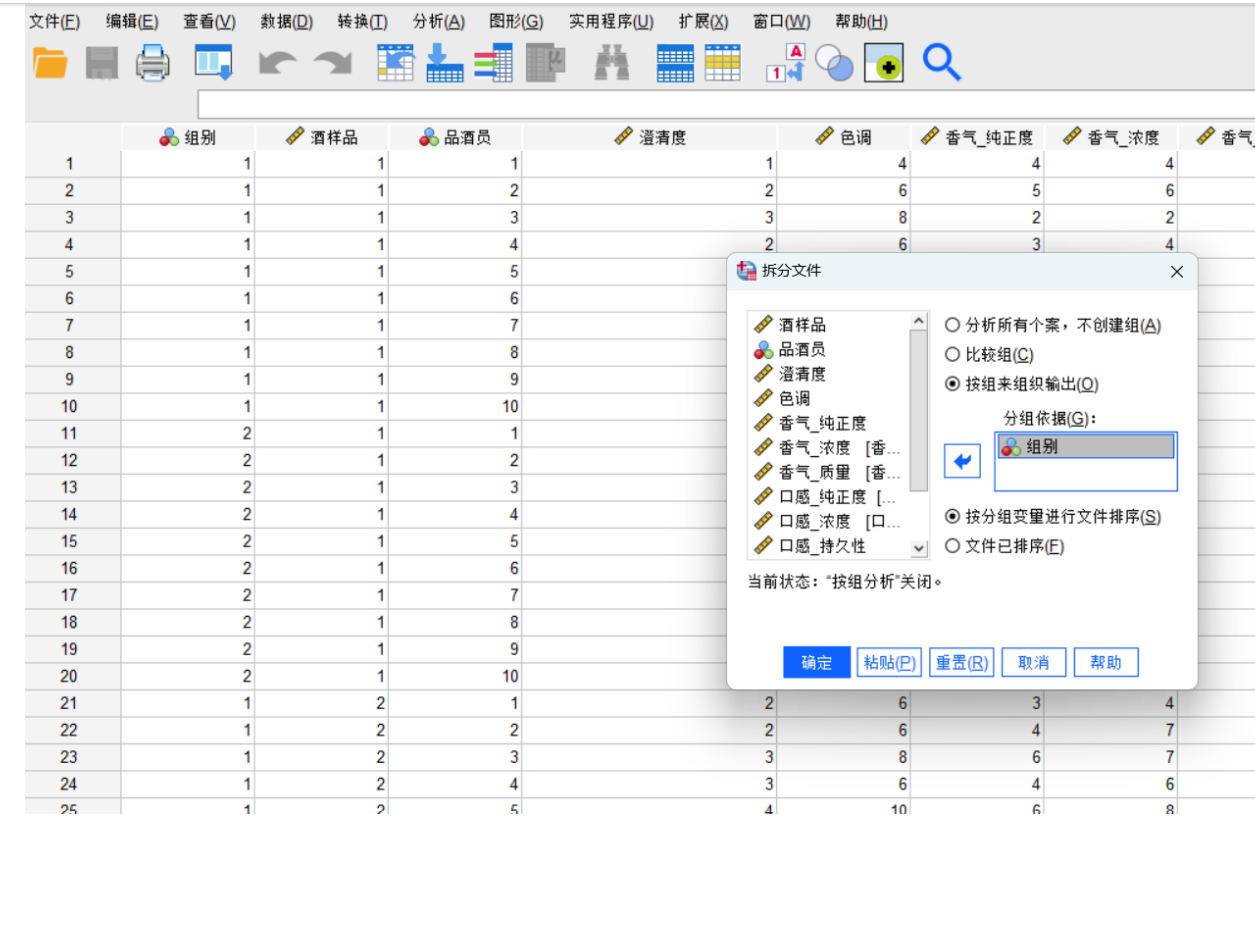
步骤2：选择检验方法

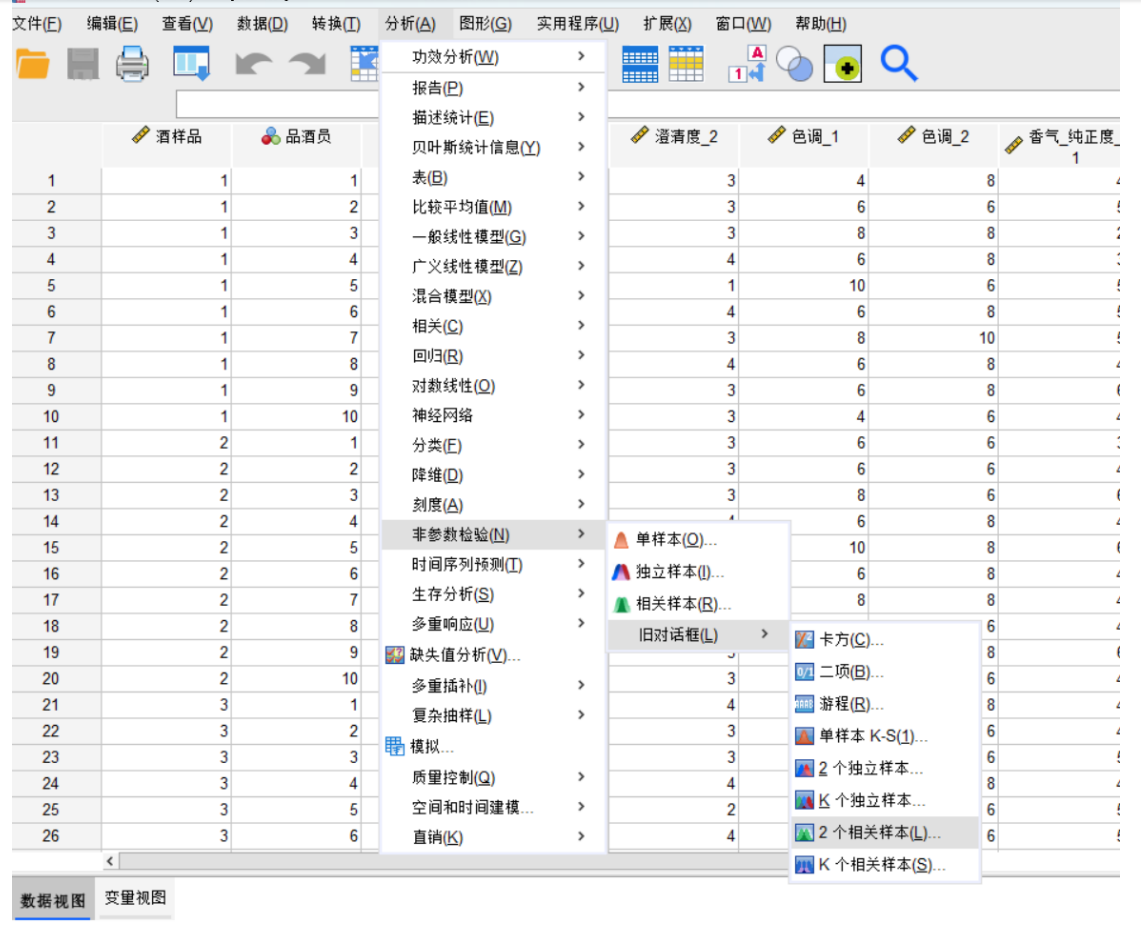
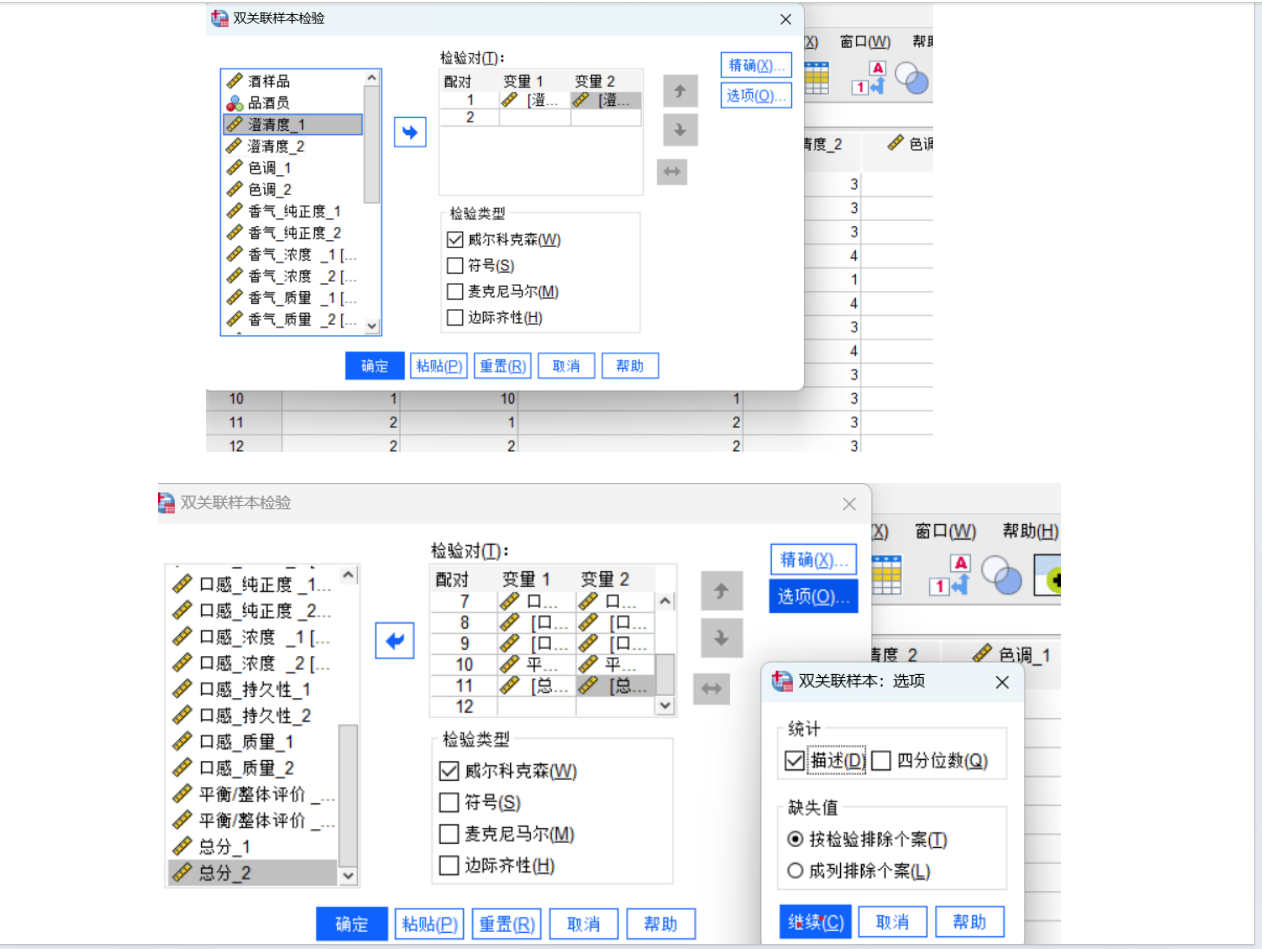
由于附件1中包含两组评酒员（每组多人）对多种葡萄酒的评分数据（连续数值），且需比较两组独立样本的均值差异，我们选择两独立样本t检验（若数据符合正态性和方差齐性）或Mann-Whitney U检验（非参数检验，若数据不满足正态性）。
理由：

每组评酒员对同一样本（葡萄酒）的评分可视为一个组别的整体评价（可计算组内平均分或中位数）。
需要比较两组评分的分布是否相同。

步骤3：确定显著性水平

设定显著性水平α = 0.05（即95%置信水平）。
若p值 < 0.05，则拒绝原假设，认为两组存在显著差异；否则接受原假设。

步骤4：计算检验统计量

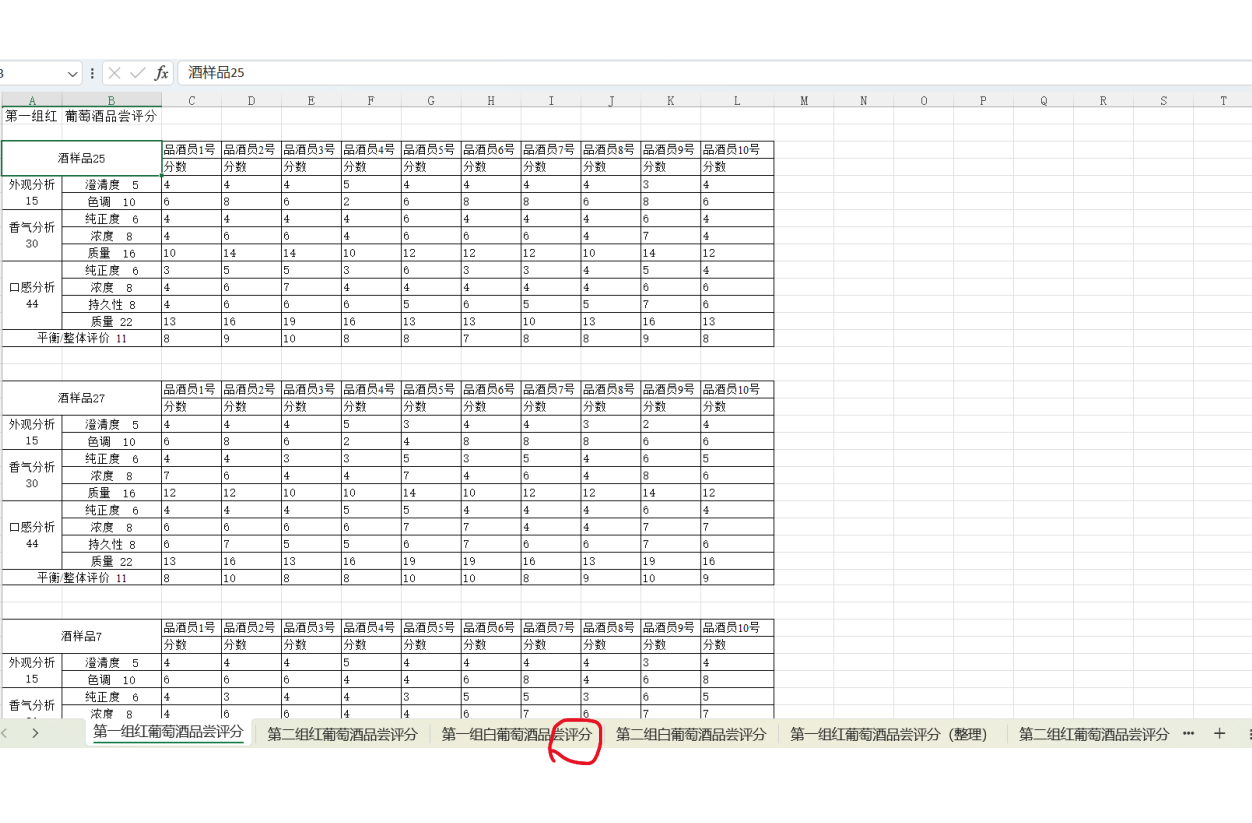
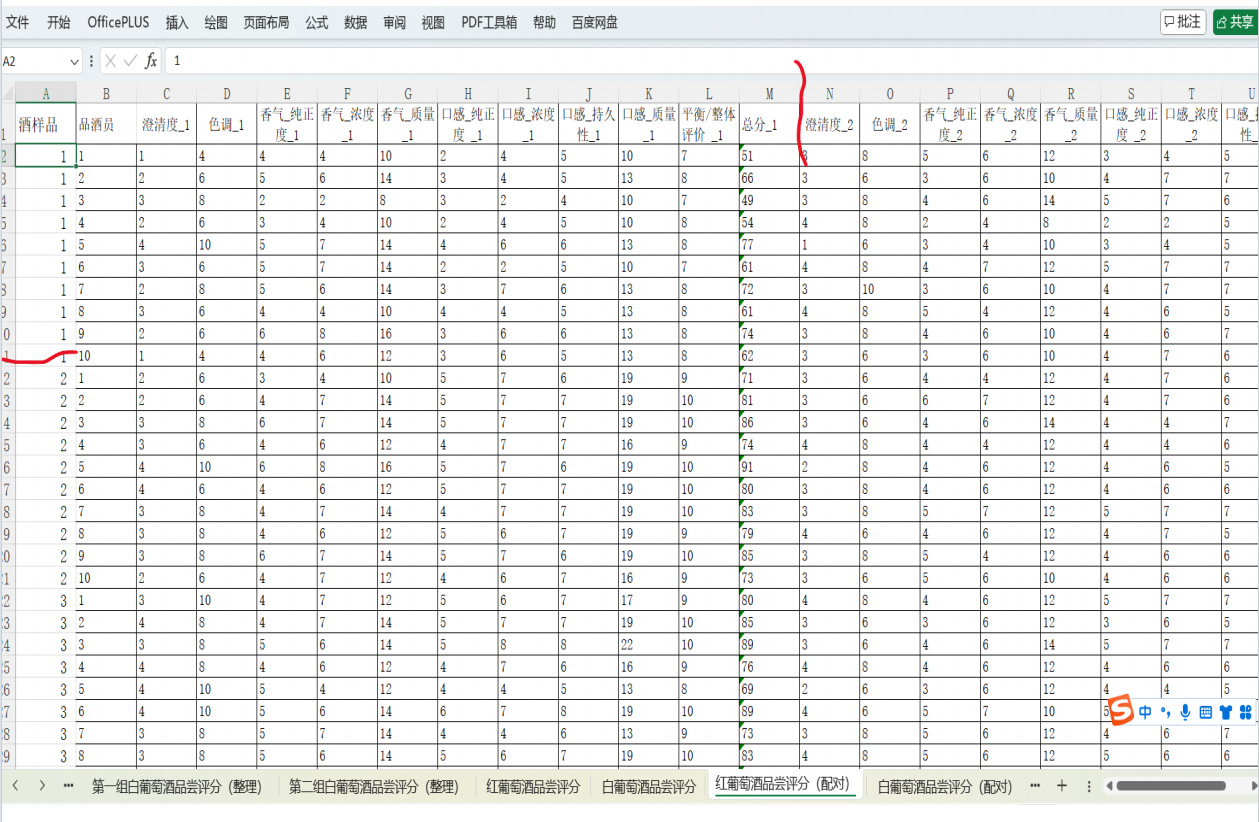
假设附件1中数据已整理为如下形式（示例）：

组1（第一组评酒员）的评分样本：

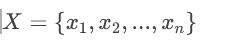
组2（第二组评酒员）的评分样本：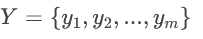

具体操作：

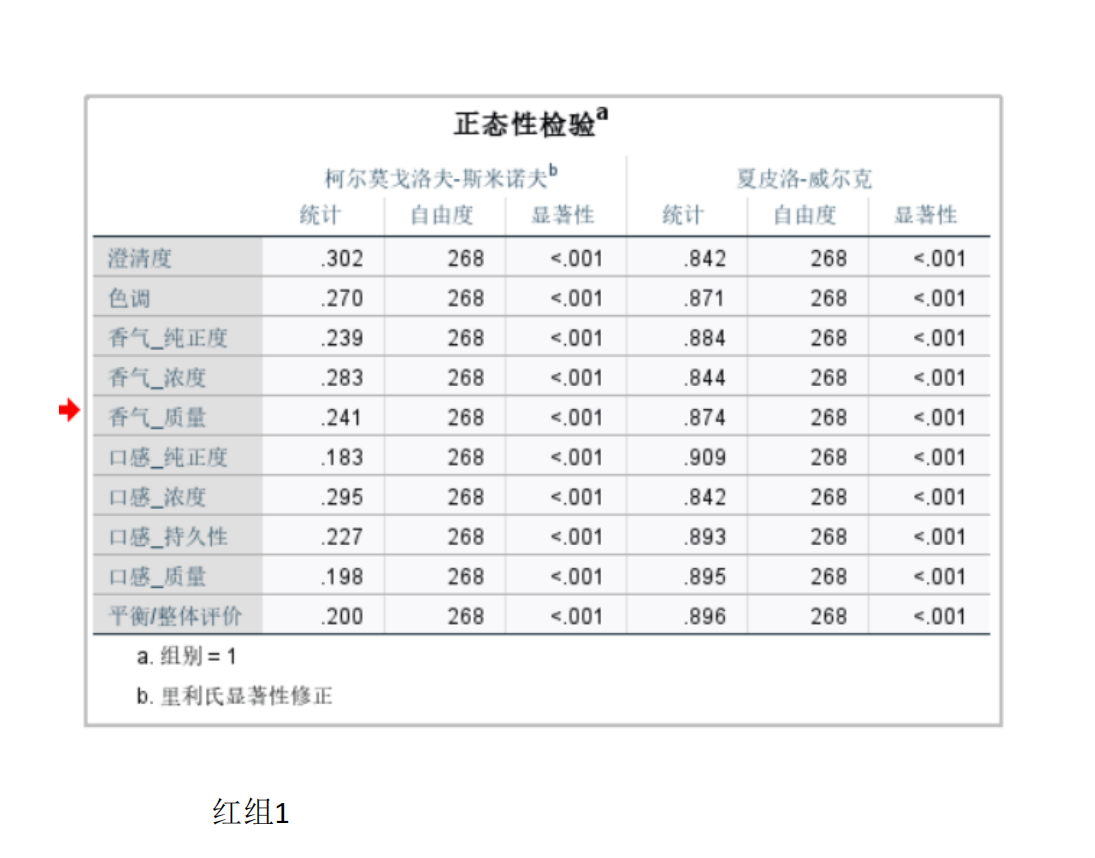
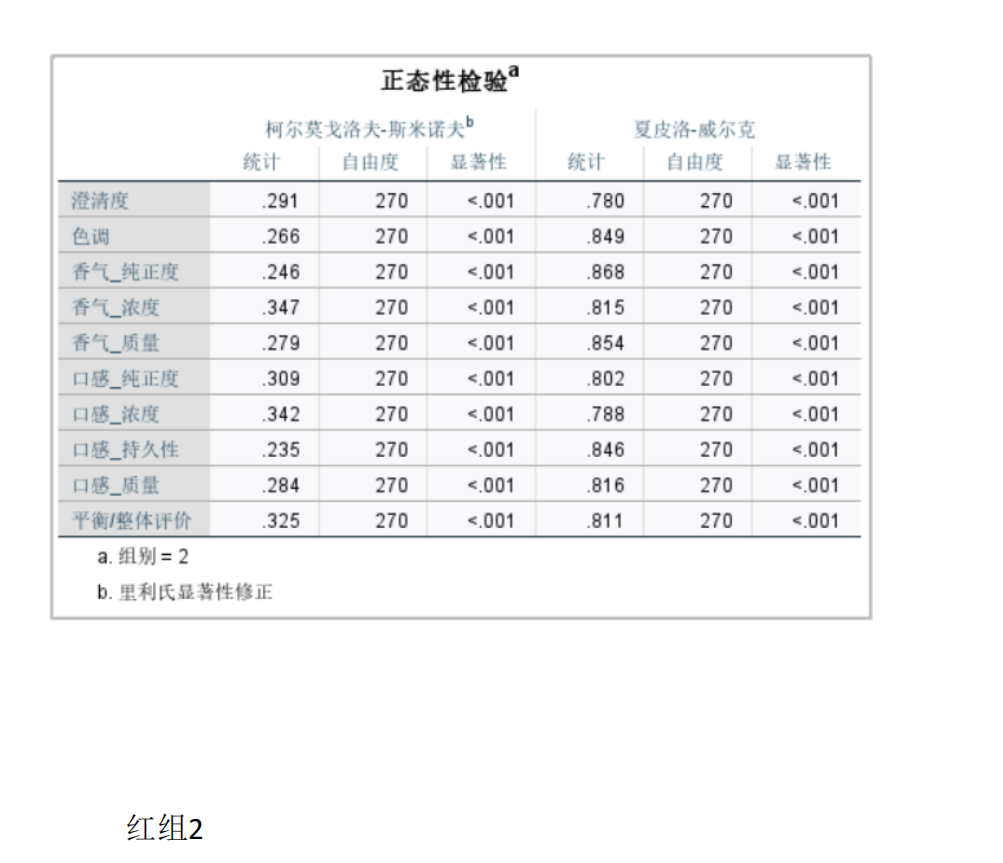
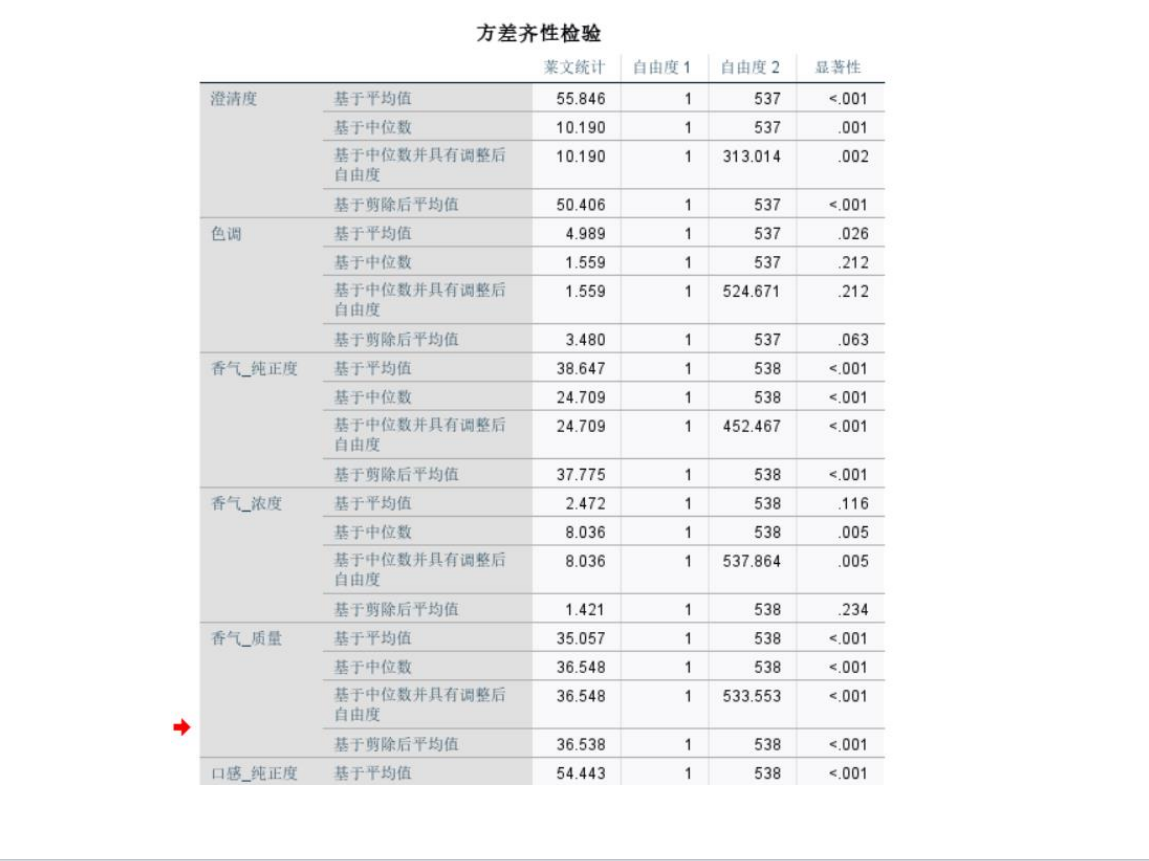
检查数据正态性（如Shapiro-Wilk检验）和方差齐性（如Levene检验）。
- 若满足正态性和方差齐性，使用两独立样本t检验：
  统计量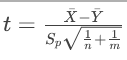，其中 Sp为合并标准差。

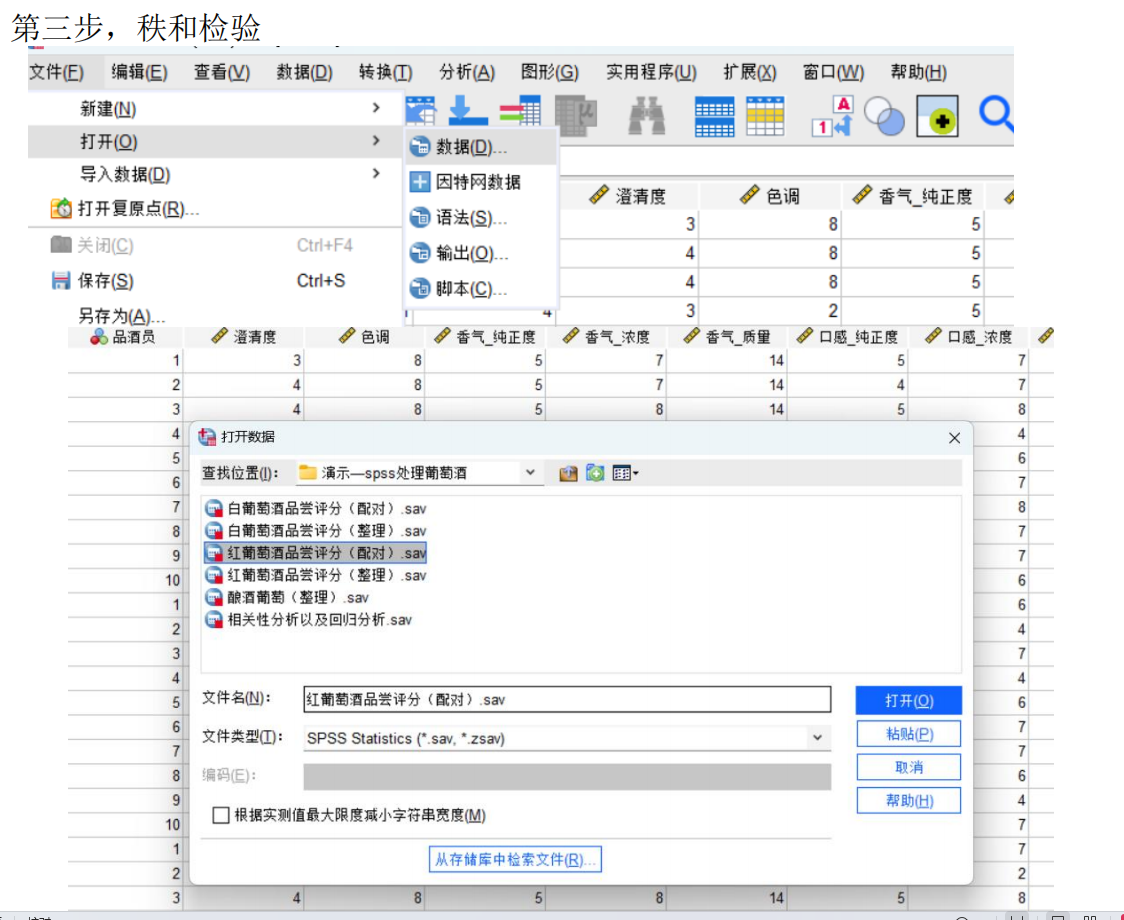
若不满足，使用Mann-Whitney U检验（秩和检验）：
统计量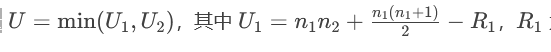为组1的秩和。

2.计算p值。

步骤5：决策规则

若p值 < α（0.05），拒绝H₀，认为两组评价存在显著差异。
若p值 ≥ α，接受H₀，认为无显著差异。

步骤6：计算并得出结论

（以实际数据计算，此处为示例流程）
假设计算得到：

t检验统计量t = -2.34，p值 = 0.021（<0.05）
→ 拒绝H₀，两组评分存在显著差异。

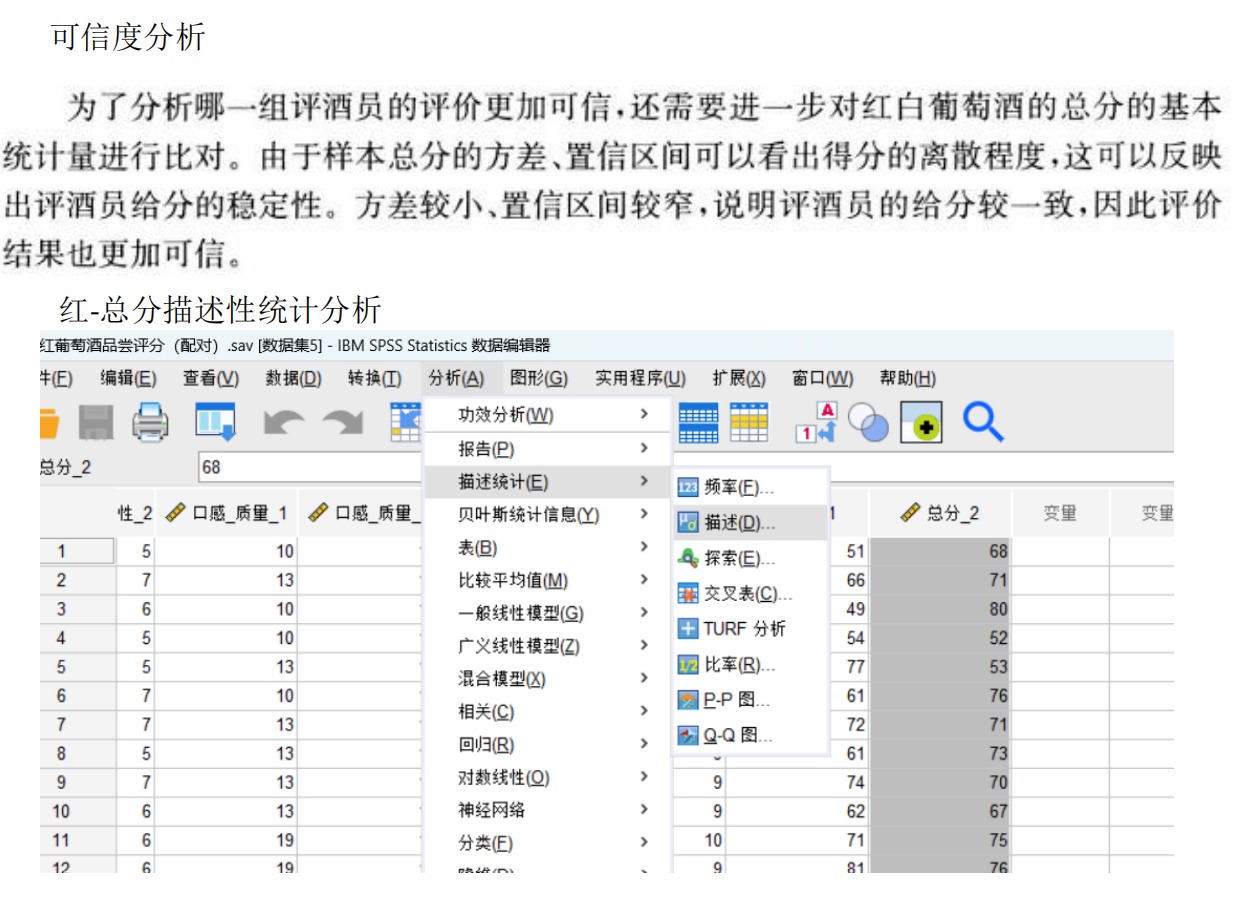
步骤7：结合可信度评价

哪一组更可信？
在存在显著差异的基础上，进一步评估可信度：

计算组内一致性（如组内评分标准差、变异系数CV或组内相关系数ICC）：
- 标准差越小、CV越小或ICC越高（接近1），说明组内评分一致性越好，可信度越高。
与客观标准关联（若存在外部基准，如葡萄酒真实质量，但本题无外部数据，故仅依赖内部一致性）。
常见结论：若一组评酒员组内一致性显著高于另一组（如更低的标准差或更高的ICC），则该组更可信。

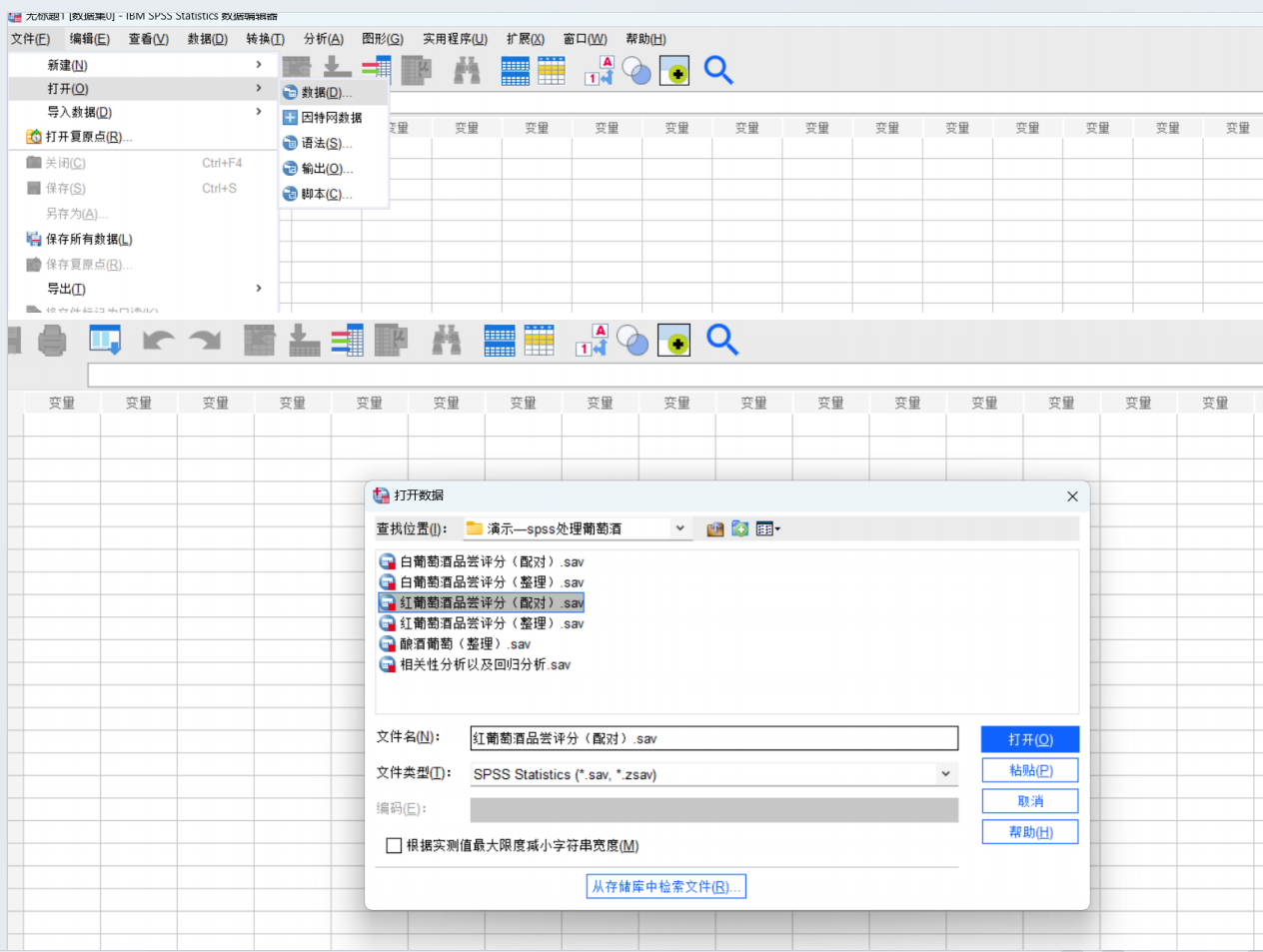
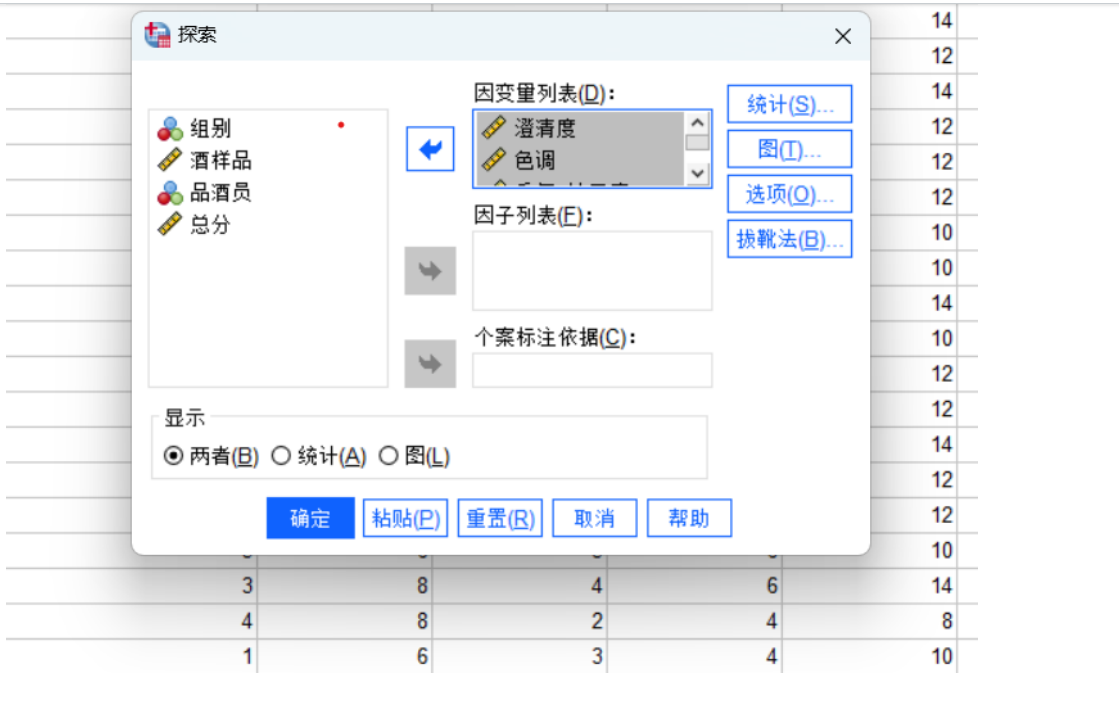
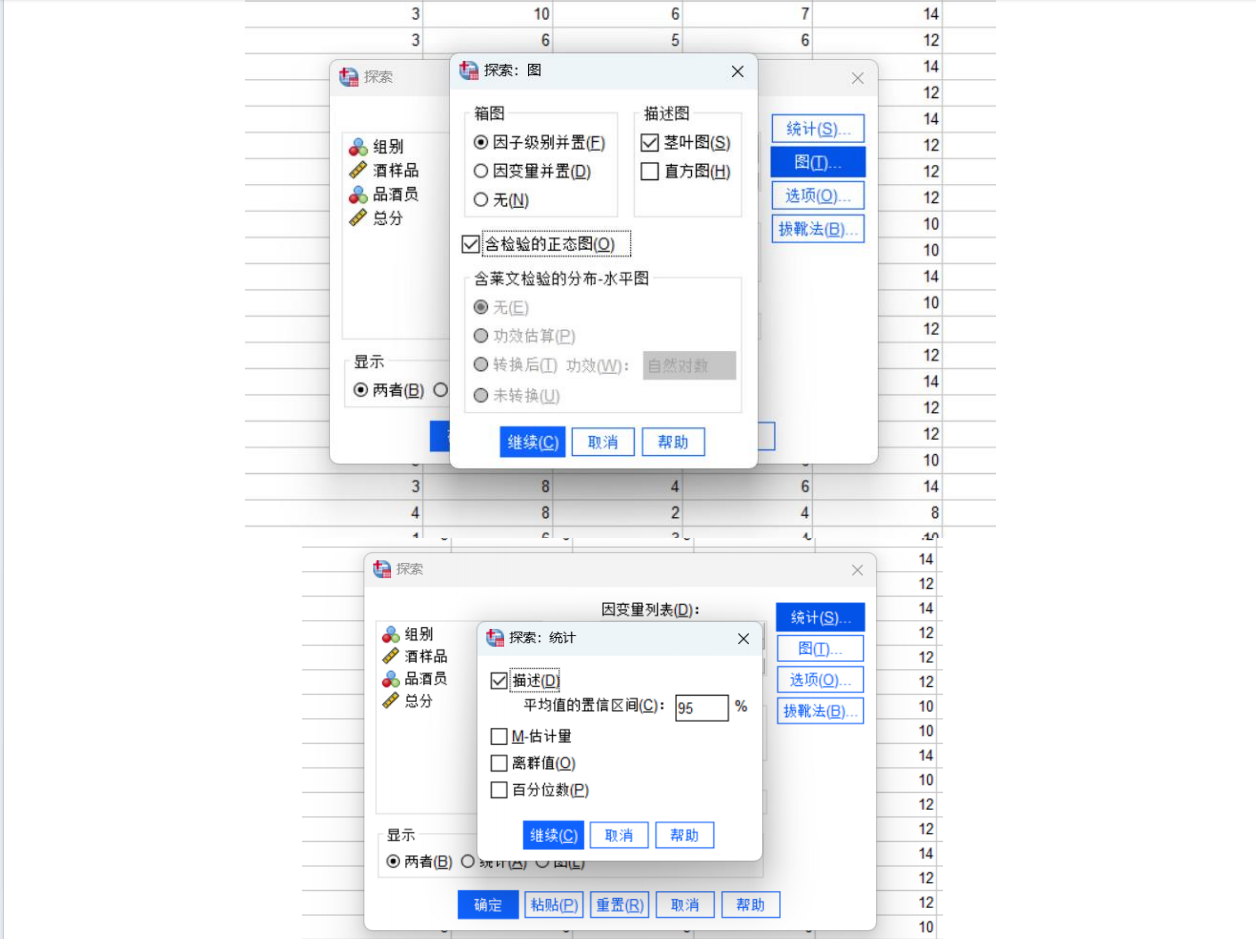
SPSS（Statistical Package for the Social Sciences，社会科学统计包）是一款非常强大且流行的统计分析软件，现在官方名称为 IBM SPSS Statistics。

一、核心概念：先理解两个主要界面

SPSS主要有两个核心窗口，几乎所有操作都在这两个窗口中进行：

数据视图：
- 长得像Excel表格。这是您直接查看、录入和修改原始数据的地方。
- 每一行代表一个案例（例如，一位受访者、一只实验小鼠、一家公司）。
- 每一列代表一个变量（例如，性别、年龄、收入、测试分数）。
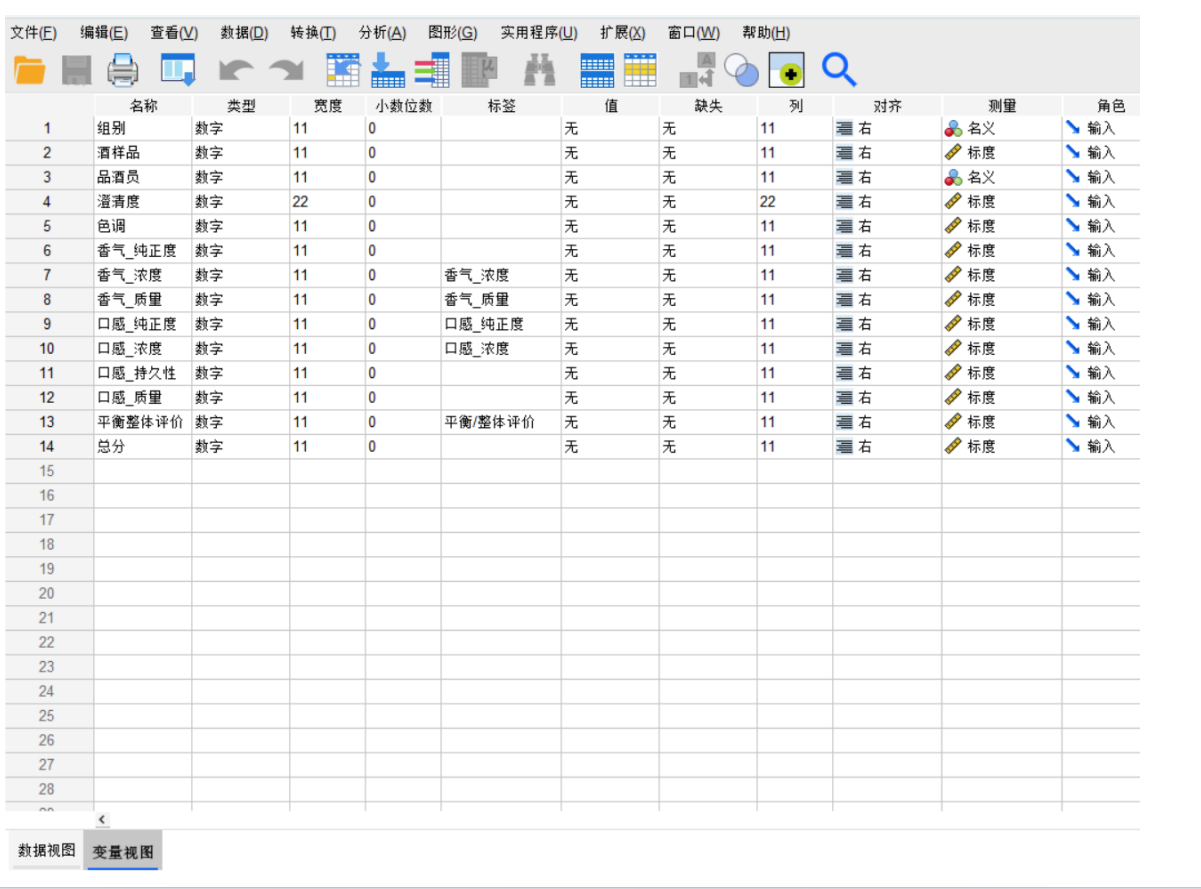
变量视图：
- 这是SPSS的灵魂所在，是定义“数据视图”中每一列（变量）属性的地方。很多新手出错都是因为没定义好变量。
- 在这里，您需要为每个变量设置关键属性：
  - 名称：变量的简短标识（如 age, gender）。
  - 类型：数字、字符串（文本）、日期等。最常用的是“数值”。
  - 宽度和小数：数字的长度和小数点位数。
  - 标签：对变量名称的详细解释（如名称是 q1，标签可以写“您对当前服务是否满意？”）。强烈建议使用，能让输出结果更易读。
  - 值：为数字代码赋值（例如，定义 1 = 男， 2 = 女）。对于分类变量至关重要！
  - 测量尺度：
    - 标度：连续数据，如年龄、收入、分数（可进行加减乘除）。
    - 有序：等级数据，如满意度（1.非常不满意，2.不满意，3.一般，4.满意，5.非常满意）。
    - 名义：分类数据，如性别、职业、省份（只是类别，无顺序和大小之分）。

简单比喻：数据视图是答卷本身，填满了答案；变量视图是答题卡上的题目说明，规定了每道题是单选还是多选，选项1代表什么，2代表什么。

二、基本操作流程

使用SPSS进行分析通常遵循以下步骤：

第1步：定义变量
在 变量视图 中，提前设置好所有需要的变量（列）及其属性（特别是“标签”和“值”）。

第2步：录入数据
切换到 数据视图，像在Excel中一样，将收集到的数据逐行（每个个案）录入进去。

第3步：数据清理和准备
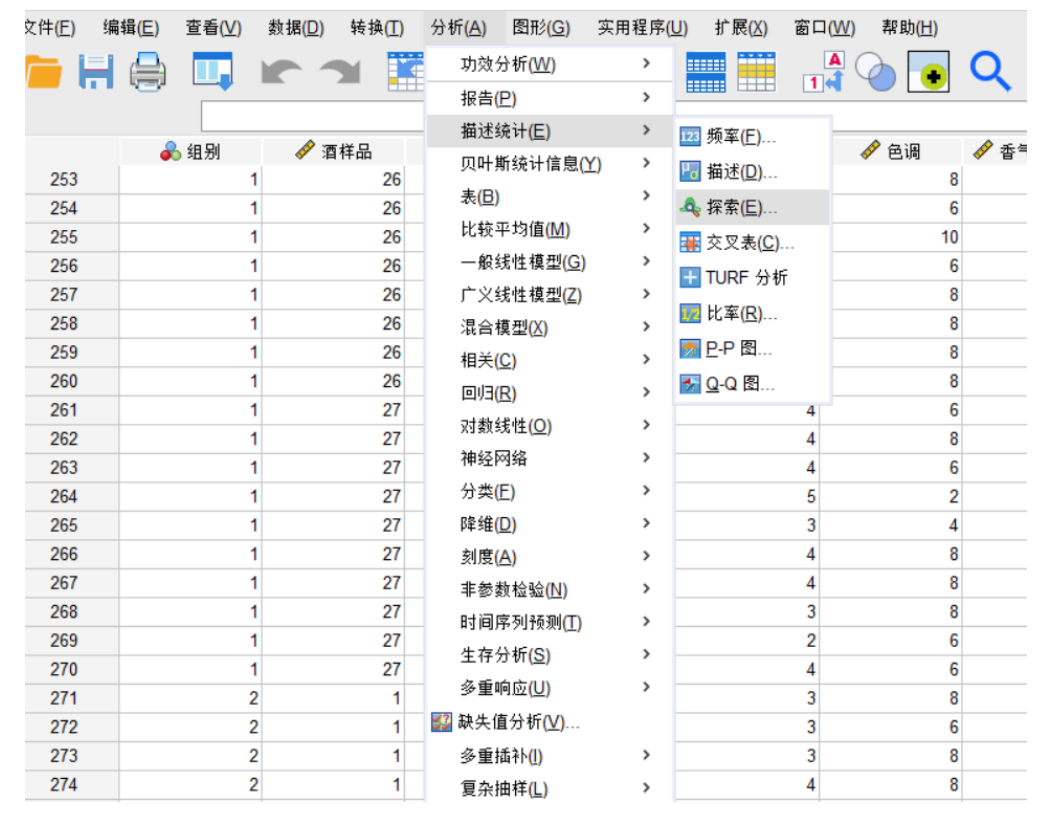
在进行分析前，通常需要检查数据。

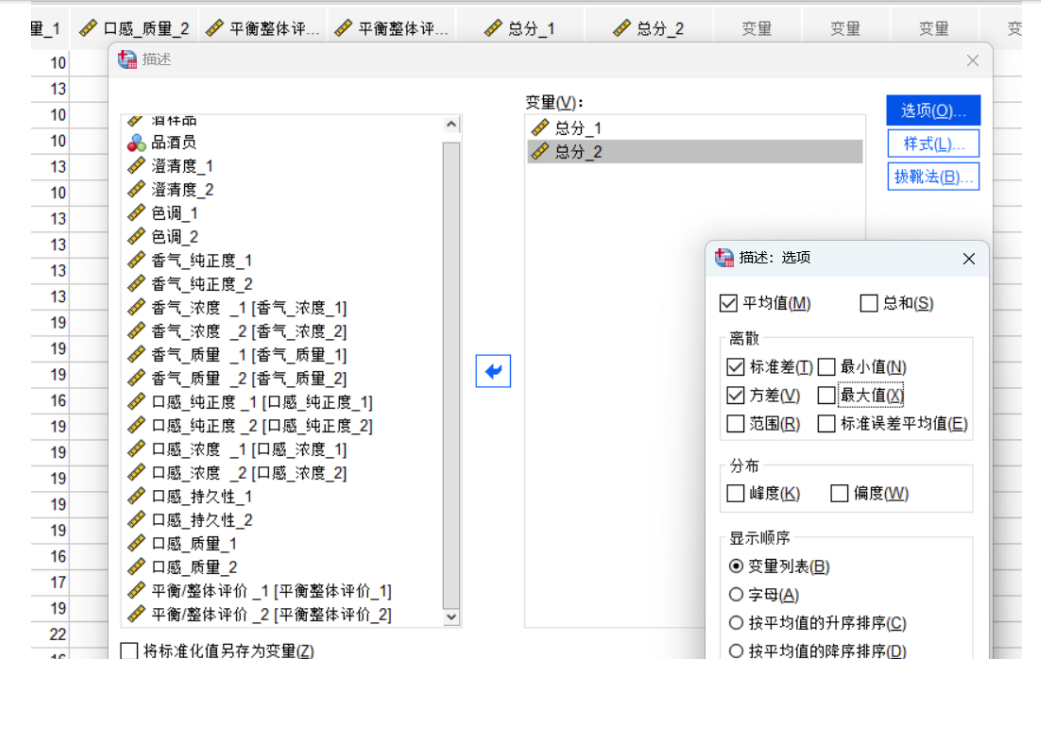
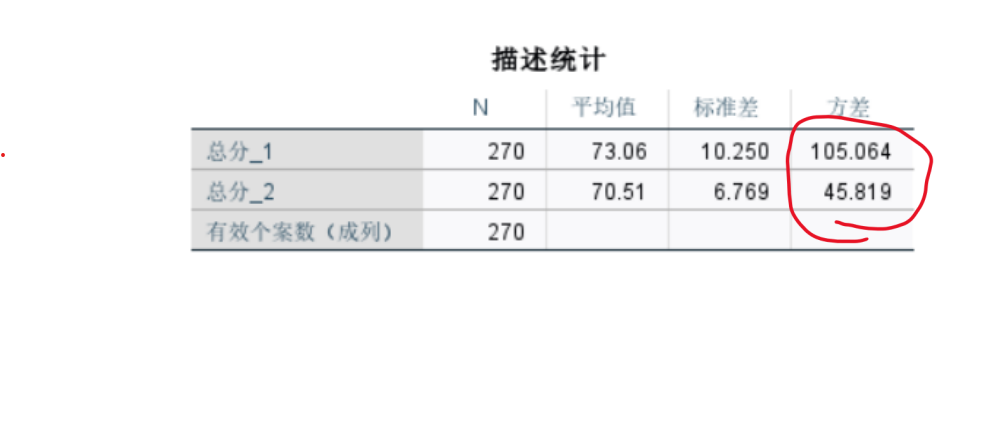
查找异常值：通过“分析” -> “描述统计” -> “频率”或“描述”来查看数据的最大最小值是否合理。
处理缺失值：检查数据中是否有空白格，并决定如何处理（删除、替换等）。
转换变量：有时需要生成新变量，例如将总收入转换为“人均收入”（转换 -> 计算变量）。

第4步：选择分析方法并执行
这是核心步骤。通过顶部的菜单栏 分析 来选择你需要的方法。

想了解基本情况？ -> 描述统计
想比较两组数据的平均值？ -> 比较均值 -> 独立样本T检验 或 配对样本T检验
想分析两个变量是否相关？ -> 相关 -> 双变量
想用多个变量预测一个结果？ -> 回归 -> 线性

第5步：解读输出结果
点击分析后，会弹出一个新的 “查看器”窗口。所有的统计表格和图表都会在这里显示。您需要根据统计学知识来解读这里的数字（如Sig./P值是否小于0.05，相关系数是多少等）。

三、常用功能快速入门

描述性统计
- 操作：分析 -> 描述统计 -> 频率 或 描述
- 用途：快速了解数据的集中趋势（平均值、中位数）和离散趋势（标准差、最小值、最大值）。频率 主要用于分类变量，能看到百分比。
T检验 - 比较两组平均值
- 独立样本T检验（比如比较男性和女性的平均收入是否不同）：
  - 分析 -> 比较均值 -> 独立样本T检验
  - 将“收入”选入检验变量，将“性别”选入分组变量，然后点击定义组，输入男和女对应的数字代码（如1和2）。
相关分析
- 操作：分析 -> 相关 -> 双变量
- 用途：分析两个或多个变量（如学习时间和考试成绩）之间的相关程度和方向。主要看“皮尔逊相关系数”和“显著性”。
回归分析
- 操作：分析 -> 回归 -> 线性
- 用途：研究一个因变量（结果）如何被多个自变量（预测因素）影响。比如“房价”如何被“面积”、“地段”、“楼层”影响。主要看R方、ANOVA表的Sig.值和系数表。
绘制图表
- 操作：图形 -> 旧对话框 -> 里面有各种图表类型（条形图、折线图、散点图等）。新版也提供了更现代的 图表构建器，可以通过拖拽方式自定义图表。

四、给新手的建议

不要害怕英文界面：SPSS有官方中文版，但很多教程和学术资源仍使用英文术语。熟悉 Variable View, Value Labels, Sig. (p-value) 等关键英文词会对你更有帮助。
从数据入手：真正理解你每个变量的含义和测量尺度，这是正确选择统计方法的基础。
边学边练：找一份简单的示范数据（网上很多），跟着教程一步一步操作，看结果是如何产生的。
理解输出：软件只会给你输出一堆数字，关键在于你能否解读出这些数字背后的统计学意义和现实意义。P值（Sig.）< 0.05 通常被认为是具有“统计学显著性”的黄金标准。
善用帮助：SPSS内置的帮助文档非常详细，遇到任何功能不懂，直接按F1或点击帮助菜单搜索。

总结一下：SPSS的操作逻辑是 “定义变量 -> 录入数据 -> 选择菜单进行分析 -> 解读输出结果”。

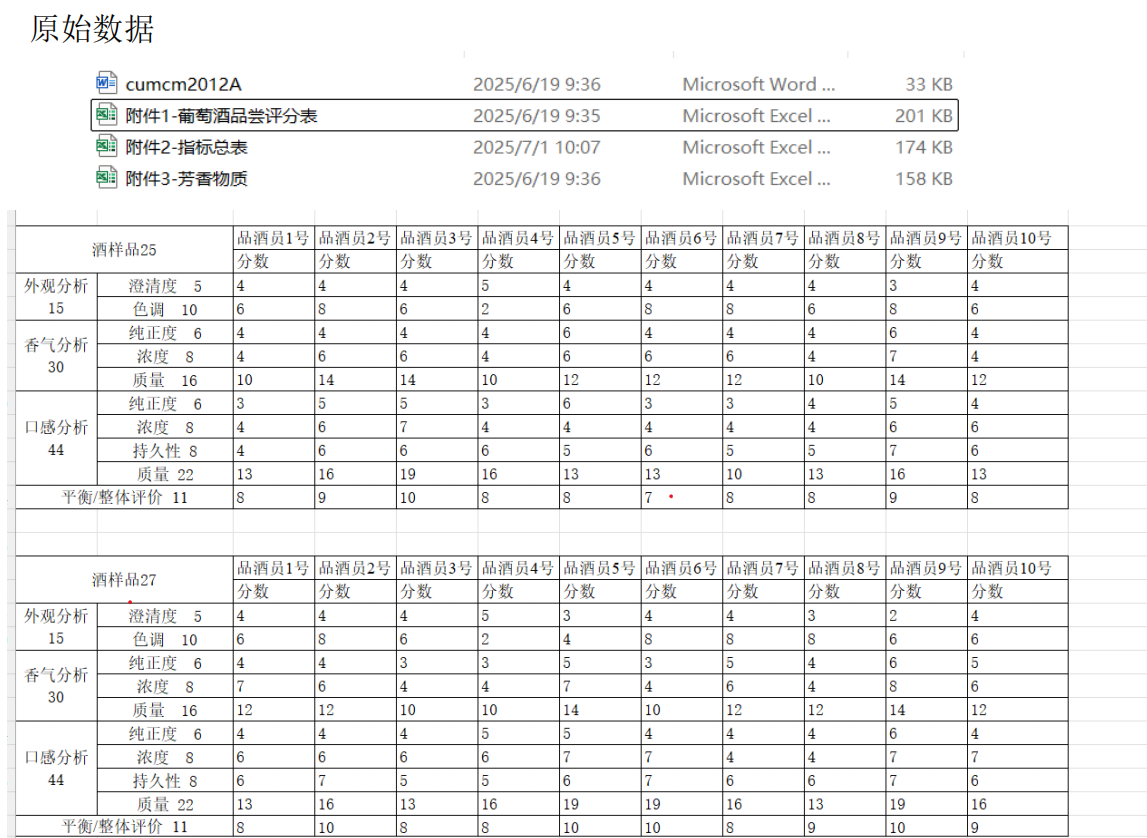
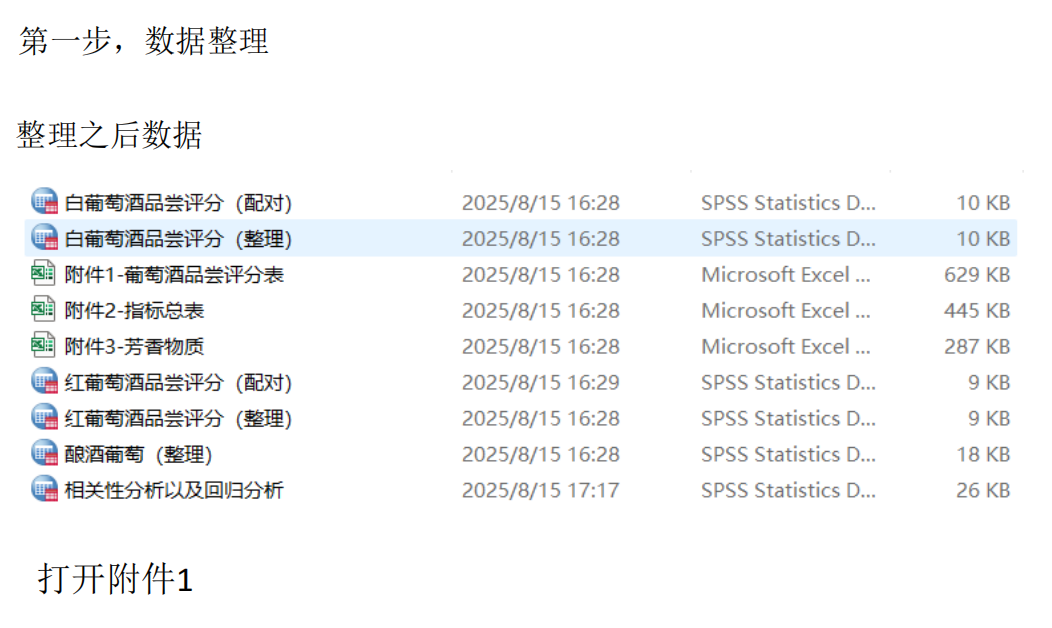
要在Python中解决葡萄酒评价问题，特别是进行假设检验和方差分析，可以使用pandas、scipy和statsmodels等库。以下是一个完整的解决方案，涵盖了如何使用Python分析不同评酒员对葡萄酒评分的差异，以及探究葡萄酒的理化指标或芳香物质对评分的影响。

一、问题重述与理解

问题背景：
分析多个葡萄酒样品的品尝评分数据，以及葡萄酒的各项理化指标和芳香物质含量数据，以确定：

不同评酒员对葡萄酒的评分是否存在显著差异。
葡萄酒的某些理化指标或芳香物质是否对评分有显著影响。

二、数据准备与预处理

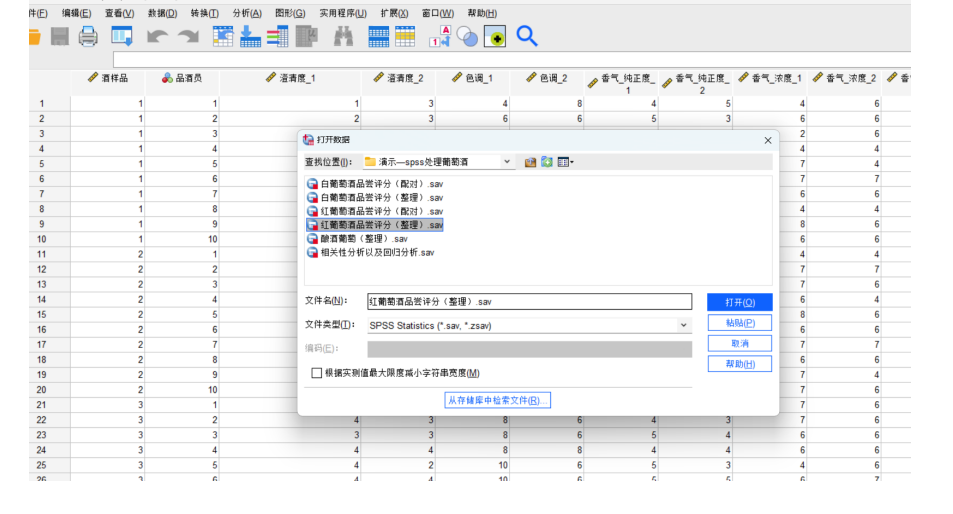
数据导入：
- 使用pandas的read_excel函数从Excel文件中导入数据。
- 假设《附件1-葡萄酒品尝评分表.xls》包含评酒员对各个葡萄酒样品的评分数据，《附件2-指标总表.xls》包含葡萄酒的各项理化指标数据，《附件3-芳香物质.xls》包含葡萄酒的芳香物质含量数据。
数据预处理：
- 检查数据完整性，处理缺失值和异常值。
- 对评分数据进行标准化处理（如果需要）。

三、假设检验与方差分析

1. 不同评酒员评分差异分析

假设：

H0（原假设）：不同评酒员对葡萄酒的评分没有显著差异。
H1（备择假设）：不同评酒员对葡萄酒的评分有显著差异。

方法：

使用单因素方差分析（One-Way ANOVA）来检验不同评酒员之间的评分是否存在显著差异。

Python实现：

import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
from statsmodels.formula.api import ols# 导入评分数据
data = pd.read_excel('附件1-葡萄酒品尝评分表.xls')# 假设数据表中有三列：'WineSample'（葡萄酒样品），'Judge'（评酒员），'Score'（评分）
# 将数据重塑为适合ANOVA的格式
grouped_data = [data[data['Judge'] == judge]['Score'].values for judge in data['Judge'].unique()]# 进行单因素方差分析
f_val, p_val = stats.f_oneway(*grouped_data)# 显示结果
print(f'ANOVA P-value: {p_val}')
if p_val < 0.05:print('拒绝原假设：不同评酒员的评分存在显著差异。')
else:print('不拒绝原假设：没有足够证据表明不同评酒员的评分存在显著差异。')# 如果需要多重比较，可以使用Tukey HSD检验（需要安装statsmodels和scikit-posthocs）
# from scikit_posthocs import posthoc_tukey
# import numpy as np
# data_for_tukey = data[['Judge', 'Score']]
# judges_unique = data['Judge'].unique()
# data_for_tukey['Judge'] = pd.Categorical(data_for_tukey['Judge'], categories=judges_unique, ordered=True)
# data_for_tukey = data_for_tukey.sort_values('Judge')
# groups = data_for_tukey.groupby('Judge')['Score'].apply(list).values
# groups = [np.array(group) for group in groups]
# post_hoc_results = posthoc_tukey(data_for_tukey, val_col='Score', group_col='Judge')
# print(post_hoc_results)

2. 理化指标和芳香物质对评分的影响分析

单因子方差分析：

对每个理化指标或芳香物质，分别进行单因子方差分析，检验其对评分的影响是否显著。

多元线性回归：
2. 如果多个理化指标或芳香物质同时影响评分，可以使用多元线性回归来探究它们对评分的联合影响。

Python实现：

单因子方差分析示例（以某一理化指标为例）：

# 导入理化指标和评分数据
indicators = pd.read_excel('附件2-指标总表.xls')# 假设我们分析的理化指标为 'Indicator1'
# 合并评分数据和理化指标数据（这里需要假设数据合并的方式，例如按葡萄酒样品ID）
# 假设 data 和 indicators 都有一个共同的列 'WineSample'
merged_data = pd.merge(data, indicators, on='WineSample')# 进行单因素方差分析（这里简单示例，实际需要按Indicator1的分组）
# 假设我们将Indicator1分成两组（高水平和低水平）进行示例
median_val = merged_data['Indicator1'].median()
high_level = merged_data[merged_data['Indicator1'] > median_val]['Score']
low_level = merged_data[merged_data['Indicator1'] <= median_val]['Score']f_val, p_val = stats.f_oneway(high_level, low_level)# 显示结果
print(f'Indicator1 ANOVA P-value: {p_val}')
if p_val < 0.05:print('Indicator1 对评分有显著影响。')
else:print('Indicator1 对评分没有显著影响。')

多元线性回归示例：

# 假设我们分析多个理化指标对评分的影响
X = merged_data[['Indicator1', 'Indicator2', 'Indicator3']]  # 示例指标
y = merged_data['Score']# 添加常数项
X = sm.add_constant(X)# 拟合多元线性回归模型
model = sm.OLS(y, X).fit()# 显示回归结果
print(model.summary())# 检查哪些指标显著
significant_indicators = model.pvalues[1:] < 0.05  # 排除截距项
print('显著的理化指标：')
print(X.columns[1:][significant_indicators])

四、结果解释与报告

对于第一问：

如果ANOVA结果显示P值小于0.05，则拒绝原假设，认为不同评酒员的评分存在显著差异。
通过多重比较（如Tukey HSD）进一步分析哪些评酒员之间的评分存在显著差异。

对于第二问：

通过单因子ANOVA和多元线性回归，可以确定哪些理化指标或芳香物质对评分有显著影响。
根据回归模型的系数和P值，可以判断各指标对评分的贡献程度和显著性。

五、具体Python操作示例（以第一问为例）

数据准备：
- 确保数据已正确导入Python，且数据已按评酒员和葡萄酒样品整理。
单因子ANOVA：
- 使用scipy.stats.f_oneway函数进行单因子方差分析。
- 记录每个因素的F值和P值，判断其是否对评分有显著影响。
多元线性回归：
- 使用statsmodels.api.OLS进行多元线性回归分析。
- 显示回归模型的系数和P值，确定哪些理化指标或芳香物质对评分有显著影响。

六、结论与报告

根据分析结果，写报告或论文，包括：

摘要：简要概述研究目的、方法和主要发现。
引言：介绍葡萄酒评价的背景和重要性。
方法：描述使用的统计方法和Python实现过程。
结果：展示ANOVA和回归分析的结果，包括显著差异和影响因素。
讨论：解释结果的实际意义，提出可能的改进或未来研究方向。

MATLAB 实现：

% 导入评分数据
data = readtable('附件1-葡萄酒品尝评分表.xls');% 假设数据表中有三列：'WineSample'（葡萄酒样品），'Judge'（评酒员），'Score'（评分）
% 将数据重塑为适合 ANOVA 的格式
judges = unique(data.Judge);
scores = {};
for i = 1:length(judges)scores{i} = data.Score(data.Judge == judges(i));
end% 进行单因素方差分析
[p, tbl, stats] = anova1(scores, judges, 'off');% 显示结果
fprintf('ANOVA P-value: %f\n', p);
if p < 0.05fprintf('拒绝原假设：不同评酒员的评分存在显著差异。\n');
elsefprintf('不拒绝原假设：没有足够证据表明不同评酒员的评分存在显著差异。\n');
end

MATLAB 实现：

单因子方差分析示例（以某一理化指标为例）：

% 导入理化指标和评分数据
indicators = readtable('附件2-指标总表.xls');
scores = data.Score; % 假设已经从评分表中获取了评分数据% 假设我们分析的理化指标为 'Indicator1'
indicatorData = indicators.Indicator1;% 进行单因素方差分析
[p, tbl, stats] = anova1([scores(indicatorData == lowLevel), scores(indicatorData == highLevel)], ...{'Low Level', 'High Level'}, 'off');% 显示结果
fprintf('Indicator1 ANOVA P-value: %f\n', p);
if p < 0.05fprintf('Indicator1 对评分有显著影响。\n');
elsefprintf('Indicator1 对评分没有显著影响。\n');
end

多元线性回归示例：

% 假设我们分析多个理化指标对评分的影响
X = [indicators.Indicator1, indicators.Indicator2, indicators.Indicator3]; % 示例指标
y = scores;% 拟合多元线性回归模型
mdl = fitlm(X, y);% 显示回归结果
disp(mdl);% 检查哪些指标显著
coefficients = mdl.Coefficients;
significantIndicators = coefficients.pValue(2:end) < 0.05; % 排除截距项
fprintf('显著的理化指标：\n');
disp(indicators.Properties.VariableNames(2:end)(significantIndicators)); % 假设前两列是指标名称，根据实际情况调整