PPO 中重要性采样

• https://github.com/modelscope/ms-swift/blob/main/docs/source/Instruction/GRPO/GetStarted/GRPO.md
• 乐，这个网页中是的groundtruth是错误的（可能是为了防止抄袭）。
  

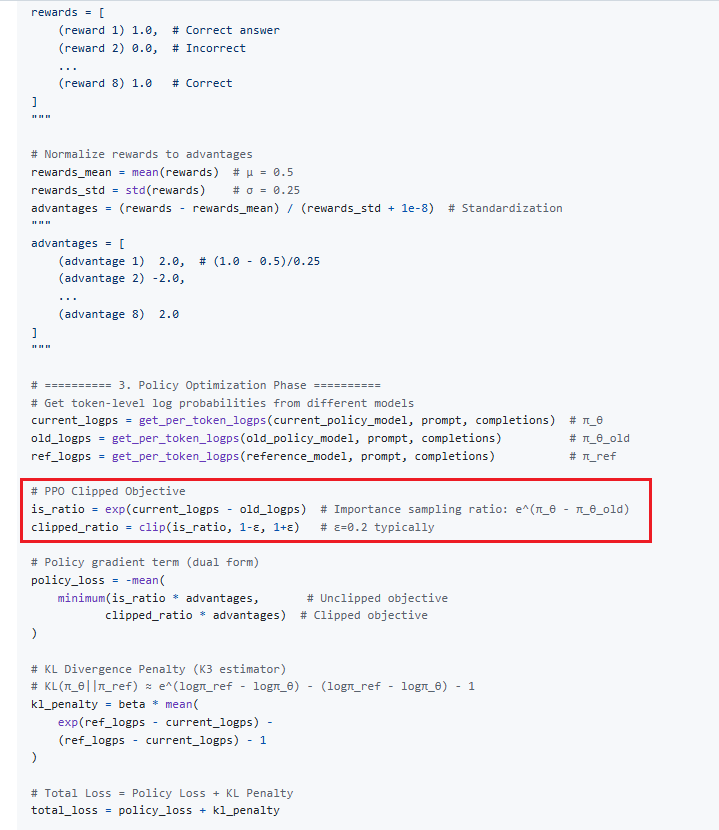
一些例子

0. 池塘养鱼的一个例子

想象一下，你想知道一个湖里所有鱼的平均重量（求期望）。

普通（均匀）采样：你租一条小船，随机在湖面上撒网。问题是，湖中心鱼又多又大，但你随机撒网，很可能大部分网都撒在了没什么鱼的岸边。这样你得撒非常多次网（采样非常多），才能得到一个比较准确的平均值。效率低下。

重要性采样：你是个聪明的渔夫。你知道湖中心的鱼又多又大（重要区域）。所以你决定：别随机撒网了，咱们就开着船专门去湖中心撒网！

新问题：这样从湖中心捞上来的鱼肯定比实际湖里的平均鱼要重，直接算平均值会严重高估。

解决方案：加权（重要性权重）。当你从湖中心捞起一条大鱼时，你在心里想：“这条鱼确实重，但它来自一个我刻意选择的‘高产区域’，所以它的代表性没那么强。我得给它打个折。”

反之，如果你偶尔在岸边捞到一条小鱼，你会想：“这条鱼虽然小，但它来自一个我几乎不采样的‘低产区域’，它能被捞上来非常难得，它的价值应该被放大。”

这个“打折”或“放大”的系数，就是 重要性权重 。通过这个权重，就能纠正你“刻意去湖中心采样”所带来的偏差，最终也能算出整个湖里鱼的真实平均重量。

核心思想：重要性采样允许我们故意从一个我们喜欢的、容易采样的分布（去湖中心） 而不是从那个原始的、难以采样的分布（整个湖面）进行抽样。然后通过一个权重来修正两个分布之间的差异，从而得到无偏的估计。

1. 强化学习

这是重要性采样最经典的应用领域之一。

问题：一个机器人要用“旧策略” π_old 收集来的数据，来学习和评估一个“新策略” π_new 的好坏。如果新策略和旧策略差别很大，那么旧数据对于新策略来说就可能很不相关，直接用它训练效果会很差甚至危险（比如新策略是“高速行驶”，而旧数据全是“低速行驶”的）。

重要性采样的应用：我们仍然使用旧策略的数据，但在用这些数据计算新策略的收益时，给每一条数据都加上一个重要性权重：权重 = (新策略采取旧行动的概率) / (旧策略采取旧行动的概率)。

例子：旧策略 π_old 在红灯时有 80% 的概率刹车，20% 的概率闯过去。新策略 π_new 更保守，在红灯时有 99% 的概率刹车，1% 的概率闯过去。

如果一条旧数据是“红灯->闯过去->发生车祸”，那么这条数据对于新策略的权重就是 (1%) / (20%) = 0.05。

这意味着，虽然“闯红灯导致车祸”这件事本身代价很大，但因为新策略几乎不会这么做（概率只有1%），所以这件事对新策略的影响会被大大折扣（权重0.05）。

反之，对于“红灯->刹车->安全”的数据，权重是 (99%) / (80%) ≈ 1.24，其影响会被适当放大。

这样，就能安全且高效地利用旧数据来优化新策略了。你提供的命令中的 --importance_sampling_level sequence 就是这个思想在 GRPO 算法中的应用。

2. 金融风险评估

问题：计算某种极端金融事件（如股市暴跌50%）发生的风险。这种事件概率极低，但后果极其严重。如果用普通的蒙特卡洛模拟，你可能要模拟成千上万次甚至百万次，才可能碰到一两次这种极端情况，效率极低。

重要性采样的应用：我们故意修改模拟的规则（采样分布），让极端事件更容易发生。比如，在模拟时故意让股价的波动性变大。

然后，在计算风险时，为每一次模拟结果加上一个权重。这个权重就是：在真实模型下，这个结果发生的概率 / 在修改后的模型下，这个结果发生的概率。

对于那些被我们“人为放大”的暴跌事件，我们会给它一个很小的权重，因为虽然它在我们的模拟中经常发生，但在现实中其实很难发生。通过权重修正后，我们就能得到它在真实世界中的正确风险值。这样，我们用几千次模拟就可能达到普通蒙特卡洛需要几百万次模拟的精度。

3. 计算机图形学（渲染）

问题：计算一个物体表面某一点的颜色（即它接收到的来自所有方向的光照积分）。来自光源方向的光线贡献很大，而来自其他方向的光线贡献很小。

重要性采样的应用：与其均匀地向所有方向发射光线去探测，不如集中地向光源的方向发射更多光线（因为那里贡献大）。

然后，在计算颜色时，为那些射向光源的光线赋予较低的权重（因为你发射了太多条了），为那些射向黑暗角落的光线赋予较高的权重（因为你发射的很少）。这样就可以用更少的光线（更快的渲染速度）得到更清晰、噪声更少的图像。