一、CT到底测了什么?
硬件动作
X 射线源与探测器阵列对置,围着物体旋转。
每转到一个角度 θ(也叫一个视角 / view),源发射扇形/平行的射线束,探测器阵列上有很多“通道/像素/bin”(记作索引 n)。
每个探测器通道在该角度接收一条射线穿过物体后的强度
。
衰减物理(Beer–Lambert)
沿射线路径,物体的线性衰减系数为
。理想单色下:
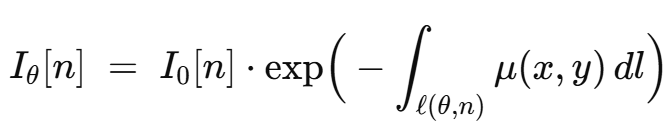
这一个标量 就是一条射线对物体的线积分(也称射线和 / ray sum)。
结论:一个角度的一个探测器通道 = 一条射线 = 一个测量值 pθ[n]。
![]()
CT 单色理想模型里,探测器在角度 θ、通道位置 s 测到的对数强度,正是把待求的衰减系数 μ(x,y)在直线 L(θ,s) 上的积分。也就是说:
![]()
正弦图 = Radon 变换的离散采样。
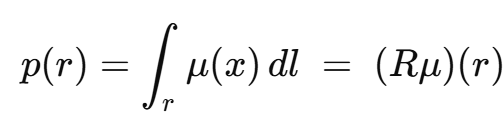
这里的 RRR(Radon 变换)是线性算子:对任意常数 a,b:
![]()
“CT 是线性的”指的就是:测量 ppp 与未知图像 μ 的关系是线性的线积分关系,因此可用 FBP 这类线性逆重建。
二、把所有测量排成“正弦图(sinogram)”
固定角度 θ,把该角度下所有通道 n=1…Ns 的
放成一行,叫一条投影。
旋转到下一个角度
,得到下一行。
堆叠所有角度 k=1…Nθ,得到一个二维数组:
![]()
这个二维数组就是正弦图。
直觉:图像中的一个点 (x0,y0)在正弦图里会沿角度画出一条正弦曲线,因此得名“sinogram”。
小例子:如果你有 600 个视角 × 641 个探测器通道,那正弦图就是一个 600×641的二维矩阵。
三、从正弦图回到图像:Radon 变换与 FBP
数学上,μ(x,y) 经Radon 变换 R 变成 p(θ,s)(连续版,s 是探测器横向坐标)。
我们手里有的就是它的离散采样 P[k,n]。
重建就是求“逆 Radon 变换”。最经典的解析法是 FBP(Filtered BackProjection,滤波反投影):
滤波:对每个角度的投影在探测器方向做 1D 滤波(斜坡滤波 + 窗函数),补偿模糊;
反投影:把每个角度、每个通道的滤波后数值,按几何关系“抹回去”加到图像像素上,所有角度累加,得到
。
Radon 变换把“图像”映成“所有直线上的积分”;在 CT 里这就是“每条射线的对数测量”。拿到它(正弦图)后,用 FBP 等逆方法就能把线积分“还原”为衰减系数图像。
FBP = “按 Radon 反演公式实现”的工程算法:先滤波补偿频谱,再反投影还原图像。
四、流程一图流(2D 切片情形)
角度 θ1: Iθ1[n] → -ln(Iθ1[n]/I0[n]) → pθ1[n] → 作为正弦图第1行
角度 θ2: Iθ2[n] → -ln(Iθ2[n]/I0[n]) → pθ2[n] → 作为正弦图第2行...
角度 θK: IθK[n] → -ln(IθK[n]/I0[n]) → pθK[n] → 作为正弦图第K行↓P[k,n](sinogram)↓FBP(每行先滤波,再把所有角度反投影求和)↓μ̂(x,y)(重建图像)
CT 就是:机器在很多角度上,用很多条射线穿过物体,探测器测到每条射线的强度 I;用同通道的空气强度 I0 归一化后做 −ln(I/I0),得到每条射线对衰减图的线积分;把所有角度与通道排成正弦图,再用 FBP/迭代法做逆 Radon 变换,重建出 μ(x,y)也就是断层重建的图像。






)












✅)