1-4、 深度学习入门-卷积神经网络(CNN)(上)-CSDN博客
5、 卷积神经网络(CNN)的实现
简单网络的构成是“Convolution - ReLU - Pooling - Affine - ReLU - Affine - Softmax”:
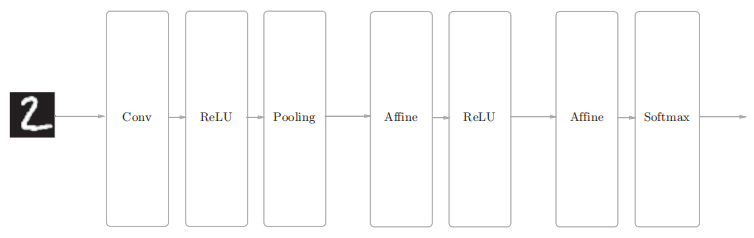
相关代码:
# 搭建进行手写数字识别的简单CNN网络
import sys, os
sys.path.append(os.pardir)
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradientclass SimpleConvNet:"""简单的ConvNetconv - relu - pool - affine - relu - affine - softmaxParameters----------input_size : 输入大小(MNIST的情况下为784)input_dim―输入数据的维度:(通道,高,长)conv_param―卷积层的超参数(字典)。字典的关键字如下:filter_num―滤波器的数量ilter_size―滤波器的大小stride―步幅pad―填充hidden_size―隐藏层(全连接)的神经元数量hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100])output_size : 输出大小(MNIST的情况下为10)activation : 'relu' or 'sigmoid'weight_init_std : 初始化时权重的标准差(e.g. 0.01)指定'relu'或'he'的情况下设定“He的初始值”指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”"""# 初始化的最开始部分def __init__(self, input_dim=(1, 28, 28),# 卷积层的超参数通过名为conv_param的字典传入,# 以{'filter_num':30,'filter_size':5, 'pad':0, 'stride':1}保存必要的超参数值conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},hidden_size=100, output_size=10, weight_init_std=0.01):# 将由初始化参数传入的卷积层的超参数从字典中取了出来(以方便后面使用)filter_num = conv_param['filter_num']filter_size = conv_param['filter_size']filter_pad = conv_param['pad']filter_stride = conv_param['stride']input_size = input_dim[1]# 计算卷积层的输出大小conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))# 初始化权重参数# 将这些参数保存在实例变量的params字典中self.params = {}# 将第1层的卷积层的权重设为关键字W1,偏置设为关键字b1self.params['W1'] = weight_init_std * \np.random.randn(filter_num, input_dim[0], filter_size, filter_size)self.params['b1'] = np.zeros(filter_num)# 分别用关键字W2、b2和关键字W3、b3来保存第2个和第3个全连接层的权重和偏置self.params['W2'] = weight_init_std * \np.random.randn(pool_output_size, hidden_size)self.params['b2'] = np.zeros(hidden_size)self.params['W3'] = weight_init_std * \np.random.randn(hidden_size, output_size)self.params['b3'] = np.zeros(output_size)# 生成层self.layers = OrderedDict()# 从最前面开始按顺序向有序字典(OrderedDict)的layers中添加层self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],conv_param['stride'], conv_param['pad'])self.layers['Relu1'] = Relu()self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])self.layers['Relu2'] = Relu()self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])# SoftmaxWithLoss层被添加到另一个变量lastLayer中self.last_layer = SoftmaxWithLoss()def predict(self, x):for layer in self.layers.values():x = layer.forward(x)return xdef loss(self, x, t):"""求损失函数参数x是输入数据、t是正确标签"""# 用于推理的predict方法从头开始依次调用已添加的层,并将结果传递给下一层y = self.predict(x)return self.last_layer.forward(y, t)def accuracy(self, x, t, batch_size=100):if t.ndim != 1 : t = np.argmax(t, axis=1)acc = 0.0for i in range(int(x.shape[0] / batch_size)):tx = x[i*batch_size:(i+1)*batch_size]tt = t[i*batch_size:(i+1)*batch_size]y = self.predict(tx)y = np.argmax(y, axis=1)acc += np.sum(y == tt) return acc / x.shape[0]def numerical_gradient(self, x, t):"""求梯度(数值微分)Parameters----------x : 输入数据t : 教师标签Returns-------具有各层的梯度的字典变量grads['W1']、grads['W2']、...是各层的权重grads['b1']、grads['b2']、...是各层的偏置"""loss_w = lambda w: self.loss(x, t)grads = {}for idx in (1, 2, 3):grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])return gradsdef gradient(self, x, t):"""求梯度(误差反向传播法)Parameters----------x : 输入数据t : 教师标签Returns-------具有各层的梯度的字典变量grads['W1']、grads['W2']、...是各层的权重grads['b1']、grads['b2']、...是各层的偏置"""# forwardself.loss(x, t)# backwarddout = 1dout = self.last_layer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:dout = layer.backward(dout)# 设定grads = {}grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].dbgrads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn gradsdef save_params(self, file_name="params.pkl"):params = {}for key, val in self.params.items():params[key] = valwith open(file_name, 'wb') as f:pickle.dump(params, f)def load_params(self, file_name="params.pkl"):with open(file_name, 'rb') as f:params = pickle.load(f)for key, val in params.items():self.params[key] = valfor i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):self.layers[key].W = self.params['W' + str(i+1)]self.layers[key].b = self.params['b' + str(i+1)]# 学习
import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch07.simple_convnet import SimpleConvNet
from common.trainer import Trainer# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)# 处理花费时间较长的情况下减少数据
#x_train, t_train = x_train[:5000], t_train[:5000]
#x_test, t_test = x_test[:1000], t_test[:1000]max_epochs = 20network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},hidden_size=100, output_size=10, weight_init_std=0.01)trainer = Trainer(network, x_train, t_train, x_test, t_test,epochs=max_epochs, mini_batch_size=100,optimizer='Adam', optimizer_param={'lr': 0.001},evaluate_sample_num_per_epoch=1000)
trainer.train()# 保存参数
network.save_params("params.pkl")
print("Saved Network Parameters!")# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()运行结果:
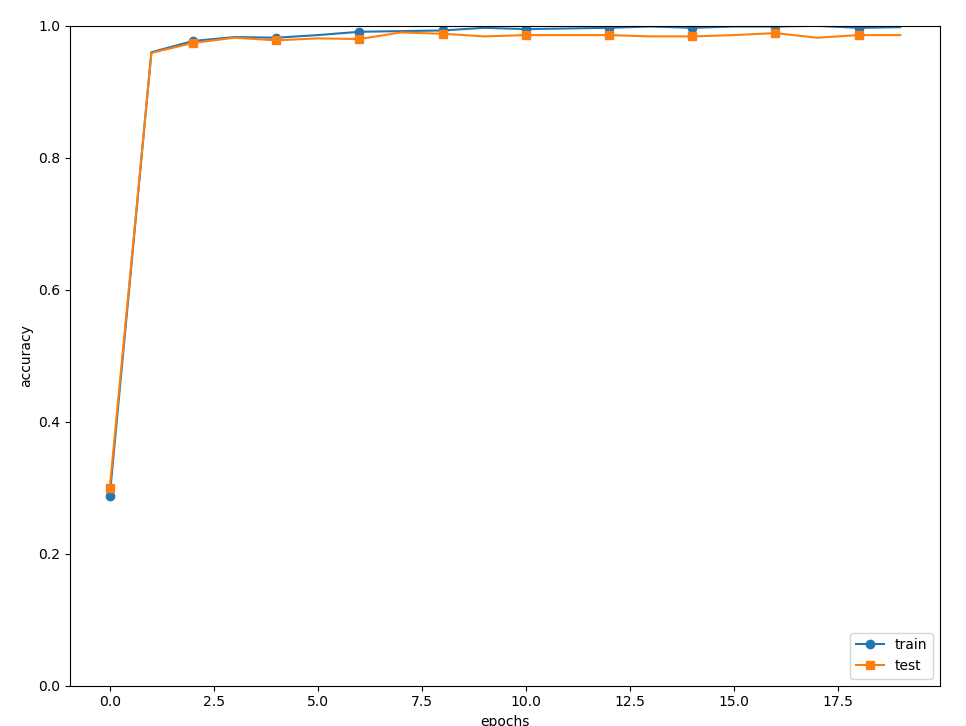
如上运行结果:
如果使用MNIST数据集训练SimpleConvNet,则训练数据的识别率为99.82%,测试数据的识别率为98.91%(会有一些误差)。测试数据的识别率大约为99%,就小型网络来说,这是一个非常高的识别率。
6、 卷积神经网络(CNN)的可视化
6.1、第1层(卷积层)权重的可视化
将卷积层(第1层)的滤波器显示为图像,然后来比较一下学习前和学习后的权重:
代码:
# 卷积层权重的可视化
import numpy as np
import matplotlib.pyplot as plt
from ch07.simple_convnet import SimpleConvNetdef filter_show(filters, nx=8, margin=3, scale=10):"""c.f. https://gist.github.com/aidiary/07d530d5e08011832b12#file-draw_weight-py"""FN, C, FH, FW = filters.shapeny = int(np.ceil(FN / nx))fig = plt.figure()fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)for i in range(FN):ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')plt.show()network = SimpleConvNet()
# 随机进行初始化后的权重
filter_show(network.params['W1'])# 学习后的权重
network.load_params("params.pkl")
filter_show(network.params['W1'])运行结果:
学习前:

学习后:

观察运行结果发现,学习后的滤波器在有规律地观察边缘(颜色变化的分界线)和斑块(局部的块状区域)等。
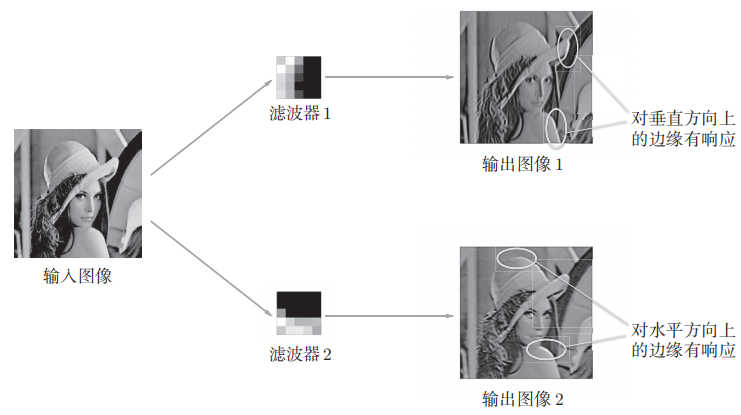
如下图显示了选择两个学习完的滤波器对输入图像进行卷积处理时的结果。我们发现“滤波器1”对垂直方向上的边缘有响应,“滤波器2”对水平方向上的边缘有响应。
6.2、基于分层结构的信息提取
上述结果是针对第1层的卷积层得出的。第1层的卷积层中提取了边缘或斑块等“低级”信息。
在堆叠了多层的CNN中,则随着层次加深,提取的信息也愈加复杂、抽象。
最开始的层对简单的边缘有响应,接下来的层对纹理有响应,再后面的层对更加复杂的物体部件有响应。也就是说,随着层次加深,神经元从简单的形状向“高级”信息变化。
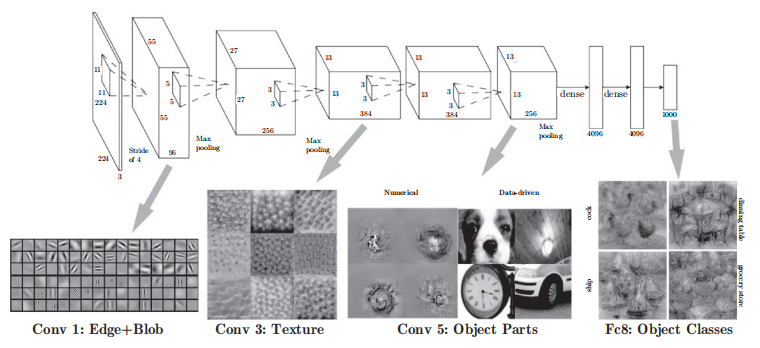
如下图,CNN的卷积层中提取的信息。第1层的神经元对边缘或斑块有响应,第3层对纹理有响应,第5层对物体部件有响应,最后的全连接层对物体的类别(狗或车)有响应。
7、 具有代表性的 CNN:LeNet、AlexNet
7.1、LeNet
LeNet是进行手写数字识别的网络。如下图,它有连续的卷积层和池化层(只“抽选元素”的子采样层),最后经全连接层输出结果。
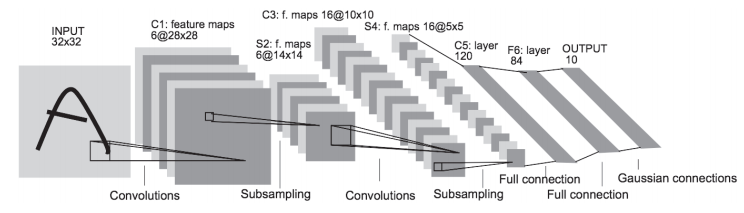
特点:
激活函数为sigmoid函数
使用子采样(subsampling)缩小中间数据的大小
7.2、AlexNet
AlexNet叠有多个卷积层和池化层,最后经由全连接层输出结果。
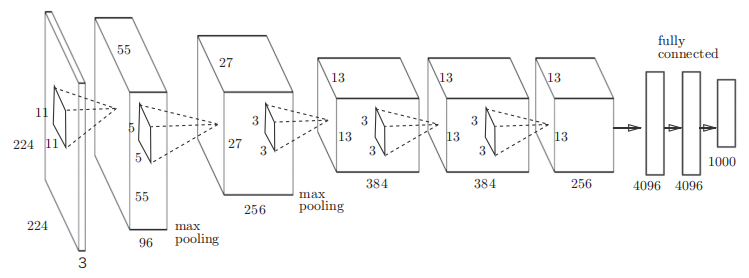
特点:
激活函数为ReLU函数
使用Max池化缩小中间数据的大小
使用进行局部正规化的LRN(Local Response Normalization)层
使用Dropout
)








)
)
)



)


![[BrowserOS] Nxtscape浏览器核心 | 浏览器状态管理 | 浏览器交互层](http://pic.xiahunao.cn/[BrowserOS] Nxtscape浏览器核心 | 浏览器状态管理 | 浏览器交互层)
