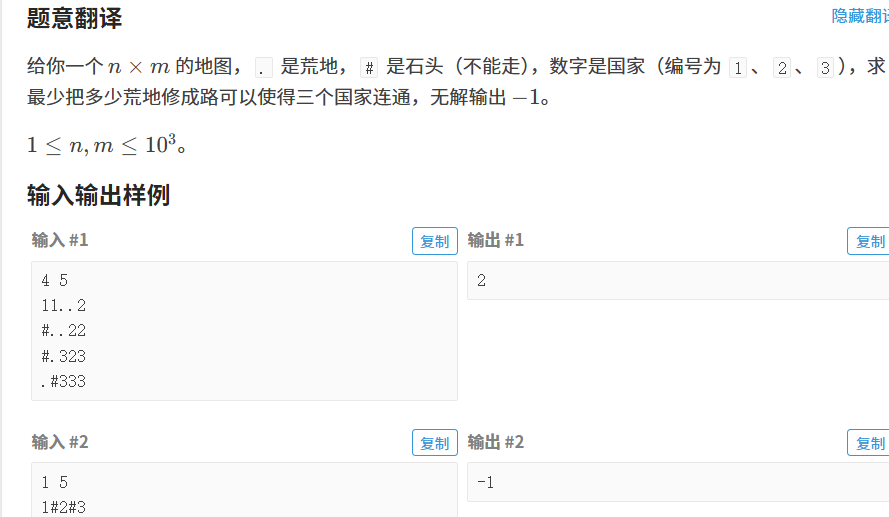
审题：

本题需要我们找到最佳铺设道路，将三个国家联通起来，然后输出最佳铺设道路的铺设数量，若没有联通方法则输出-1

思路：

首先我们正面思考：只需从某个点出发然后搜索到三个国家即可，最后对比所有距离中最小的

缺陷：这种方法需要考虑的前提很多，我们的国家不一定是连在一起的，可能都分开，可能其中两个国家连起来，有可能都是直接连起来的，所以不太好写代码

正难则反：我们可以从每个国家开始搜索，搜索出三张铺设图，然后根据这三张图的数据对每个非#点进行距离计算，最后筛出最短铺设数并输出

搜索方法：01BFS

由于铺设的时候遇到荒地可以铺设，遇到国家的时候不用铺设，所以对于铺设数的权值就是0和1.我们就可以采用01bfs了

解题：
 

#include<iostream>
#include<cstring>
#include<deque>
using namespace std;
const int N = 1010;
typedef pair<int, int> PII;
int n, m;
char a[N][N];
int dis[4][N][N];
int dx[] = { 1,-1,0,0 };
int dy[] = { 0,0,1,-1 };
void bfs(int num)
{//清除痕迹deque<PII> q;memset(dis[num], -1, sizeof dis[num]);//源点放入dequefor (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (num == a[i][j] - '0'){q.push_back({ i,j });dis[num][i][j] = 0;}}}//01bfswhile (q.size()){PII t = q.front(); q.pop_front();int x0 = t.first, y0 = t.second;for (int k = 0; k < 4; k++){int x = x0 + dx[k], y = y0 + dy[k];if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] != '#'){char next = a[x][y];int w = (next == '.' ? 1 : 0);if (dis[num][x][y] == -1)//首次遇到{dis[num][x][y] = dis[num][x0][y0] + w;if (w == 0) q.push_front({ x,y });else q.push_back({ x,y });}else if(dis[num][x0][y0] + w < dis[num][x][y])//松弛操作{dis[num][x][y] = dis[num][x0][y0] + w;}}}}
}
int main()
{//数据录入cin >> n >> m;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];}}//搜索出三张铺设图bfs(1); bfs(2); bfs(3);//根据三张图筛出结果并输出int ret = 0x3f3f3f3f;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (a[i][j] == '#') continue;//石头无法联通int x = dis[1][i][j], y = dis[2][i][j], z = dis[3][i][j];if (x == -1 || y == -1 || z == -1) continue;//该点到达不了if (a[i][j] == '.')//减去重复铺设的格子{ret = min(ret, x + y + z - 2);}else{ret = min(ret, x + y + z);}}}if (ret == 0x3f3f3f3f){cout << -1 << endl;}else{cout << ret << endl;}return 0;
}

注意：

1.最后在统计的时候遇到石头是可以直接跳过的，而当距离中存在负数的时候说明有一个国家是无法到达的，此时也可以直接跳过

2.对于统计点为荒地的时候由于该地会被铺设三次，所以我们需要减2，统计国家地块的时候我们就直接加就行了，因为国家地块是不会进行铺设的，所以不存在重复铺设的情况

CF590C Three States - 洛谷