面试高频题力扣 417. 太平洋大西洋水流问题洪水灌溉(FloodFill) 深度优先遍历(dfs) 暴力搜索 C++解题思路每日一题

零、题目描述：用人话再讲一遍
一、为什么这道题值得咱们学习？
二、思路探索
- 常规思路：逐个检查每个格子（会超时！⚠️）
三、正难则反：反向思维的巧妙应用 🔄
（思考时间！）💡
四、代码实现：一步步拆解
- 代码拆解:
- 时间复杂度分析
- 空间复杂度分析
六、坑点总结 & 举一反三 🚀

嗨，各位算法爱好者！今天咱们来讨论一道有点绕但超经典的题目—— LeetCode 417. 太平洋大西洋水流问题。这道题堪称“洪水灌溉”系列的进阶版，学好它，能让你的逆向思维能力上个大台阶！

零、题目描述：用人话再讲一遍

在这里插入图片描述

这道题力扣上面的题目表述太难评了，本来挺简单的一道题让力扣的描述说的好像一道外星题，我就不过多说明力扣的题目描述，用我自己的话来向大家解释下这道题：

题目核心：
给你一个 m x n 的网格（可以想象成一个岛屿的地形图）

每个坐标都有自己的高度值 🏔️
岛屿的上边界和左边界挨着太平洋 🌊
岛屿的下边界和右边界挨着大西洋 🌊
水往低处流或者平流（即水可以向<=自己高度值的坐标里流动）
这道题要我们返回的就是既能流到太平洋，又能流到大西洋的格子坐标。

举个栗子 🌰：
如果一个格子的水，既能一路向左/向上流到太平洋，又能一路向右/向下流到大西洋，那它就是我们要找的目标！

我们用示例1来说明：👇

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

以坐标 [2,2]（第三行第三列，高度 5 ）为例，快速模拟验证逻辑：

我们来以 [2,2]也就就是图中最中间的5这个坐标模拟流水

先是流向太平洋：
[2,2] (5) → [1,2] (3)（上，3≤5）→ [0,2] (2)（上，2≤3）→ 触达第 0 行（太平洋边界）

之后是流大西洋：
[2,2] (5) → [3,2] (1)（下，1≤5）→ [4,2] (1)（下，1≤1）→ 触达第 4 行（大西洋边界）

这些黄色格子要么本身就在海洋边界（直接满足流向对应海洋），要么能通过 “向更低 / 等高单元格流动” 的规则，连通到太平洋或大西洋的边界。通过这样的水流逻辑，它们被判定为 “既能流向太平洋，又能流向大西洋”，所以出现在最终结果里。你可以结合网格图，顺着水流方向模拟一遍，就能更直观理解啦～

一、为什么这道题值得咱们学习？

这道题简直是逆向思维的绝佳教材！它的精髓在于：

打破“从起点找终点”的固定思维，学会“正难则反”（当正面求解复杂时，试试反过来想）
进一步巩固洪水灌溉（Flood Fill） 算法的应用
训练二维网格中“区域标记”与“交集计算”的能力

💡 悄悄说：这道题和咱们专栏中的第一篇博客力扣 200.岛屿数量是递进关系哦！如果还没看过建议先去看一看那一篇博客，讲了DFS的基础实现，我们专栏中的上一篇博客力扣 130. 被围绕的区域则铺垫了“正难则反”的思路，循序渐进效果更佳～感兴趣的朋友可以订阅我的专栏每日一题，我会每天发一篇关于算法练习的博客哦，专栏中的博客也都是有着层层递进的联系的~

二、思路探索

常规思路：逐个检查每个格子（会超时！⚠️）

最直观的想法：遍历每个格子，分别判断它能否流到太平洋和大西洋。

步骤：

对每个格子 (i,j)，调用 canFlowToPacific(i,j) 和 canFlowToAtlantic(i,j)
两个函数都返回 true 时，加入结果集

实现草图：

// 检查(i,j)能否流到太平洋
bool canFlowToPacific(int i, int j, vector<vector<int>>& heights) {if (i == 0 || j == 0) return true; // 已到达太平洋边界for (四个方向) {int ni = i + dx[k], nj = j + dy[k];if ( heights[ni][nj] <= heights[i][j] ) { // 能往低处流if (canFlowToPacific(ni, nj, heights)) return true;}}return false;
}
// 大西洋同理...

为什么会超时？

每个格子可能被重复检查多次，时间复杂度高达 O((m*n)^2)
对于 300x300 的网格，运算量会达到惊人的 8100 万²，直接爆掉！

结果也是如此，我已经替大家试过了/(ㄒoㄒ)/~~
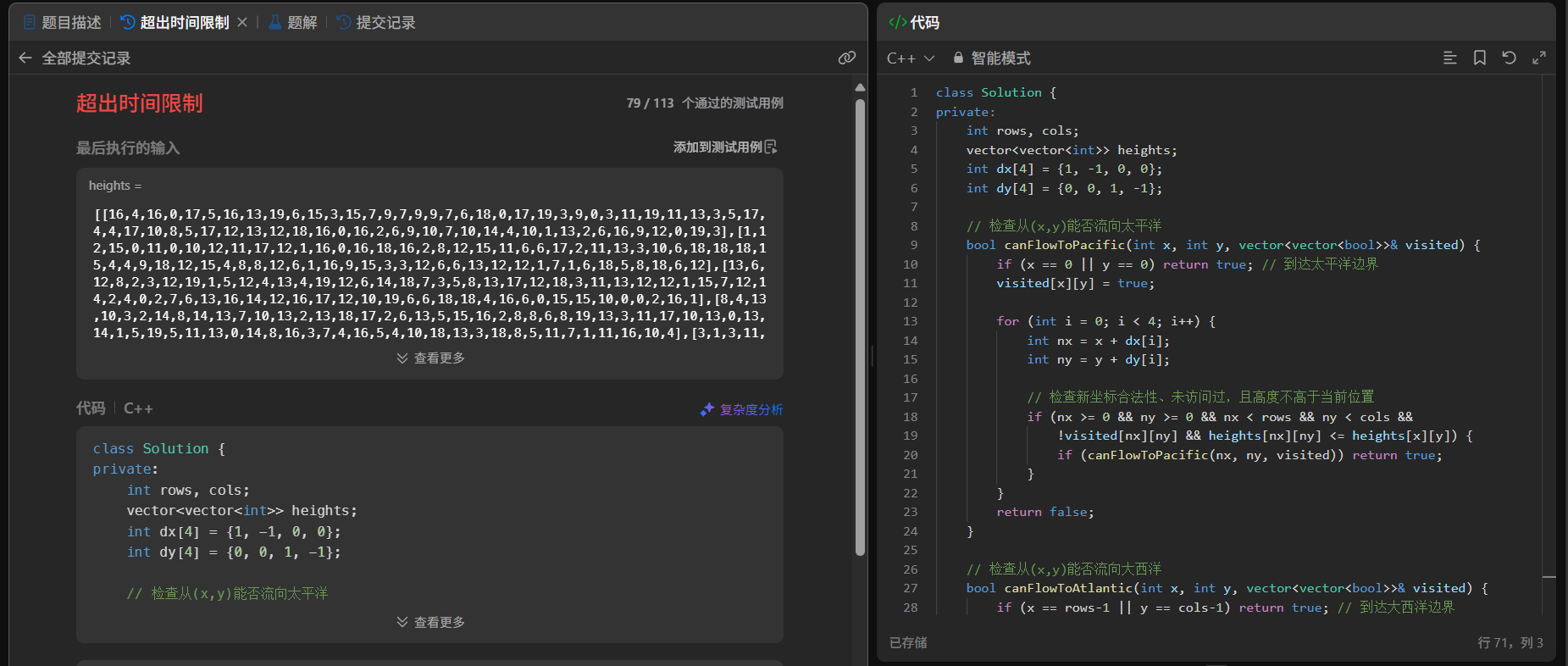
在这里插入图片描述
所以说我们要换一个思路👇

三、正难则反：反向思维的巧妙应用 🔄

既然从格子往海洋流不好算，那咱们反过来想：从海洋往陆地“爬”！

核心逻辑：

太平洋的范围：从所有能直接流入太平洋的边界（上边界 i=0、左边界 j=0）出发，标记所有能逆流到达的格子（即这些格子的水可以流到太平洋）。
大西洋的范围：从所有能直接流入大西洋的边界（下边界 i=rows-1、右边界 j=cols-1）出发，标记所有能逆流到达的格子（即这些格子的水可以流到大西洋）。
结果：要是我们遍历完这两个范围那么两个范围的重叠区域，就是既能流到太平洋又能流到大西洋的格子！

生动比喻 🌊➡️🏔️：
想象太平洋和大西洋的水在涨潮，水可以往高处漫（和自然规律相反，这里是“逆水行舟”）。最终，被两边的水都淹没的地方，就是我们要找的答案～

步骤拆解：

第一步：用 Pmark 数组标记太平洋能“淹到”的格子
- 从 (0,j)（上边界）和 (i,0)（左边界）开始DFS
- 只有当相邻格子更高或等高时，水才能漫过去
第二步：用 Amark 数组标记大西洋能“淹到”的格子
- 从 (rows-1,j)（下边界）和 (i,cols-1)（右边界）开始DFS
第三步：遍历所有格子，同时被 Pmark 和 Amark 标记的就是结果

（思考时间！）💡

理解了“正难则反”的思路后，不妨先自己动手试试写代码？

如何初始化两个标记数组？
DFS的递归条件应该怎么写？
如何高效求两个标记数组的交集？

先尝试独立实现，再看下面的代码解析，收获会更大哦～

四、代码实现：一步步拆解

class Solution {
public:// 方向数组：上下左右（顺序不影响，覆盖四个方向即可）int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int rows, cols; // 网格的行数和列数vector<vector<int>> result; // 存储最终结果vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {// 边界检查：空网格直接返回if (heights.empty() || heights[0].empty()) return result;rows = heights.size();cols = heights[0].size();// 初始化标记数组：记录能流到两个海洋的格子vector<vector<bool>> Pmark(rows, vector<bool>(cols, false)); // 太平洋vector<vector<bool>> Amark(rows, vector<bool>(cols, false)); // 大西洋// 1. 标记太平洋的范围// 左边界（j=0）的所有格子for(int i = 0; i < rows; i++) {dfs(i, 0, heights, Pmark);}// 上边界（i=0）的所有格子（注意：(0,0)已经被左边界处理过，这里会重复调用但不影响）for(int j = 0; j < cols; j++) {dfs(0, j, heights, Pmark);}// 2. 标记大西洋的范围// 右边界（j=cols-1）的所有格子for(int i = 0; i < rows; i++) {dfs(i, cols-1, heights, Amark);}// 下边界（i=rows-1）的所有格子for(int j = 0; j < cols; j++) {dfs(rows-1, j, heights, Amark);}// 3. 找两个范围的交集for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {if(Pmark[i][j] && Amark[i][j]) {result.push_back({i, j});}}}return result;}// DFS函数：从(x,y)出发，标记所有能被当前海洋"淹没"的格子void dfs(int x, int y, vector<vector<int>>& heights, vector<vector<bool>>& mark) {// 1. 如果已经标记过，直接返回（避免重复递归）if (mark[x][y]) return;// 2. 标记当前格子为可到达mark[x][y] = true;// 3. 遍历四个方向，检查能否逆流而上（往高处漫）for(int i = 0; i < 4; i++) {int nx = x + dx[i]; // 新行坐标int ny = y + dy[i]; // 新列坐标// 边界检查：新坐标必须在网格内if(nx >= 0 && ny >= 0 && nx < rows && ny < cols) {// 核心条件：相邻格子比当前高或相等，且未被标记if (!mark[nx][ny] && heights[nx][ny] >= heights[x][y]) {dfs(nx, ny, heights, mark);}}}}
};

代码细节解释：

方向数组：dx 和 dy 定义了上下左右四个方向，避免手写四次重复代码。
标记数组：
- Pmark[i][j] = true 表示 (i,j) 的水可以流到太平洋
- Amark[i][j] = true 表示 (i,j) 的水可以流到大西洋
DFS 触发时机：
- 太平洋从 上边界（i=0） 和 左边界（j=0） 开始
- 大西洋从 下边界（i=rows-1） 和 右边界（j=cols-1） 开始
- 重复触发（如 (0,0) 被两个边界触发）不影响，因为 mark[x][y] 会过滤重复
DFS 核心逻辑：
- 先标记当前格子为“可到达”
- 对四个方向的邻居，只有当 邻居更高或等高 且 未被标记 时，才递归深入
- 这模拟了“水往高处漫”的逆向过程
结果收集：两个标记数组都为 true 的格子，就是既能流到太平洋又能流到大西洋的目标。

代码拆解:

1. 类中成员变量解析

class Solution {
public:// 方向数组：上下左右四个方向的坐标偏移，避免重复写坐标计算int dx[4] = {1, -1, 0, 0};  int dy[4] = {0, 0, 1, -1};  int rows, cols;  // 存储网格的行数、列数，dfs 中直接复用vector<vector<int>> result;  // 最终结果：同时流向两大洋的坐标
};

作用：

把重复用的变量（方向、网格尺寸）设为类成员，减少函数传参，让代码更简洁。
result 集中存结果，避免分散处理。

2. 主函数核心逻辑

vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {// 边界防护：空网格直接返回if (heights.empty() || heights[0].empty()) return result;  rows = heights.size();  cols = heights[0].size();  // 标记数组：记录能流向太平洋、大西洋的格子vector<vector<bool>> Pmark(rows, vector<bool>(cols, false));  vector<vector<bool>> Amark(rows, vector<bool>(cols, false));  // 1. 从太平洋边界启动 DFS（上边界 + 左边界）for (int i = 0; i < rows; i++) dfs(i, 0, heights, Pmark);   // 左边界for (int j = 0; j < cols; j++) dfs(0, j, heights, Pmark);   // 上边界  // 2. 从大西洋边界启动 DFS（下边界 + 右边界）for (int i = 0; i < rows; i++) dfs(i, cols-1, heights, Amark); // 右边界for (int j = 0; j < cols; j++) dfs(rows-1, j, heights, Amark); // 下边界  // 3. 找交集：同时被两个海洋标记的格子for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (Pmark[i][j] && Amark[i][j]) {result.push_back({i, j});  }}}return result;
}

核心步骤：

边界防护：先判空，避免后续越界访问。
标记数组：Pmark 记能流太平洋的格子，Amark 记能流大西洋的格子。
逆向 DFS：从海洋边界（太平洋上/左、大西洋下/右）往陆地 “逆流”，标记所有能连通的格子。
找交集：同时被 Pmark 和 Amark 标记的格子，就是答案。

3. DFS 函数核心逻辑

void dfs(int x, int y, vector<vector<int>>& heights, vector<vector<bool>>& mark) {// 已标记过就跳过，避免重复递归if (mark[x][y]) return;  mark[x][y] = true;  // 标记当前格子为“可流向对应海洋”// 遍历四个方向for (int i = 0; i < 4; i++) {  int nx = x + dx[i];  // 新行坐标int ny = y + dy[i];  // 新列坐标// 检查：新坐标合法 + 未标记 + 高度 >= 当前（逆流条件）if (nx >= 0 && ny >= 0 && nx < rows && ny < cols && !mark[nx][ny] && heights[nx][ny] >= heights[x][y]) {dfs(nx, ny, heights, mark);  // 递归标记相邻格子}}
}

核心设计：

标记优先：进入 DFS 先标记当前格子，避免重复处理。
逆流逻辑：只有相邻格子高度 >= 当前（模拟 “水往高处漫”），才递归（和自然水流相反，是逆向思维关键）。
边界检查：nx、ny 要在网格内，否则跳过。

4. 局部递归示例（以太平洋左边界 (0,0) 为例）
假设网格如下（简化示意，仅看关键流程）：

heights = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]

触发 dfs(0, 0, heights, Pmark)（太平洋左边界起点），递归过程：

第一步：dfs(0,0)
- 标记 Pmark[0][0] = true
- 检查四个方向：
  - 下（dx[0]=1）：nx=1, ny=0 → 高度 4 >= 1 → 递归 dfs(1,0)
  - 上、左：越界或已处理，跳过
  - 右：需等待 dfs(1,0) 及其所有递归分支执行完毕并回溯后，才会处理 (0,1)。
第二步：dfs(1,0)
- 标记 Pmark[1][0] = true
- 检查四个方向：
  - 下（nx=2, ny=0）：高度 7 >= 4 → 递归 dfs(2,0)
  - 上（nx=0, ny=0）：已标记，跳过
  - 右（nx=1, ny=1）：高度 5 >= 4 → 递归 dfs(1,1)
  - 左：越界，跳过
第三步：dfs(2,0)、dfs(1,1) 继续扩散…
- 最终，所有能从 (0,0) 逆流到达的格子都会被标记为 Pmark = true，模拟 “太平洋的水往陆地漫” 的过程。

递归特点：像 “逆向洪水”，从海洋边界出发，逐步标记所有能连通的陆地，直到无法再逆流为止。

总结
代码通过 逆向 DFS（从海洋往陆地流） + 双标记数组（太平洋/大西洋） + 交集筛选，高效解决了 “判断水流双向连通” 的问题。类成员变量简化了传参，DFS 递归实现了 “逆流标记”，主函数通过边界遍历 + 交集计算，最终得到结果。

结合示例模拟递归流程，能更直观理解 “逆向思维 + 洪水灌溉” 的巧妙用法～

时间复杂度分析

核心逻辑：算法通过两次独立的 DFS 遍历（分别对应太平洋和大西洋）标记所有可达格子，最终计算交集。
具体计算：
- 网格共有 m*n 个格子（m 为行数，n 为列数）。
- 每个格子最多被 2 次 DFS 访问（太平洋遍历一次，大西洋遍历一次）。
- 每次 DFS 中，每个格子的处理（检查方向、标记）是常数时间 O(1)。
结论：总时间复杂度为 O(m*n)，与网格规模线性相关，效率高效。

空间复杂度分析

核心消耗：主要来自两部分——递归调用栈和标记数组。
具体计算：
- 标记数组：Pmark 和 Amark 各占用 m*n 空间，合计 O(m*n)。
- 递归栈：最坏情况下（如网格是递增序列，DFS 需遍历所有格子），递归深度可达 m*n（例如从边界一直递归到对角），占用 O(m*n) 空间。
结论：总空间复杂度为 O(m*n)，由标记数组和递归栈共同决定。