们先来回想一件事,根据欧姆定律,阻抗是不是越低越好? 代表即使有很大的瞬时电流,瞬间的电压降也不会超过某个极限!
理论上是! 可是这其实忽略了两个关键的要素:
- PDN阻抗有谐振:谐振代表能量的快速转换,即便这个谐振是属于往下掉的串联谐振,还是有可能引发能量的高度震荡
- 电源波形有频率成分:如果电源波形的频率刚好跟谐振频率对齐,那会引发PDN网络有剧烈的噪声震荡
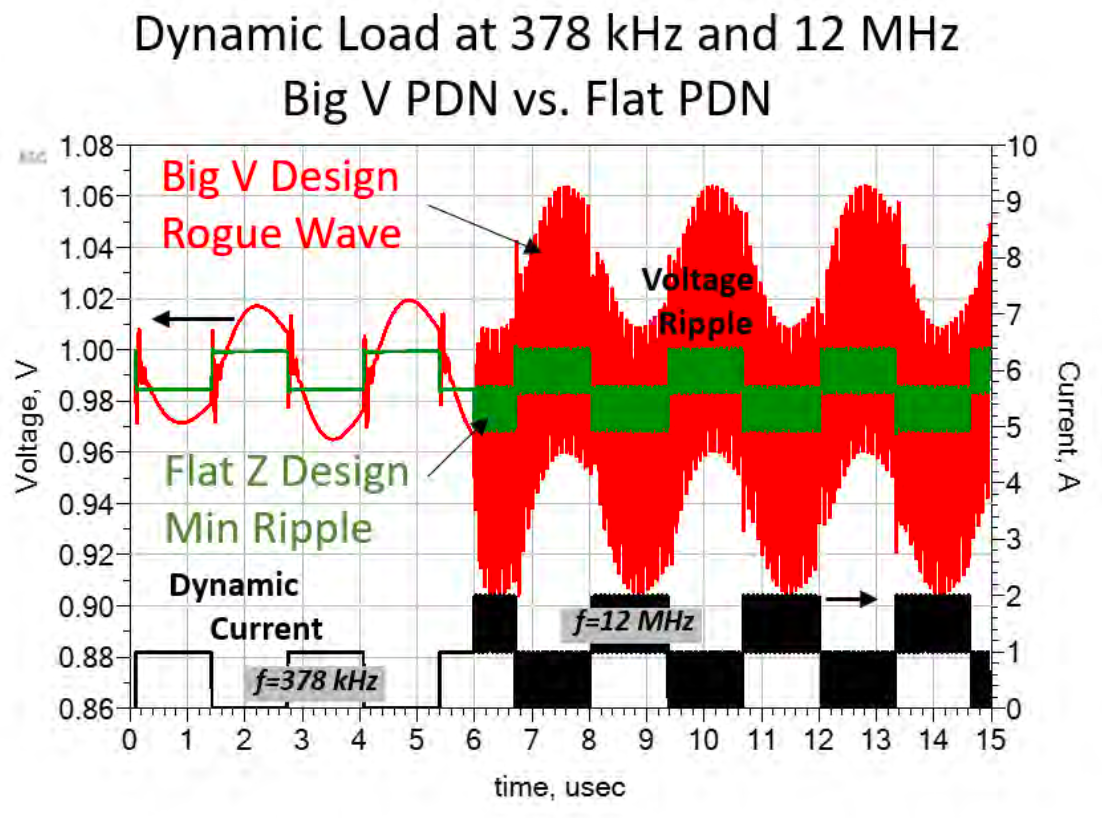
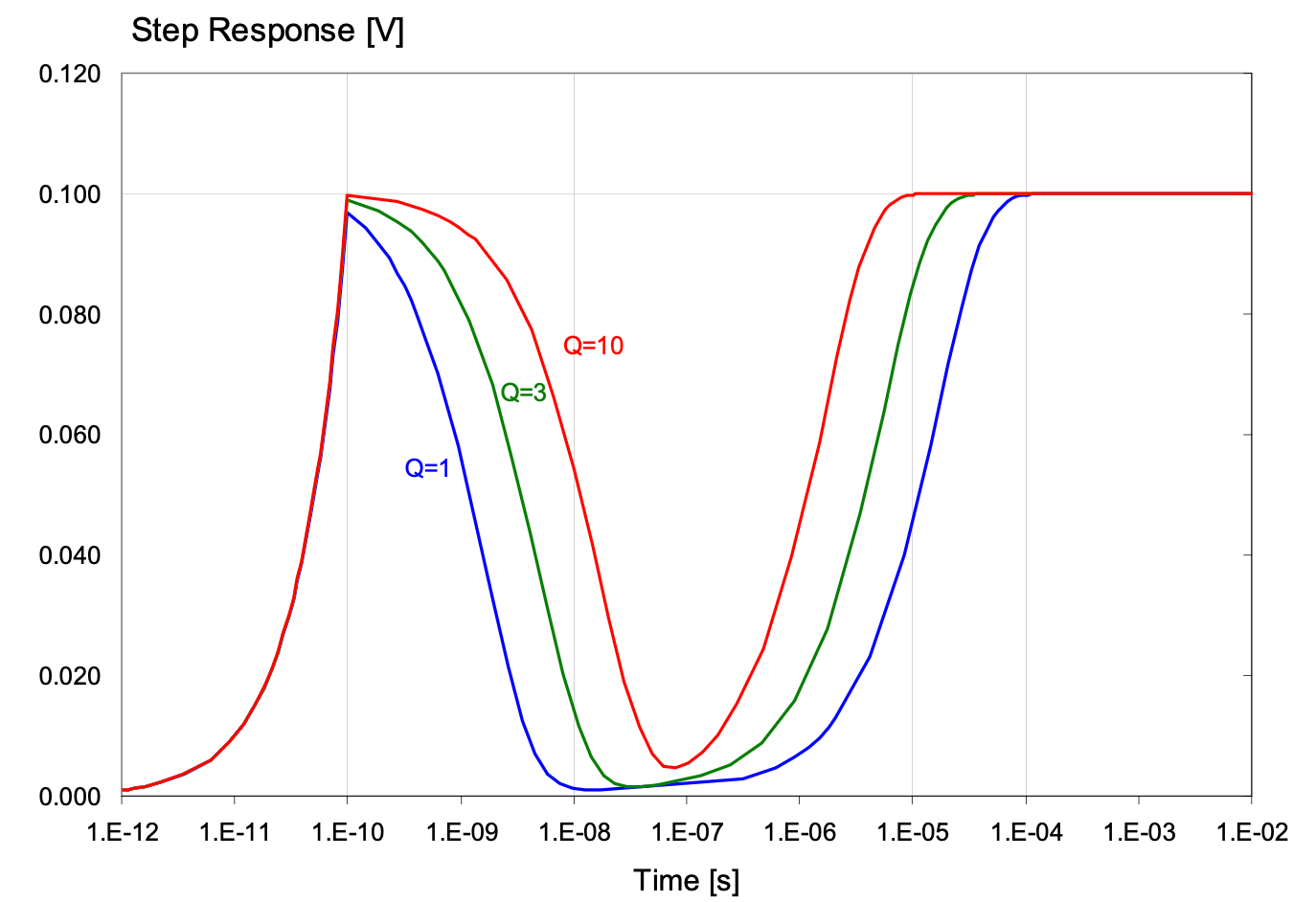
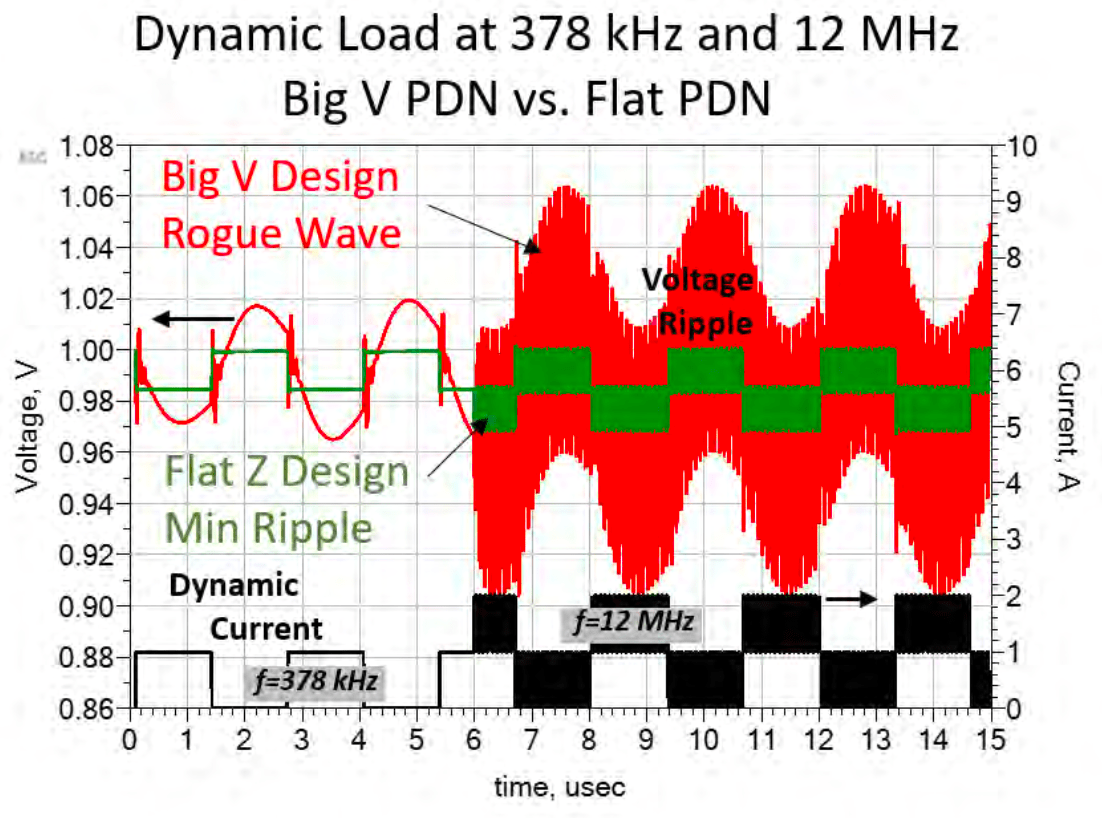
就如同下面这个案例所示,我们可以观察到一个非常明显的现象:一个串联谐振确实将整体阻抗往下拉,乍看之下这似乎是个大多数设计者希望达到的的状态,开心地很。 然而,当我们进一步测试并输入一个步阶响应(Step Response)作为电流源抽载后,结果令人意外,我们发现电压产生了极为剧烈的震荡现象。 在这个特定案例中,震荡幅度高达100mV,虽然这个数值可能是比较夸张的例子,但它确实揭示了一个关键问题:这样的结果是否已经彻底颠覆了“阻抗越低越好”这个在PI领域中普遍被接受的设计认知? 这个现象值得我们深入思考,重新审视我们对PDN设计的基本假设。
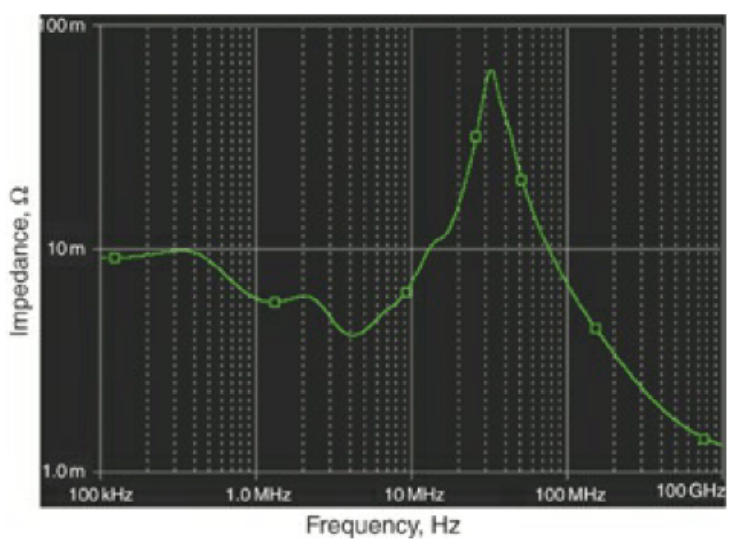
或是如果有在100MHz这个区域甚至更高的频率有超过Target impedance的反谐振点,就很有可能引发所谓Rogue Wave的大海啸,电压波形会开始唱世界名曲,炸裂...
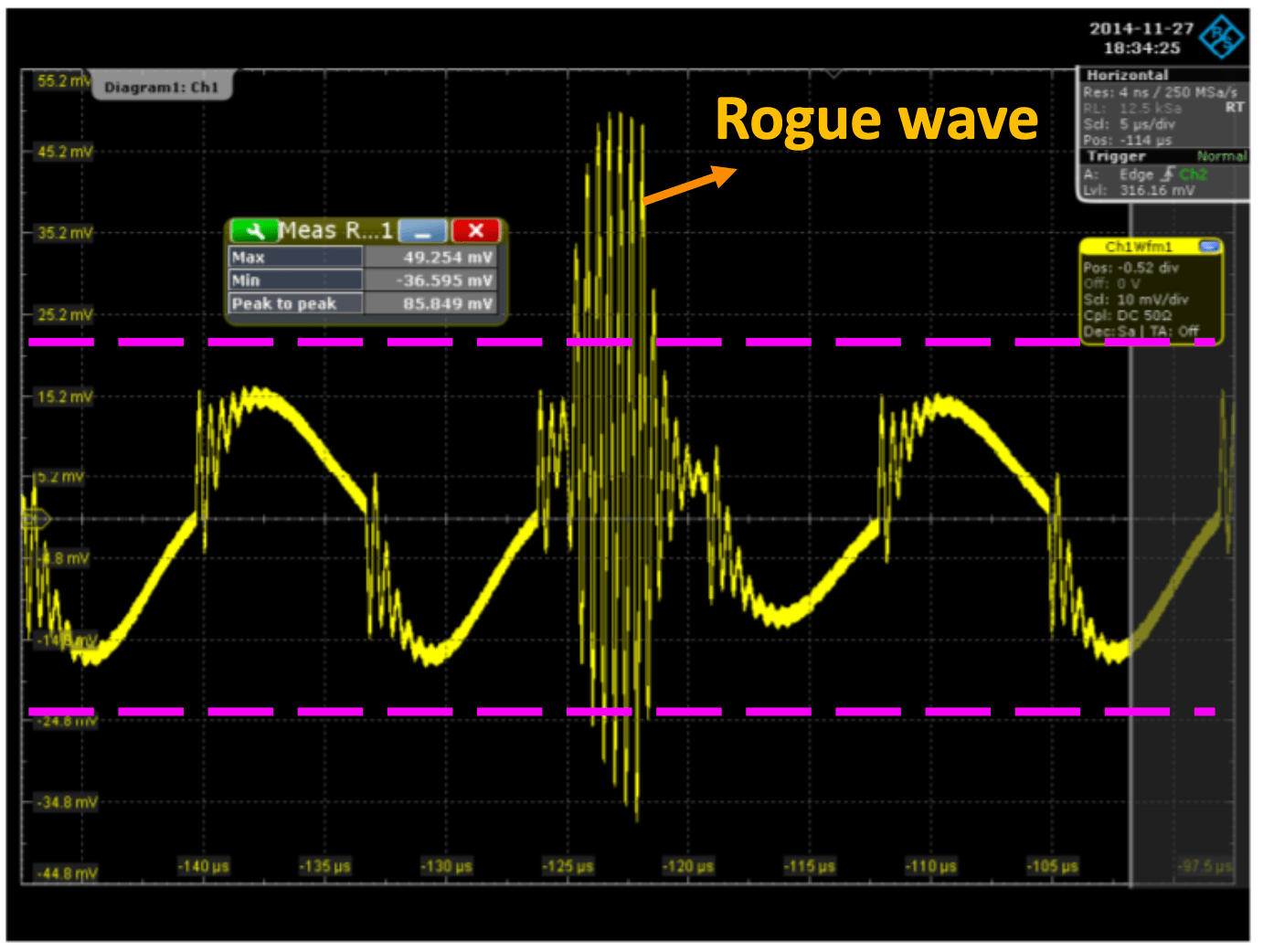
震荡的万恶起源 – 谐振
谐振(Resonance)是一种物理现象,指一个物理系统在受到周期性外部激励时,若外部激励的频率与该系统的自然频率(Natural Frequency)相匹配或非常接近,系统将会产生极其剧烈的响应,例如振幅的急剧增大 。 此一特定频率被称为谐振频率(Resonant Frequency)。
以上这段是我问AI的,基本上大自然间各种结构都存在着谐振,也就是在这个频率点被激发后,能量会大量爆发出来,产生噪声、干扰,影响可以很巨大!
在电路板中,这些谐振大多数由寄生电容与寄生电感造成,电容是储存电能的元器件,电感则是用来储存磁能,当这两者在某一频率产生谐振时,电容的电能会转换成磁能丢给电感,电感的磁能则会转化成电能丢给电容,如果有人在这个频率点打破这个交换的平衡,则会引爆巨大的能量。
在PI领域中,谐振我们又可以将其分成这两种:
- 串联谐振
- 并联谐振
有何差异呢?
电容与电感
首先,我们先来看电容与电感这两个基本元器件的阻抗随频率变化的关系。
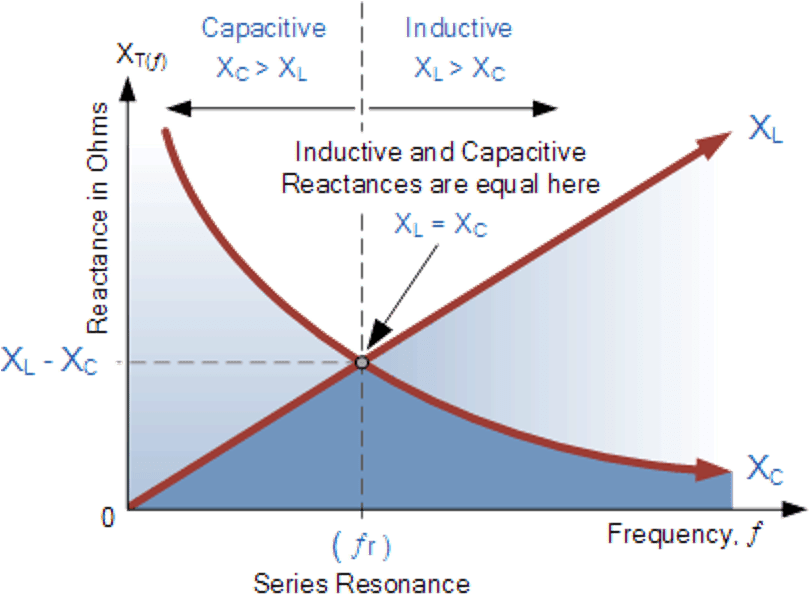
电容的阻抗随频率变高会降低,而电感的阻抗会随着频率变高而变大。
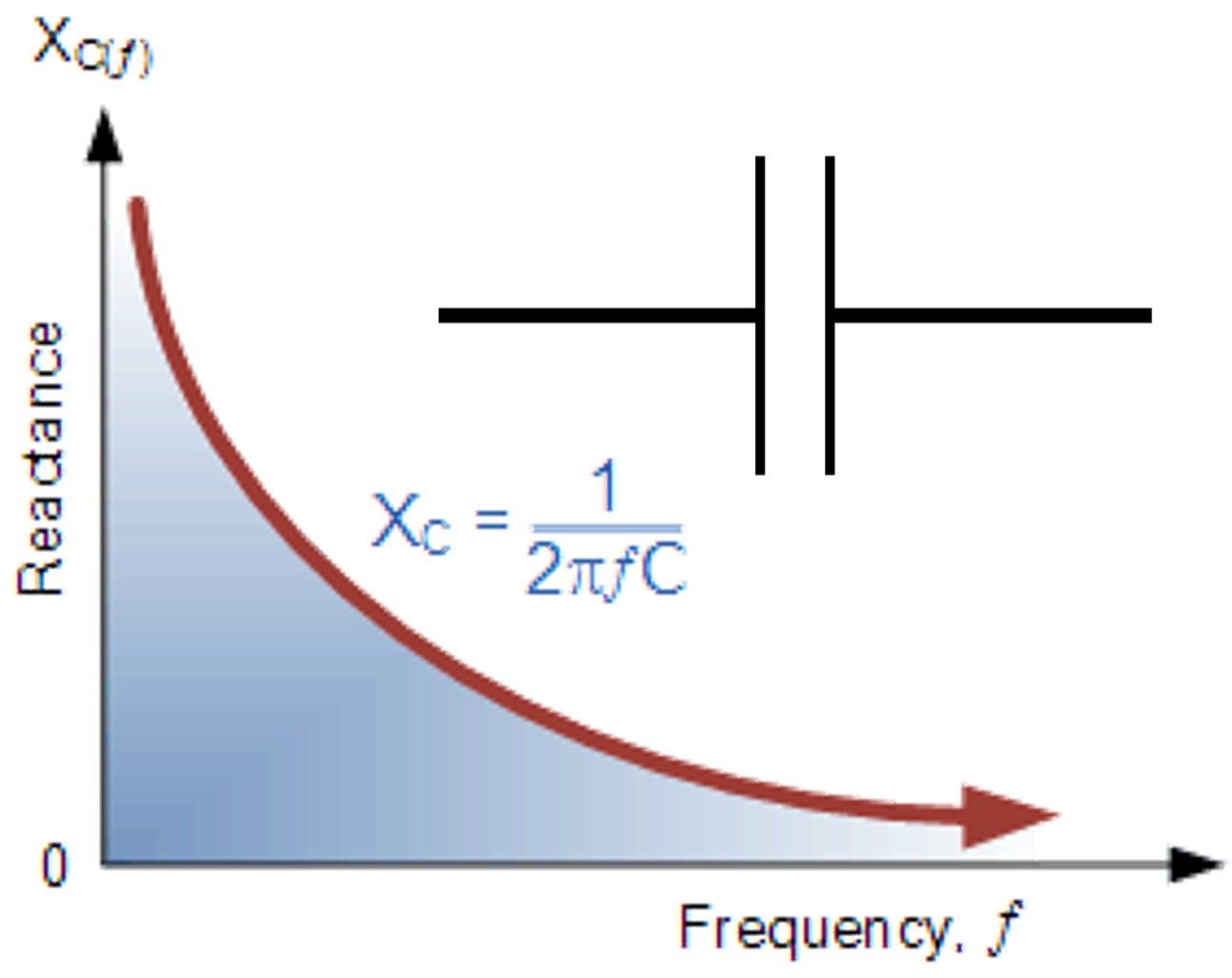
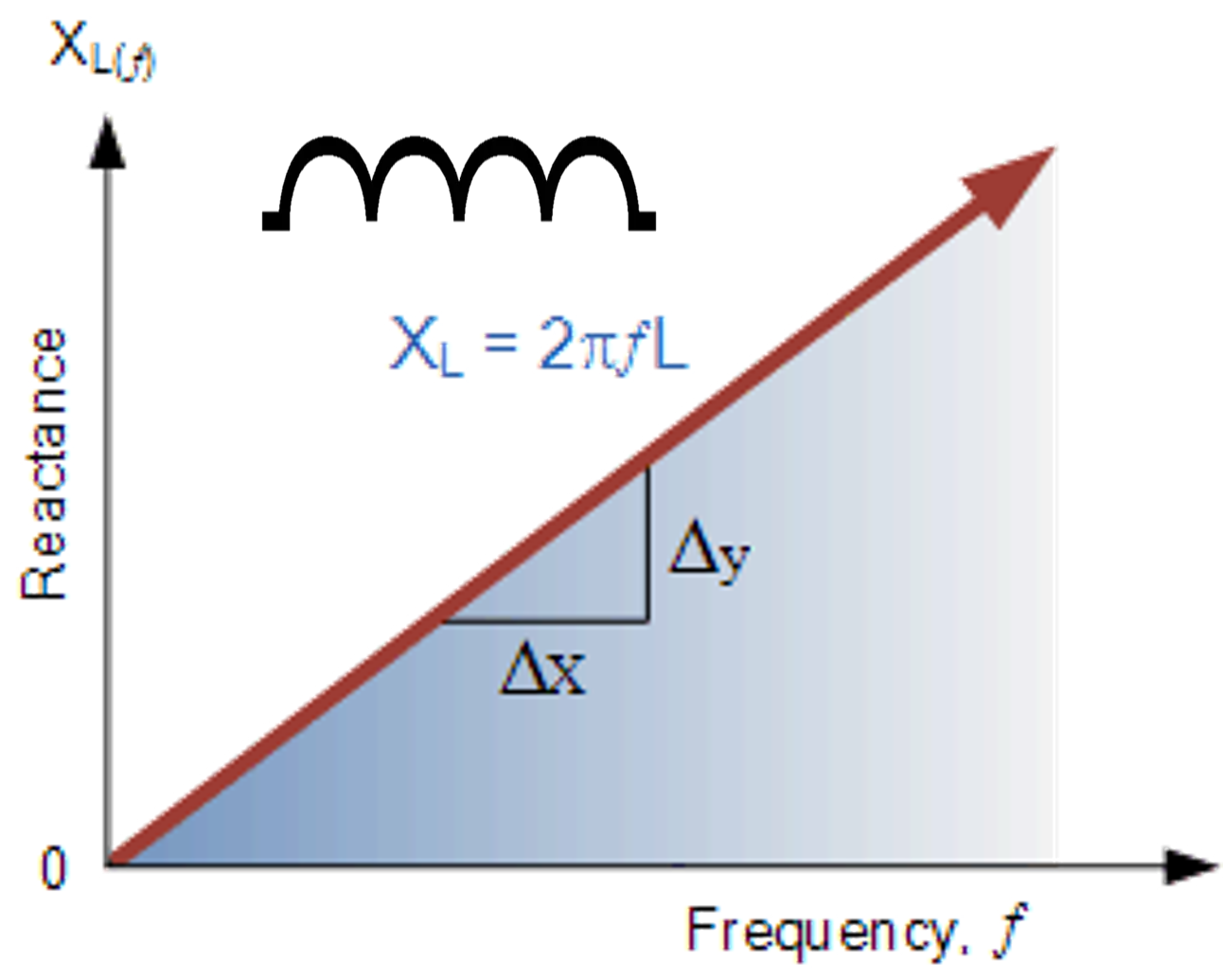
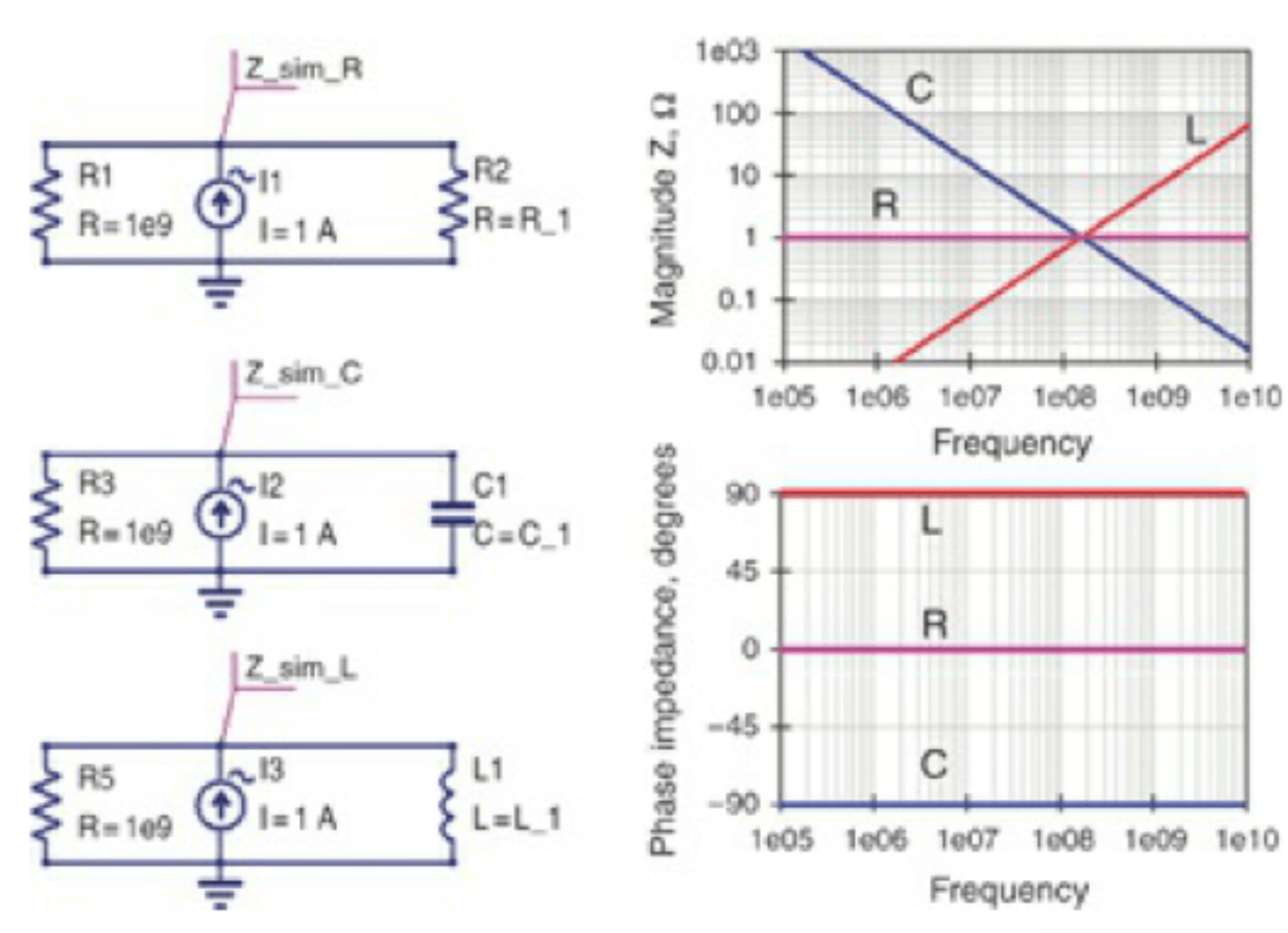
这边说的是理想的电容与电感,如果是现实中我们在使用的电容器件如MLCC(Multi-Layered Ceramic Capacitor)、Film Capacitor、Polymer等等; 而电感器件,像是Choke或是Ferrite bead等等都会有寄生的杂散效应,所以阻抗曲线就不是完全符合这条曲线。
像是这颗Murata的22nF电容,就会有串联谐振点,过了这个谐振点,电容器件就会转换成电感特性,也就是说... 电容某种程度上其实可以当做电感用... 只是... 麦阿捏啦!
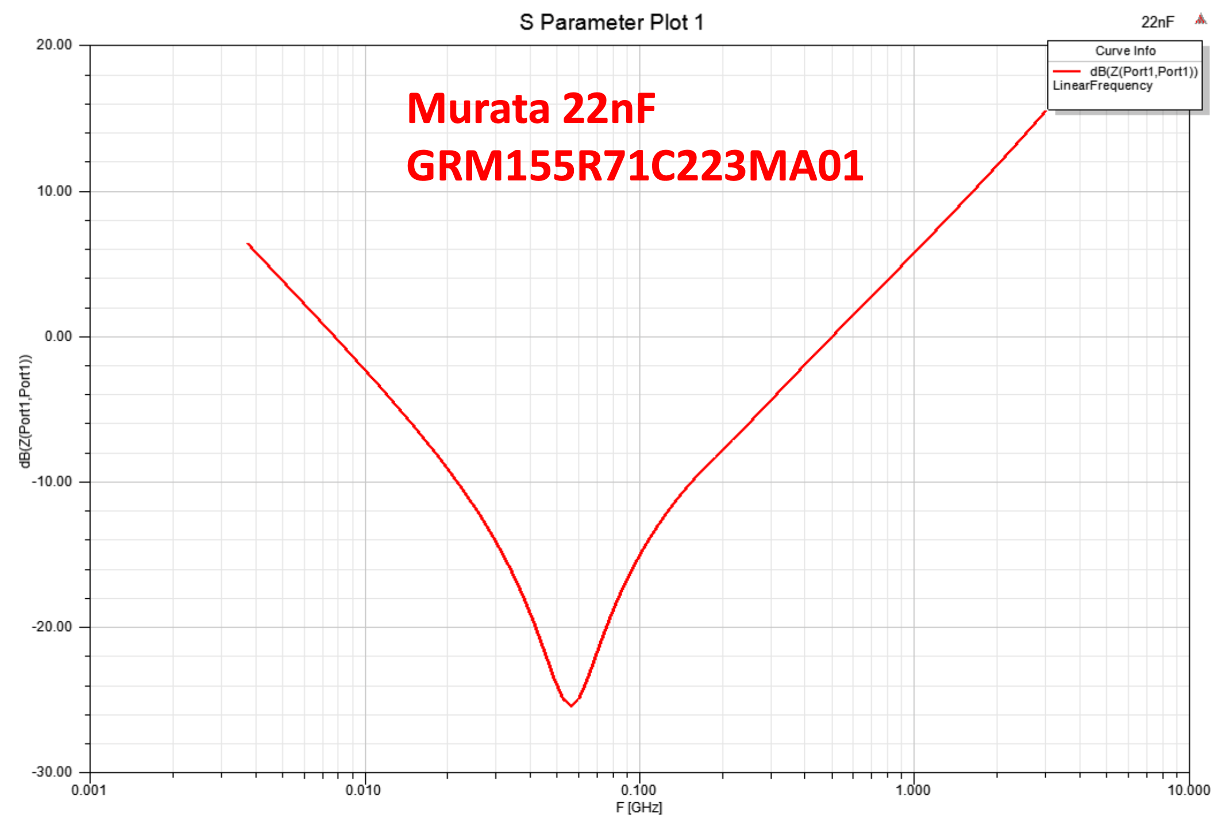
串联谐振(Series Resonance)
各位可以先记得,谐振产生的频率点,就是电容抗跟电感抗两者相交叉的那个点。
也就是电感抗=电容抗:
XL=XCXL=XC
而一个RLC串联电路的系统阻抗可以写成:
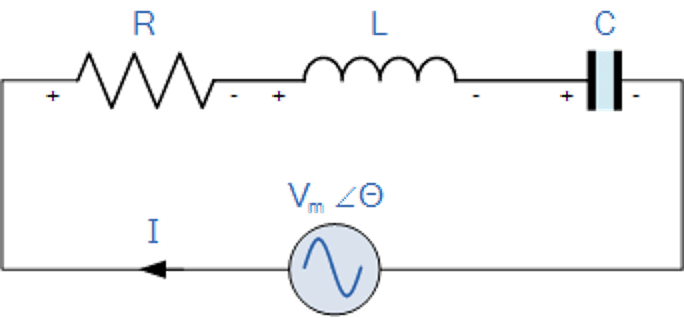
ZRLC=RDC+ZL+ZCZRLC=RDC+ZL+ZC
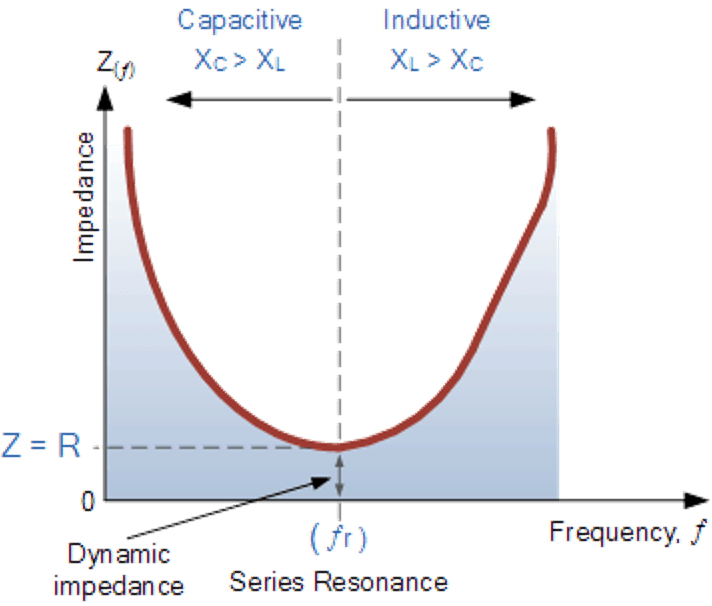
在谐振点时,电路的总电抗为0(XL=-XC),代表整个电路只剩下RDC。 对,没错,电感跟电容在谐振频率上会消失。
基本逻辑是这样,在串联电路上低频的表现由开路电路来主导,而电容低频属于高阻抗(开路Open),所以可以看到低频时阻抗曲线在左上角。 而随着频率越来越高,电容抗会下降,电感抗会跑出来,两条曲线会交叉在一起,这个就是谐振频,这是整个电路剩下电阻。 再往更高频走,电容阻抗持续下降,电感阻抗继续攀升,就会变成整个阻抗曲线像个V字型!
串联谐振会有V字体的阻抗曲线:
这个频率点可以通过以下公式计算:
f=12πLCf=2πLC1
也就是说,当电感与电容越大,谐振频就越低; 反之,这两者变小时,谐振频就越高。
我们可以藉由调整电容与电感来看阻抗曲线的变化,当电容变大时(1nF → 100nF),低频阻抗变小,谐振频跑到低频,高频阻抗不变。
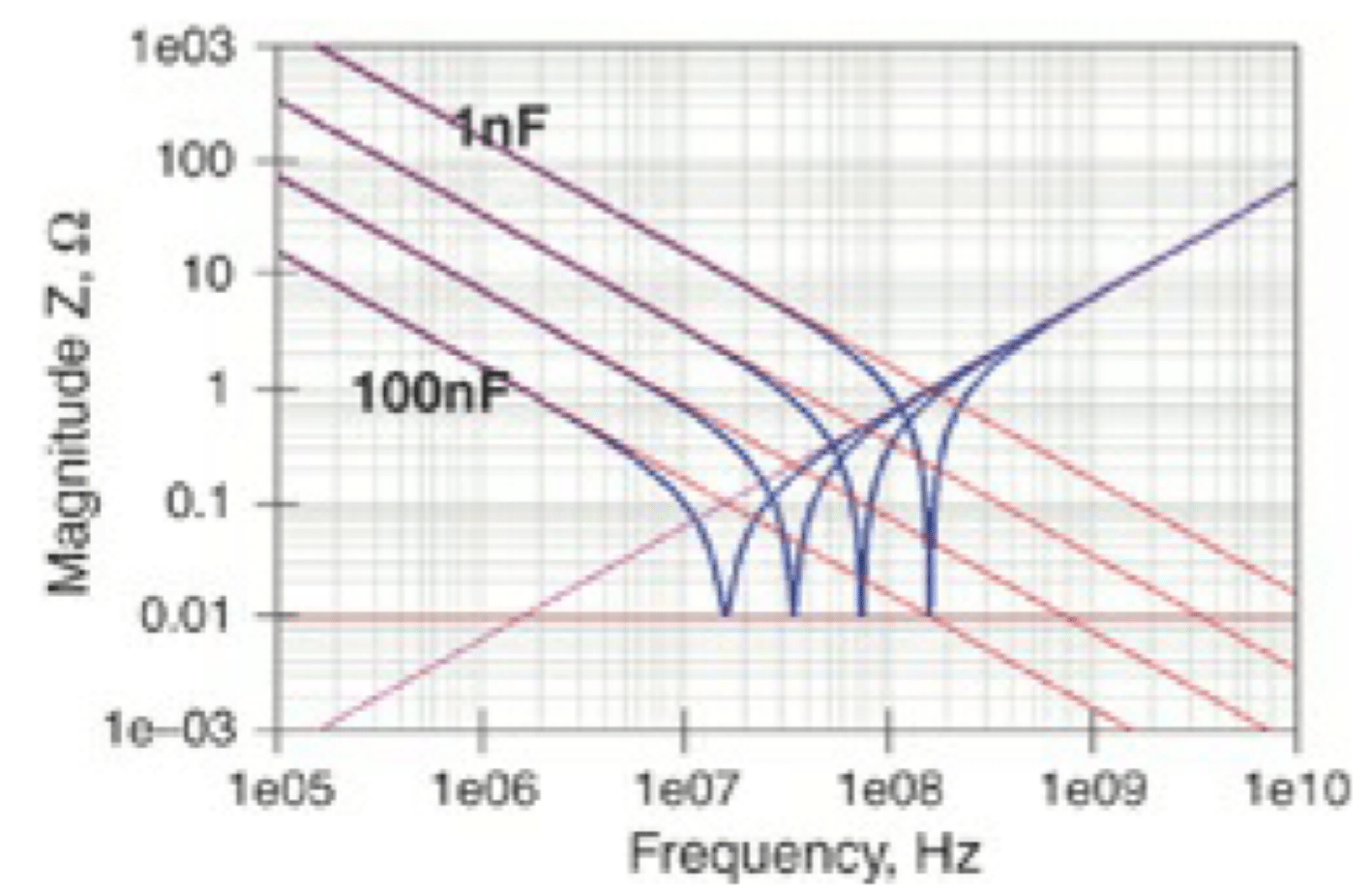
而当电感变大时(1nH → 100nH),低频阻抗不变,高频阻抗变大,谐振频往低频跑。
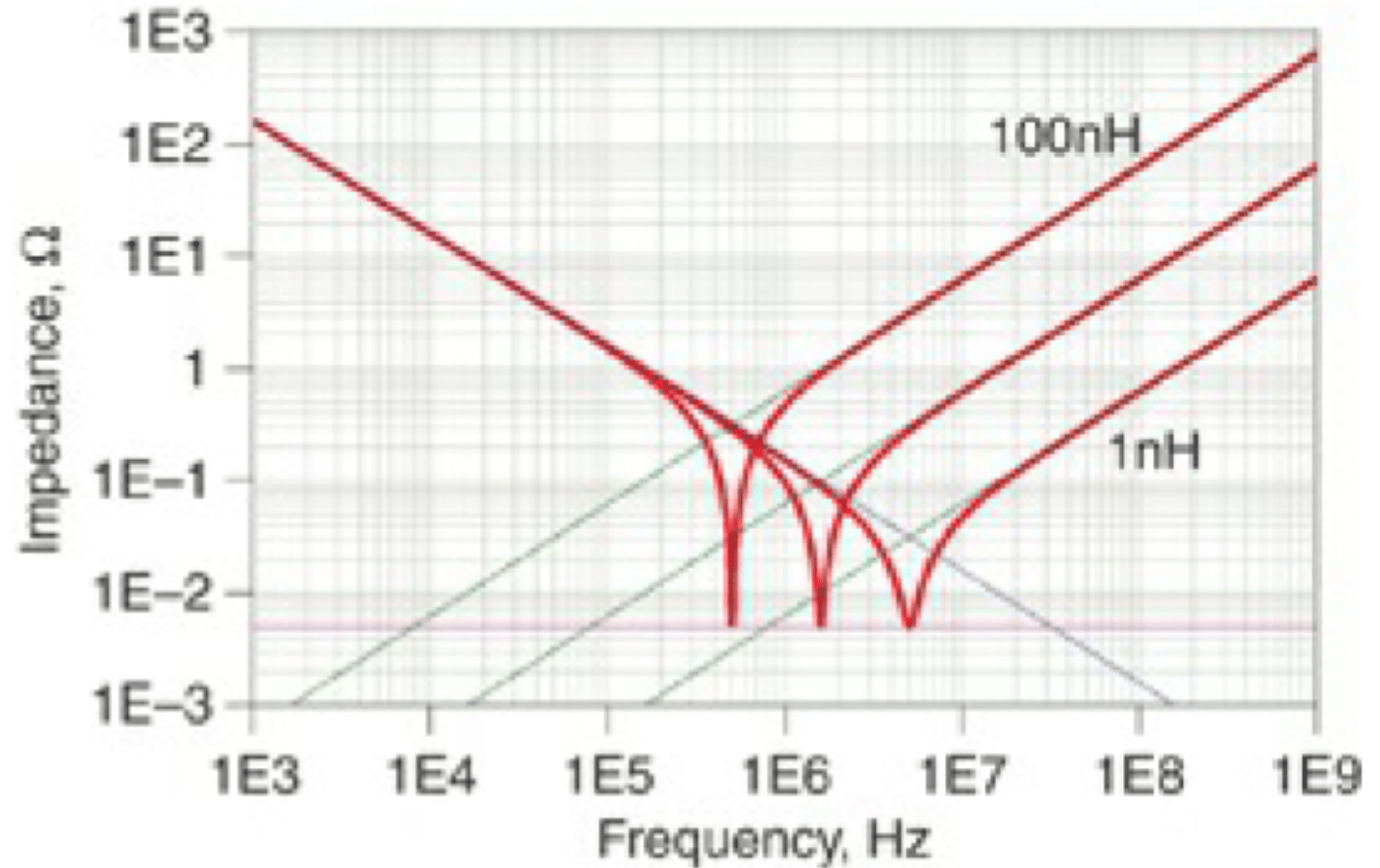
通常这种谐振的代表就是电容器,因为可以串联谐振可以拉低整个电源阻抗,所以我们才会使用MLCC这类型的电容来解决阻抗问题。
并联谐振(Parallel Resonance)
当RLC并联时,电路可以画成:
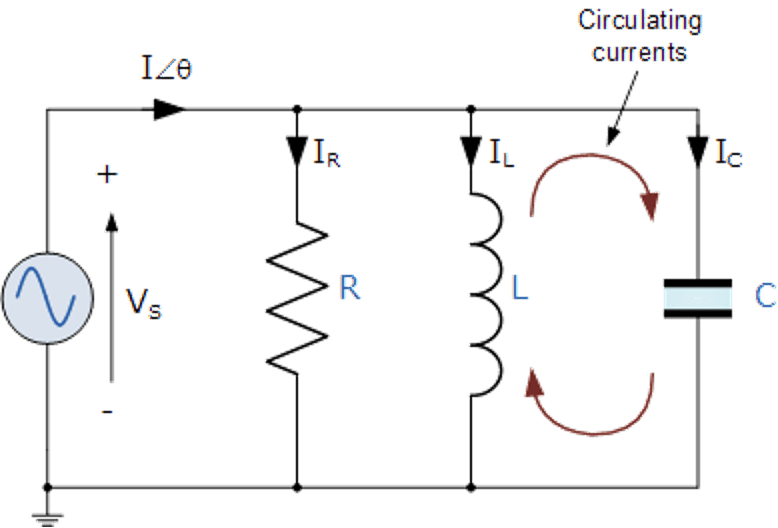
系统阻抗可以用导纳Y表示:
Y=1R+1jwL+jwCY=R1+jwL1+jwC
低频的阻抗由电感主导,阻抗随着频率变大而增加; 当电容抗与电感抗相同时,这个频率点为谐振点,为高阻抗。 在更高频,阻抗又再度被电容在高频时的低阻抗给拉下来,呈现一个倒V字型:
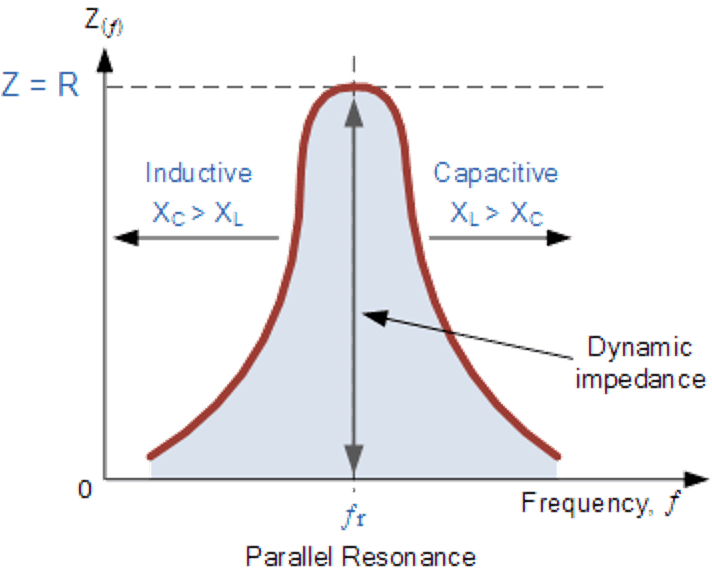
谐振频率点的计算与串联谐振相同:
f=12πLCf=2πLC1
这类型的阻抗,通常发生在两个对象交接处,例如:
- VRM与PCB MLCC合成的效应
- Package与Silicon Die合成时的结果
尤其是Package与Silicon Die,由于这个阻抗会发生在较高频处,通常伴随而来的Noise ripple也会特别大。
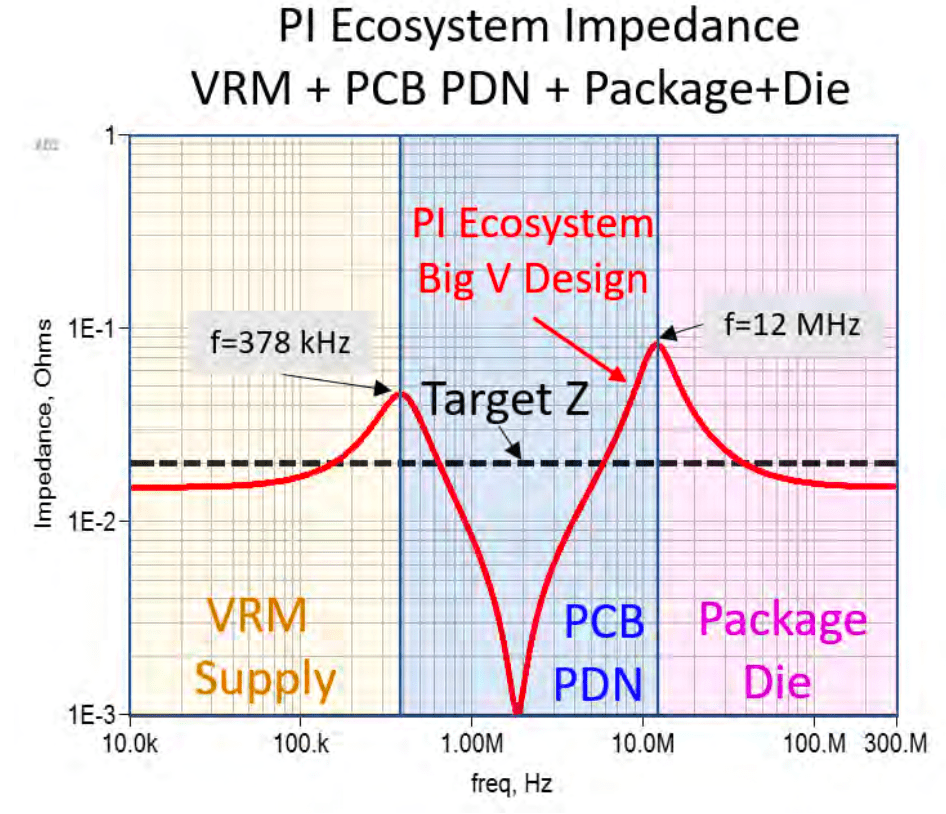
可以看到在378KHz与12MHz都有并联高阻抗谐振,12MHz的电流源造成的Ripple会异常地大。
质量因素 Q-Factor
讲到谐振就一定要讲到Q值。
Q值的最根本定义是,在一个振盪周期内,谐振器中储存的总能量与其消耗的能量之比,再乘以2π。 其数学表达式有两种,第一种是原始定义:
Q=2πEstoredEdissipated/cycleQ=2πEdissipated/cycleEstored
第二种则是透过谐振频率与3dB带宽的比值:
Q=frBWQ=BWfr
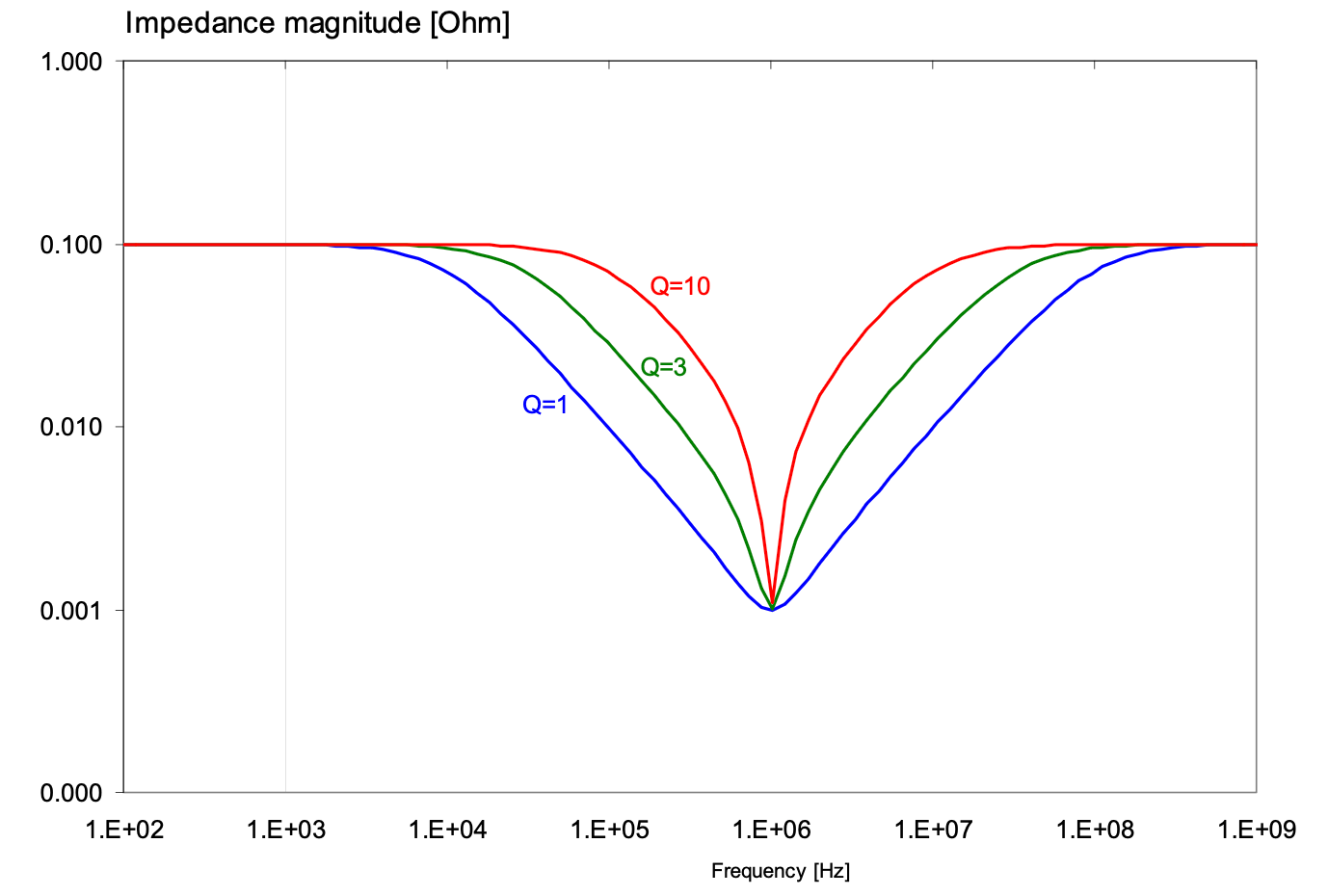
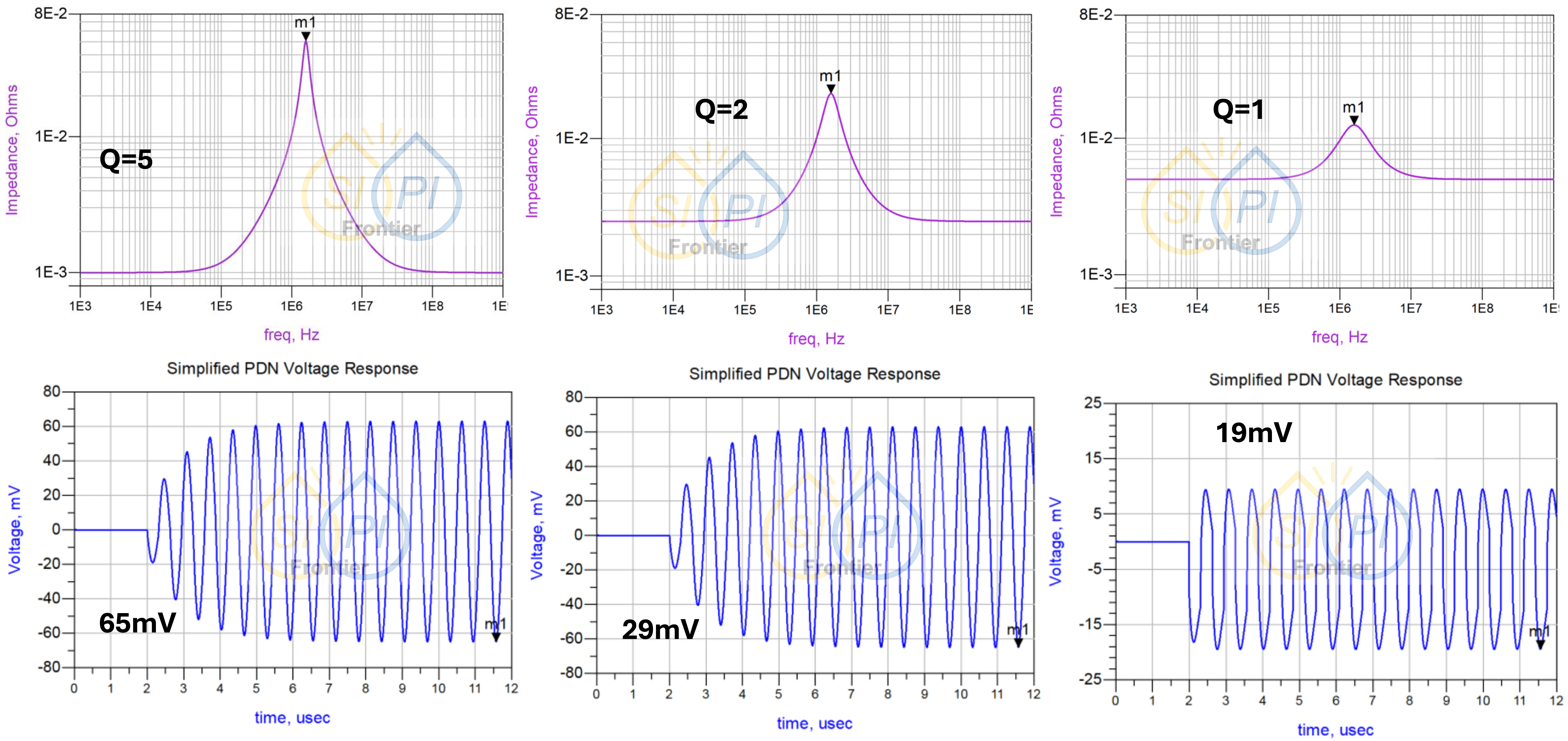
从这个定义可以看出,高Q值意味着谐振器是一个高效的、低损耗的能量储存系统。 But… 对于PI而言不是一个好系统... 因为对于PI而言,我们要的是一个就算有个电流源的频率刚好打到谐振频率,就算真的有一个可能性的电压震荡,这个震荡的能量也可以被迅速消散。 对于高Q值电路而言,阻抗峰值高且尖锐,能量储存较大,没有足够的电阻可以消散能量,一被激发就难以收拾。
所以我们会希望PI设计者可以尽量朝低Q值电路去做设计,代表电阻较大,吃掉这些可能爆发的能量!
从这些结果可以看出,Q值越低,Ripple越小,代表PI设计更好!
)





的花店系统)


?)







)

