论文地址：pdf
代码地址：code

---

1.研究背景与动机

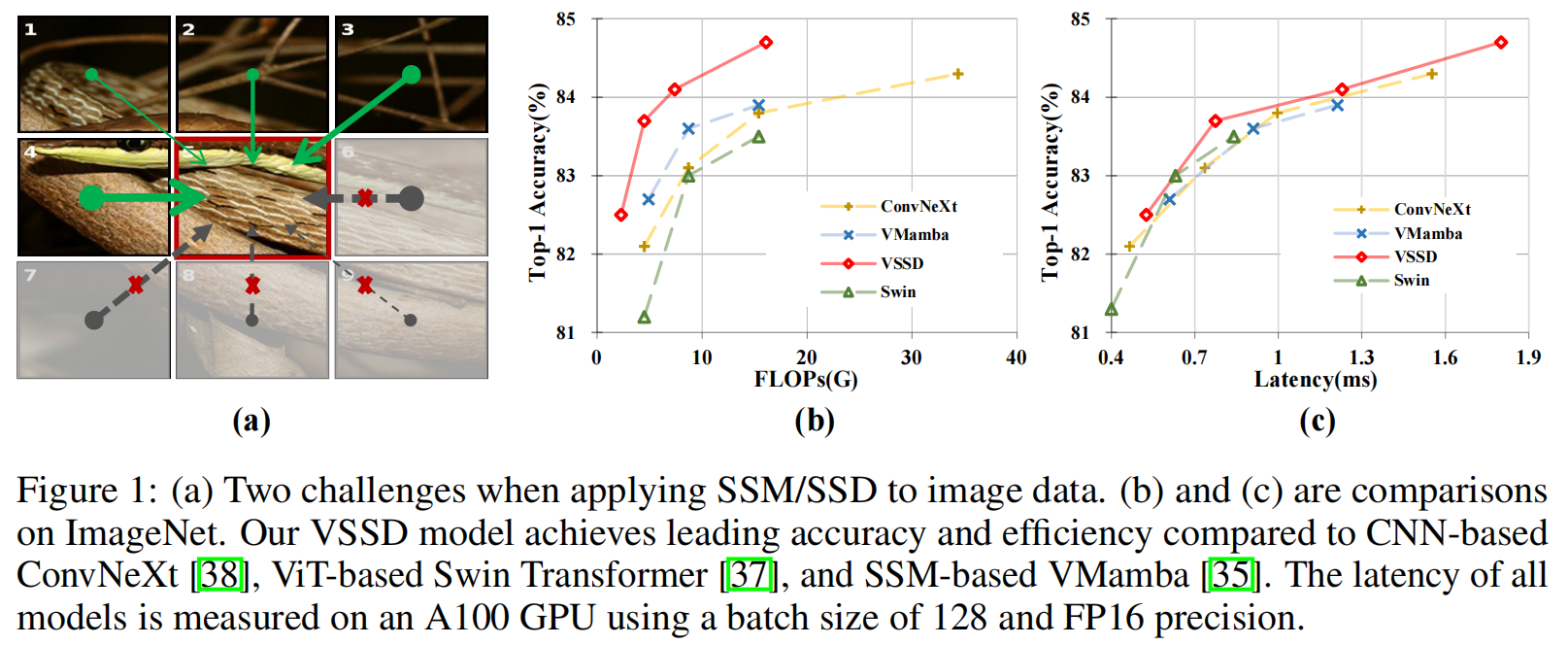
视觉 Transformer 虽凭借全局感受野和强大建模能力在计算机视觉领域取得成功，但其自注意力机制的二次计算复杂度限制了长序列处理能力。状态空间模型（SSMs）如 Mamba 因线性复杂度成为替代方案，但 SSMs 及改进变体 SSD（State Space Duality）存在固有因果性，与图像数据的非因果性矛盾，且将 2D 特征图 flatten 为 1D 序列会破坏空间结构关系。为此，提出VSSD（Visual State Space Duality）模型，通过非因果化 SSD 解决上述问题。

---

2. 核心方法

2.1 预备知识:mamba-ssm

状态空间模型:经典的状态空间模型（SSMs）表示一个连续系统，它将输入序列$x(t)\in {\mathbb{R}}^L$映射到 latent 空间表示$h(t)\in {\mathbb{R}}^N$，然后基于该表示预测输出序列$y(t)\in {\mathbb{R}}^L$。从数学上讲，SSM可描述为：
$$\begin{array}{c}{h}^{\prime }(t)=Ah(t)+Bx(t),y(t)=Ch(t)\end{array}$$
其中$A\in {\mathbb{R}}^{N\times N}$、$B\in {\mathbb{R}}^{N\times 1}$和$C\in {\mathbb{R}}^{1\times N}$是可学习参数。

离散化:为了使连续状态空间模型（SSMs）适用于深度学习框架，实现离散化操作至关重要。通过引入时间尺度参数$\Delta \in \mathbb{R}$并采用广泛使用的零阶保持（ZOH）作为离散化规则，可以推导出A和B的离散化版本（分别表示为$\overline{A}$和$\overline{B}$），据此，式1可重写为离散形式：
$$\begin{array}{c}\begin{array}{rl}h(t)& =\overline{A}h(t-1)+\overline{B}x(t),y(t)=Ch(t),\\ \text{where }\overline{A}& =e^{\Delta A},\overline{B}=(\Delta A{)}^{-1}\left(e^{\Delta A}-I\right)\Delta B\approx \Delta B\end{array}\end{array}$$
离散化的详细推导可见这篇文章
其中$I$表示单位矩阵。之后，式2的过程可以通过全局卷积的方式实现：
$$\begin{array}{c}y=x\odot \overline{K},\overline{K}=\left(C\overline{B},C\overline{A}\overline{B},\dots ,C{\overline{A}}^{L-1}\overline{B}\right)\end{array}$$
该式直接迭代带入即可得到
其中$x\in {\mathbb{R}}^{1\times L}$是输入序列，$\overline{K}\in {\mathbb{R}}^{L\times 1}$是卷积核。

选择性状态空间模型：Mamba引入的选择性状态空间$S6$机制使参数$\overline{B}$、$\overline{C}$和$\Delta$依赖于输入，从而提升了基于SSM的模型的性能。在使$\overline{B}$、$\overline{C}$和$\Delta$依赖于输入后，式3中的全局卷积核可重写为：
$$\begin{array}{c}\overline{K}=\left(C_L{\overline{B}}_L,C_L{\overline{A}}_{L-1}{\overline{B}}_{L-1},\dots ,C_L\prod _{i=1}^{L-1}{\overline{A}}_i{\overline{B}}_1\right)\end{array}$$
这种修改解决了先前 SSM 模型 [16, 13] 固有的线性时不变（LTI）特性的局限性，从而提升了 SSMs 的适应性和性能。

2.2 非因果状态空间对偶性

最近，Mamba2引入了状态空间对偶性（SSD），并将矩阵$A$简化为标量。这种选择性状态空间模型（SSMs）的特殊情况可通过线性和二次两种形式实现。不失一般性，选择性状态空间模型的矩阵变换形式表示如下：
$$\begin{array}{c}\begin{array}{rl}y(t)& =\sum _{i=1}^t{C}_t^{\top }{A}_{t:i+1}{B}_{i}x(i),\text{其中 }{A}_{t:i}=\prod _{k=i}^t{A}_k,\\ y& =\text{SSM}(A,B,C)(x)=Fx,\text{其中 }{F}_{ji}=C_j^{\top }{A}_{j:i}{B}_i\end{array}\end{array}$$

当$A_i$简化为标量 时，式5的二次形式可重新表述为：
$$\begin{array}{c}y=Fx=M\cdot \left(C^{T}B\right)x,其中M_{ij}=\{\begin{array}{ll}{A}_{i+1}\times \cdots \times A_j& i>j\\ 1& i=j\\ 0& i<j,\end{array}\end{array}$$
其线性形式表示为：
$$\begin{array}{c}h(t)=A_{t}h(t-1)+B_{t}x(t),y(t)=C_{t}h(t).\end{array}$$

为使SSMs适应图像数据，需先将二维特征图展平为一维token序列，再对其进行顺序处理。由于SSMs的因果特性（每个token只能访问之前的token），信息传播本质上是单向的。这种因果特性在处理非因果图像数据时会导致性能不佳，这一发现已得到先前研究的证实。此外，将二维特征图展平为一维序列会破坏其内在的结构信息。例如，在二维图中相邻的token在一维序列中可能相距甚远，从而导致视觉任务性能下降。由于SSD是SSMs的一种变体，将SSD应用于视觉任务会遇到与SSMs类似的挑战：

• 挑战1：模型的因果特性限制了信息流动，使后续token无法影响先前的token。

• 挑战2：在处理过程中，将二维特征图展平为一维序列会破坏补丁之间固有的结构关系。

在将因果SSD应用于非因果图像数据的背景下，回顾SSD的线性公式很有启发性。在式7中，标量$A_t$调节先前隐藏状态$h(t-1)$和当前时间步信息的影响。换句话说，当前隐藏状态$h(t)$可视为先前隐藏状态和当前输入的线性组合，分别由$A_t$和1加权。因此，如果我们忽略这两项的大小，只保留它们的相对权重，式7可重写为：
$$\begin{array}{c}h(t)=h(t-1)+\frac{1}{A_t}{B}_{t}x(t)=\sum _{i=1}^t\frac{1}{A_i}{B}_{i}x(i).\end{array}$$

在这种情况下，特定token对当前隐藏状态的贡献可由其自身直接通过$\frac{1}{A_i}$确定，而非通过多个系数的累积乘法。由于每个token的贡献具有自参考性，挑战2仅得到部分解决，因为由于挑战1中讨论的问题，当前token只能访问一部分token。

为解决挑战1，先前基于SSM的视觉模型经常采用多扫描路径。具体而言，在ViM中，对token序列进行正向和反向扫描，使每个token能够访问全局信息。尽管这些多扫描方法减轻了SSMs的因果特性，但它们并未解决挑战2，因为SSMs的长程衰减特性仍局限于一维形式，并未扩展到二维。为了能够获取全局信息，从而适应非因果图像数据，我们也从双向扫描策略入手。并且我们证明，正向和反向扫描的结果可以整合起来，以同时有效解决上述两个挑战。令$H_i$表示双向扫描方法中第$i$个token的隐藏状态，由此我们可以很容易地得出：
$$\begin{array}{c}{H}_i=\sum _{j=1}^i\frac{1}{A_j}{Z}_j+\sum _{j=-L}^{-i}\frac{1}{A_{-j}}{Z}_{-j}=\sum _{j=1}^L\frac{1}{A_j}{Z}_j+\frac{1}{A_i}{Z}_i,其中Z_j=B_{j}x(j).\end{array}$$

如果我们将式中的$\frac{1}{A_i}{Z}_i$视为偏置并忽略它，式9可进一步简化，导致所有token共享相同的隐藏状态$H={\sum }_{j=1}^L\frac{1}{A_j}{Z}_j$。在这种情况下，正向和反向扫描的结果可以无缝结合以建立全局上下文，这实际上等效于移除因果掩码并转换为非因果形式。因此，与因果特性相关的第一个挑战得到了解决。尽管上述结果来自双向扫描方法，但显然在这种非因果形式中，不同的扫描路径会产生一致的结果。换句话说，无需设计特定的扫描路径来捕获全局信息。此外，如式9所示，不同token对当前隐藏状态的贡献不再与其空间距离相关。因此，将展平的二维特征图处理为一维序列不再会损害原始的结构关系。这样，第二个挑战也得到了解决。此外，由于整个计算过程可以并行进行，而不必依赖于先前SSMs所需的循环计算方法，训练和推理速度得到了提升。在修改了隐藏状态空间的迭代规则之后，我们按照Mamba2框架，更新了线性形式中相应的张量收缩算法或爱因斯坦求和符号：
$$\begin{array}{c}\begin{array}{rl}Z& =contract(LD,LN\to LND)(X,B)\\ H& =contract(LL,LDN\to ND)(M,Z)\\ Y& =contract(LN,ND\to LD)(C,H)\end{array}\end{array}$$

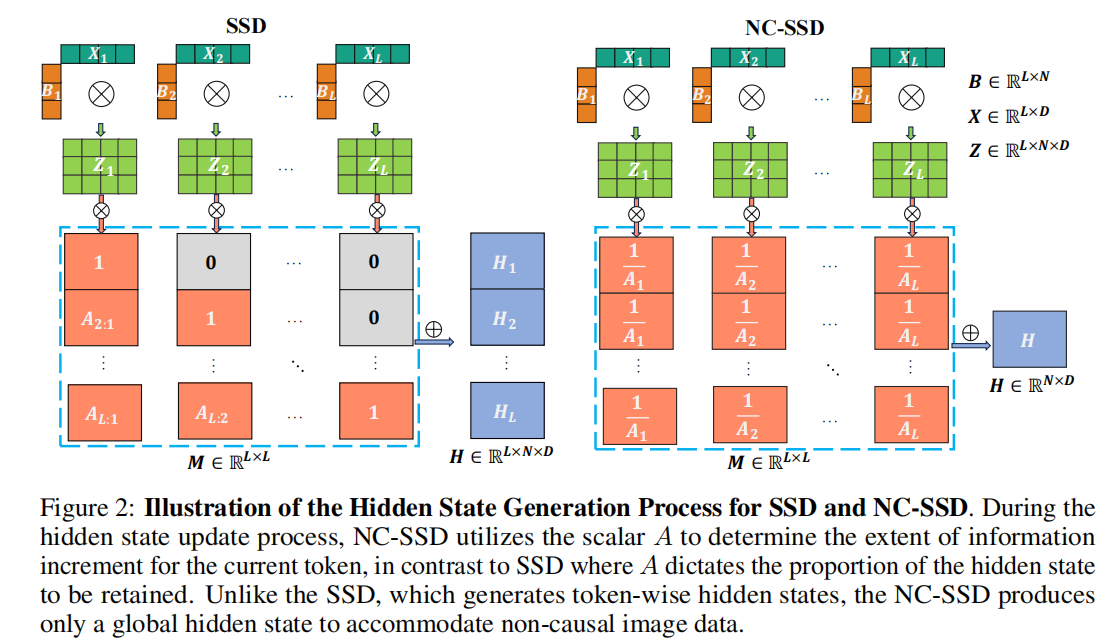
该算法包括三个步骤：第一步使用$B$扩展输入$x$，第二步展开标量SSM递归以创建全局隐藏状态$H$，最后一步将隐藏状态$H$与$C$收缩。为清晰起见，图2展示了SSD和NC-SSD的前两个步骤。与普通SSD相比，虽然第一步的操作保持不变，但在非因果模式下，隐藏状态$H$中的序列长度维度被消除，因为所有token共享相同的隐藏状态。在最后一步中，输出$Y$通过$C$和$H$的矩阵乘法产生。由于$M_{i,j}=\frac{1}{A_j}$，通过消除矩阵$M$的第一维，可将其简化为向量$m\in {\mathbb{R}}^L$。在这种情况下，将$m$与$X$或$B$集成可以进一步将式10的变换简化为：
$$\begin{array}{c}Y=C\left(B^T(X\cdot m)\right)\end{array}$$

这可以被视为线性注意力的一种变体。然而，值得注意的是，正如$A$在Mamba2中起着重要作用一样，向量$m$也至关重要，这在我们的消融研究中得到了证明。在实践中，我们直接使用学习到的$A$而不是$\frac{1}{A}$，因为它们具有相同的值范围。为了更直观地理解式10中$m$的作用，我们将不同头的$m$的平均值可视化，如图3所示。主要来看，$m$关注前景特征，使模型能够优先处理对任务至关重要的元素。

2.3 视觉状态空间对偶性模型

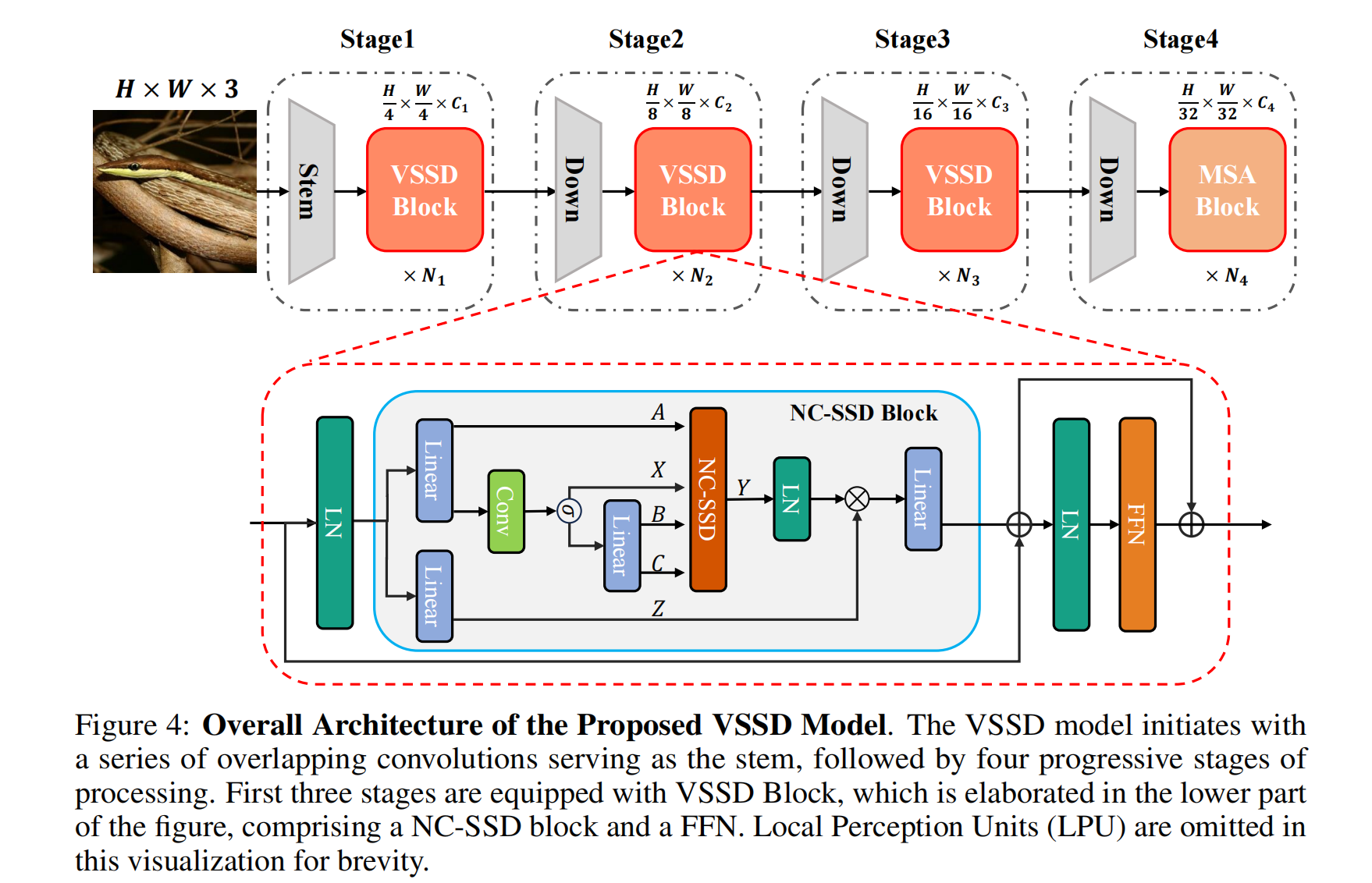
• 块设计：为了增强Mamba2中的SSD块以适应视觉应用，除了仅用NC-SSD替代SSD来开发我们的视觉状态空间对偶性（VSSD）块之外，我们还进行了几项修改。在构建NC-SSD块时，与先前的视觉mamba研究一致，将因果1D卷积替换为 kernel 大小为3的深度卷积（DWConv）。此外，在NC-SSD块之后集成了前馈网络（FFN），以促进跨通道的更好信息交换，并与经典视觉Transformer的既定做法保持一致。此外，在NC-SSD块和FFN之前加入了局部感知单元（LPU），以增强模型的局部特征感知能力。在不同块之间还实现了跳跃连接。VSSD块的架构如图4下部所示。
  

• 与自注意力的混合：Mamba2表明，将SSD与标准多头自注意力（MSA）集成可带来额外的改进。同样，我们的模型也融入了自注意力。然而，与Mamba2在整个网络中均匀分布自注意力不同，我们仅在最后一个阶段用自注意力模块战略性地替换NC-SSD块。这种修改利用了自注意力在处理视觉任务中高级特征方面的强大能力。

• 重叠下采样层：由于分层视觉Transformer和视觉状态空间模型主要采用非重叠卷积进行下采样，最近的研究表明，重叠下采样卷积可以引入有益的归纳偏置。因此，我们在模型中采用了重叠卷积，采用的方式与MLLA相同。为了保持参数数量和计算FLOPs相当，我们相应地调整了模型的深度。

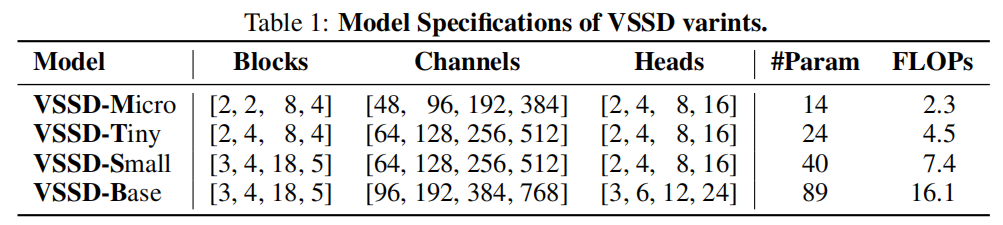
• 整体架构：我们根据上述方法开发了VSSD模型，其架构如图4所示。借鉴先前研究中已建立的视觉骨干网络的设计原则，我们的VSSD模型分为四个分层阶段。前三个阶段采用VSSD块，而最后一个阶段集成了MSA块。VSSD变体的详细架构如表1所示。
  

---

3. 实验结果

3.1 图像分类任务

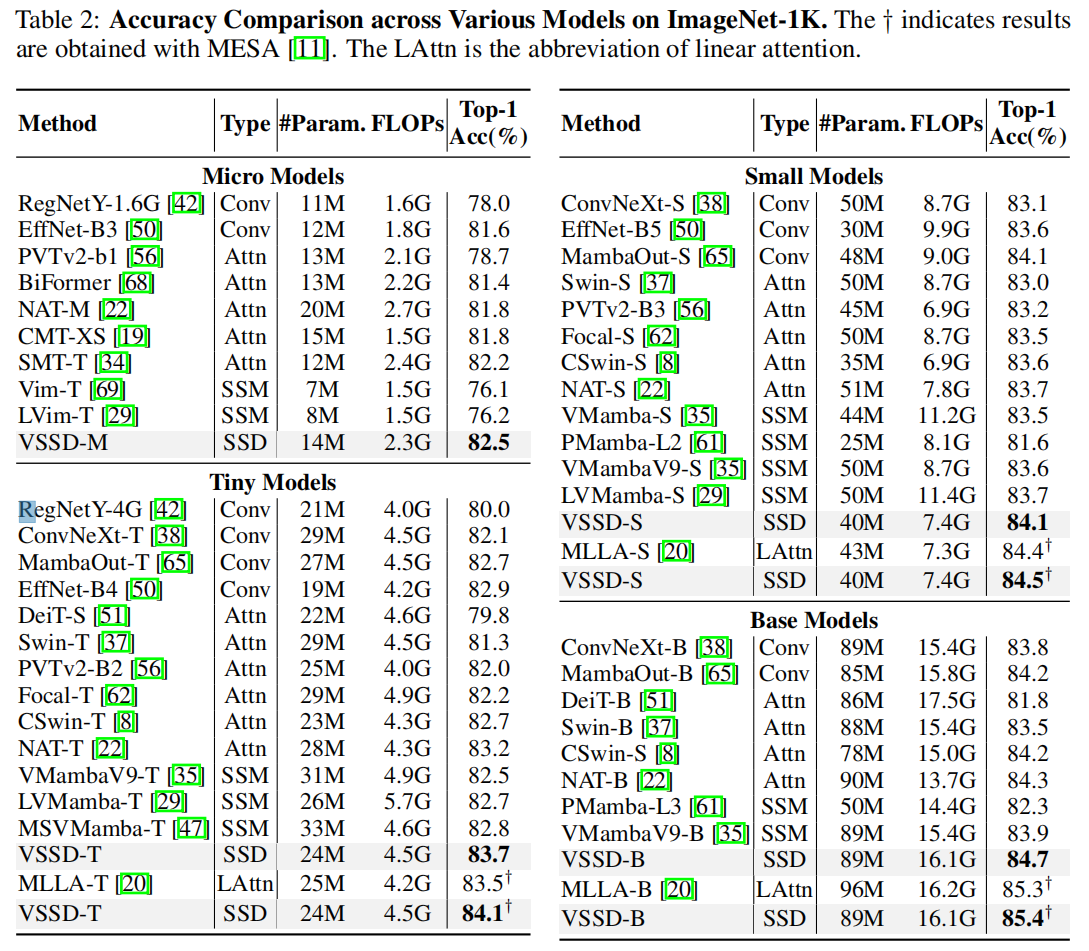
3.2 目标检测任务

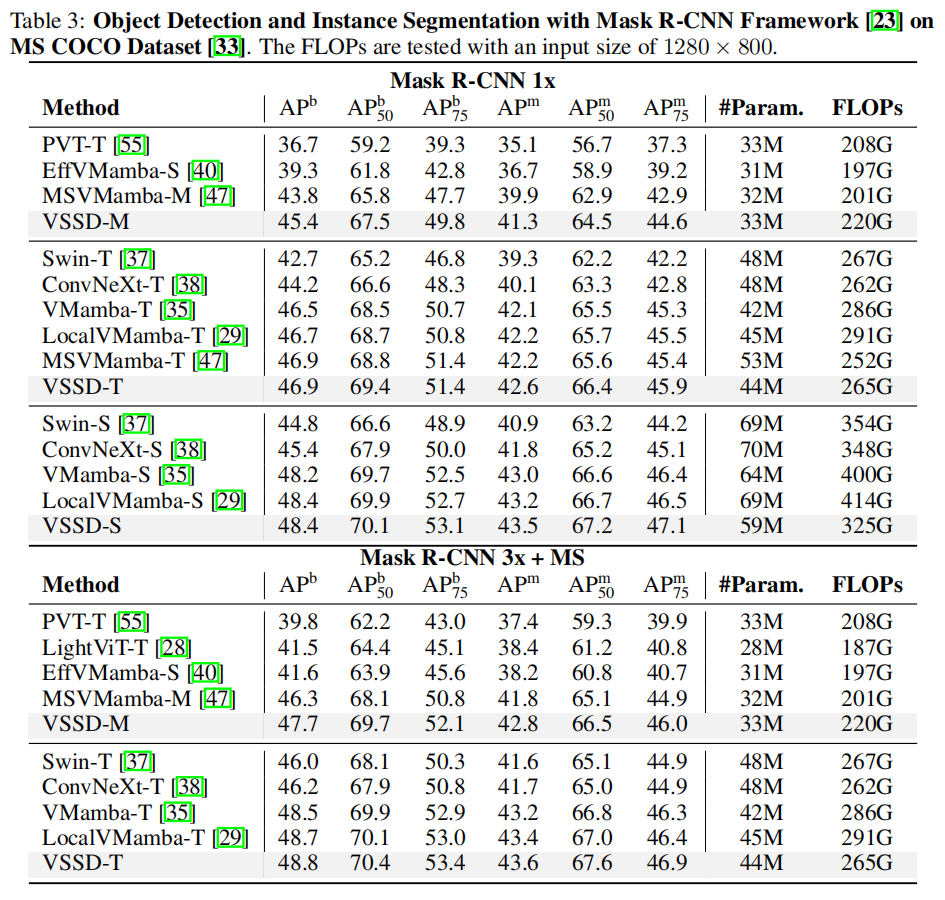
3.3 语义分割任务

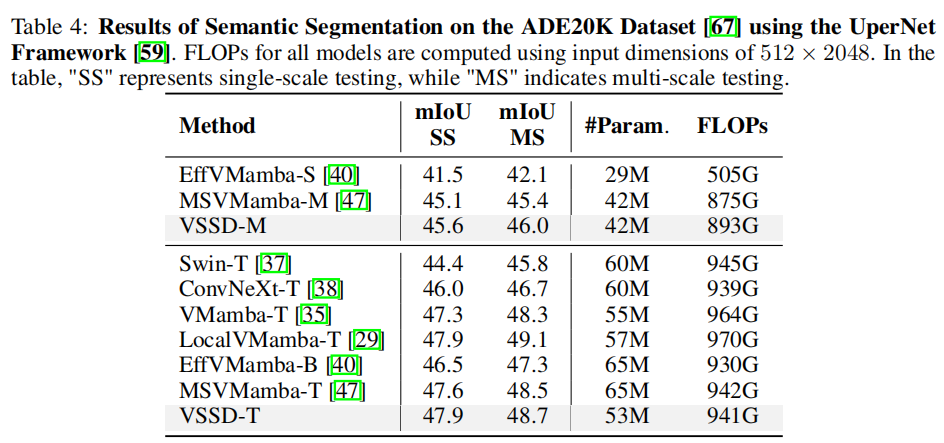
3.4 消融实验

---

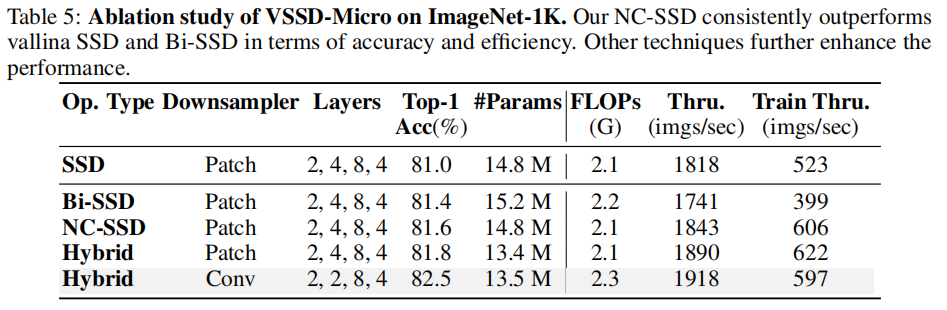
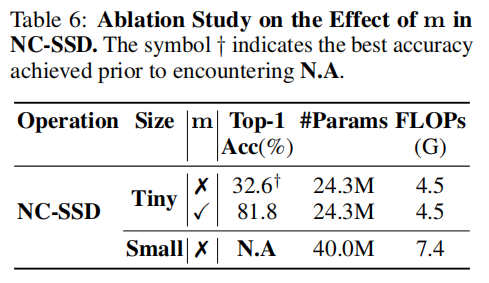
4.局限性与结论

4.1 局限性

• 下游任务性能提升有限：尽管 VSSD 在 ImageNet-1K 图像分类任务中优于其他基于 SSM 的模型，但在下游任务（如目标检测、语义分割）上，与其他 SSM 模型相比，性能提升幅度较小。
• 与顶尖 Transformer 变体存在差距：相较于最先进的视觉 Transformer 变体（如 RMT、Dat++ 等），VSSD 在下游任务上的性能仍有显著差距。
• 缺乏大规模验证：未在更大规模模型或数据集（如 ImageNet-22K）上进行实验，其可扩展性有待进一步探索。

4.2 结论

• NC-SSD 的有效性：通过重新定义状态空间对偶性（SSD）中矩阵 A 的作用并移除因果掩码，提出的非因果 SSD（NC-SSD）成功将 SSD 转换为非因果模式，保留了全局感受野和线性复杂度的优势，同时提升了训练与推理效率
• VSSD 模型的优越性：结合 NC-SSD、混合自注意力机制和重叠下采样等技术，VSSD 在图像分类、目标检测、语义分割等多个基准测试中，与现有 CNN、Transformer 和 SSM-based 模型相比，在相似参数和计算成本下实现了更优或相当的性能。
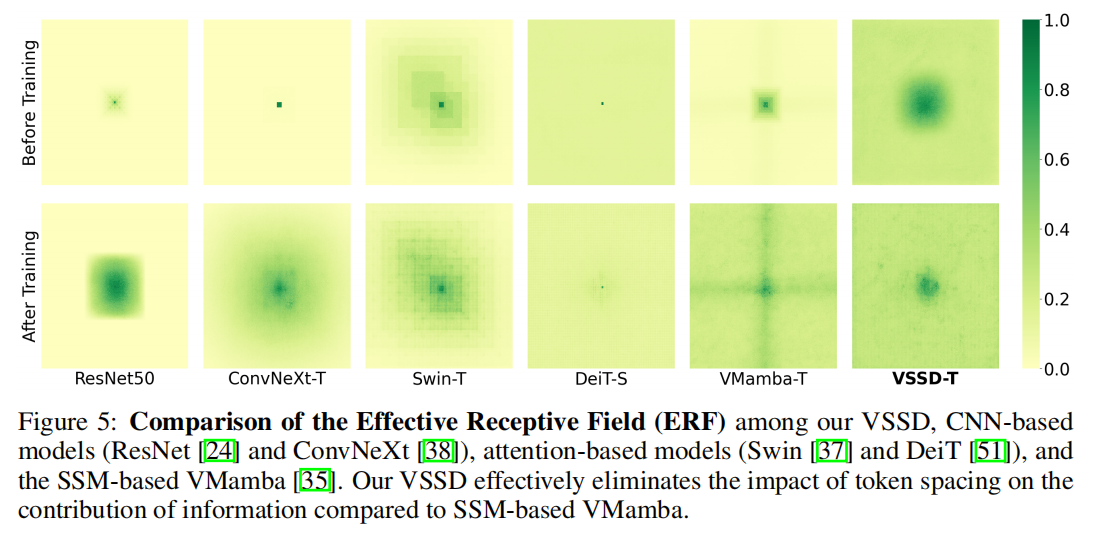
• ERF 优势：如图 5 所示，VSSD 有效消除了 token 间距对信息贡献的影响（相较于 SSM-based 的 VMamba），能更均衡地利用不同位置的信息，更好地保留图像全局结构关系，这是其在视觉任务中表现优异的重要原因。

---