【数据结构】二叉树接口实现指南：递归方法的高效运用 （附经典算法OJ）

文章目录

1、前置说明

1、定义二叉树结点结构

2、创建新节点

3、手动创建二叉树

2、二叉树的遍历

1、前序，中序和后序遍历

1.1、二叉树前序遍历

1.2、二叉树中序遍历

1.3、二叉树后序遍历

2、二叉树层序遍历

 3、二叉树的基础操作

1、二叉树节点总数

2、叶子节点个数

3、二叉树高度

4、二叉树第k层节点数

5、查找目标节点

6、通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树

7、销毁

4、经典算法OJ

1、单值二叉树

2、检查两颗树是否相同

3、另一棵树的子树

1、前置说明

前面的文章我们根据完全二叉树的结构特点，用顺序存储的方式实现了堆相关的接口以及堆排序。下面我们用链式结构来实现普通二叉树的基本操作，但在实现之前，我们需要先创建一棵二叉树，然后才能学习相关的操作，由于我们对二叉树的结构掌握还不够深入，我们就先手动地创建一棵二叉树，等我们对二叉树的结构有了进一步的理解，再反过来实现二叉树真正的创建。

二叉树是： 1、空树

2、非空：根结点，根结点的左子树、根结点的右子树组成的。

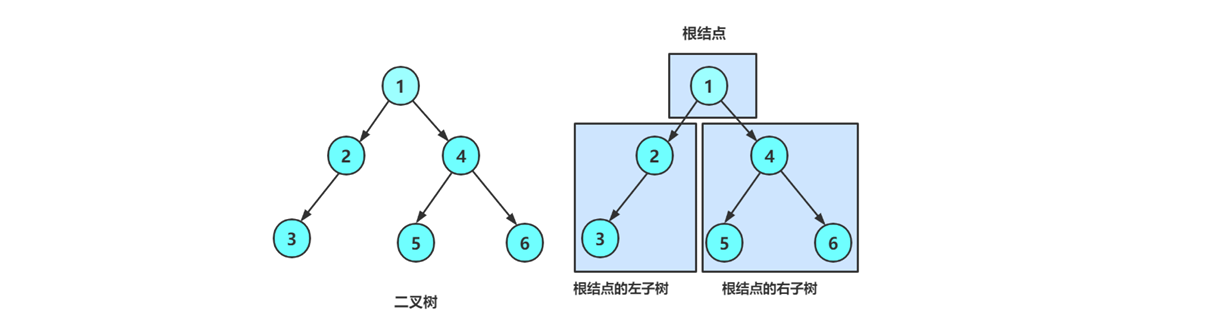
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。 

1、定义二叉树结点结构

用链式结构实现二叉树，节点结构就类似于链表的节点。同时，我们还需要两个结构体类型的指针来连接孩子节点。

//定义二叉树存储的数据类型
typedef int BTDateType;
//定义节点结构
typedef struct BinaryTree
{BTDateType val;struct BinaryTree* left;struct BinaryTree* right;
}BTNode;

2、创建新节点

BTNode* BuyBTNode(BTDateType x)
{BTNode* pst = (BTNode*)malloc(sizeof(BTNode));if (pst == NULL){perror("malloc");exit(1);}pst->val = x;pst->left = NULL;pst->right = NULL;
}

3、手动创建二叉树

BTNode* BinaryTreeCreat()
{//创建二叉树的节点BTNode* s1 = BuyBTNode(1);BTNode* s2 = BuyBTNode(2);BTNode* s3 = BuyBTNode(3);BTNode* s4 = BuyBTNode(4);BTNode* s5 = BuyBTNode(5);BTNode* s6 = BuyBTNode(6);//连接节点成为二叉树s1->left = s2;s2->left = s3;s2->right = s7;s1->right = s4;s4->left = s5;s4->right = s6;return s1;
}

2、二叉树的遍历

1、前序，中序和后序遍历

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的结点进行相应的操作，并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

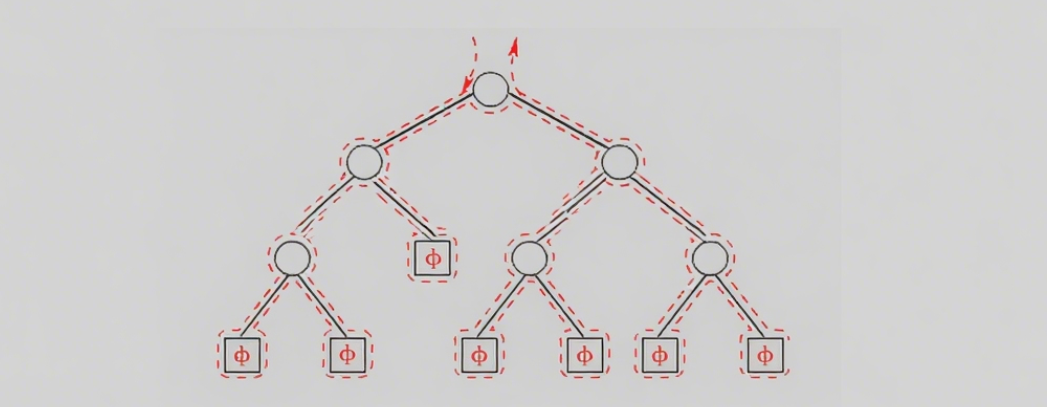
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(先序遍历)——访问根结点的操作发生在遍历其左右子树之前，根->左子树->右子树。

2. 中序遍历——访问根结点的操作发生在遍历其左右子树之中（间），左子树->根->右子树。

3. 后序遍历——访问根结点的操作发生在遍历其左右子树之后，左子树->右子树->根。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。 

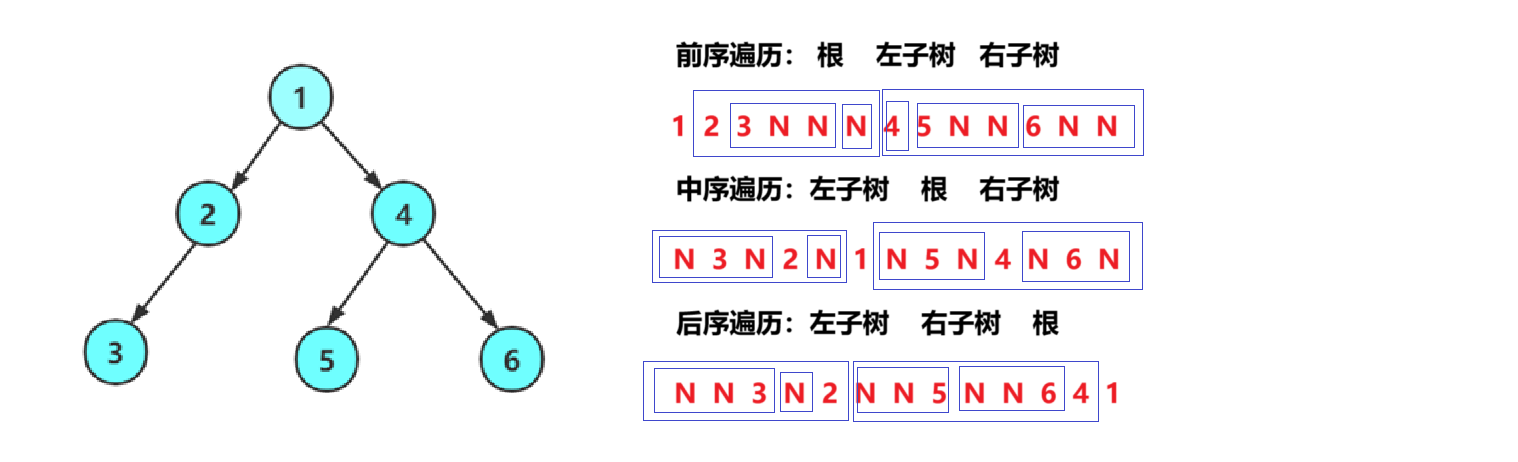
// 二叉树前序遍历 
void prevOrder(BTNode* root);
// 二叉树中序遍历
void midOrder(BTNode* root);
// 二叉树后序遍历
void afterOrder(BTNode* root);

1.1、二叉树前序遍历

前序遍历递归图解：

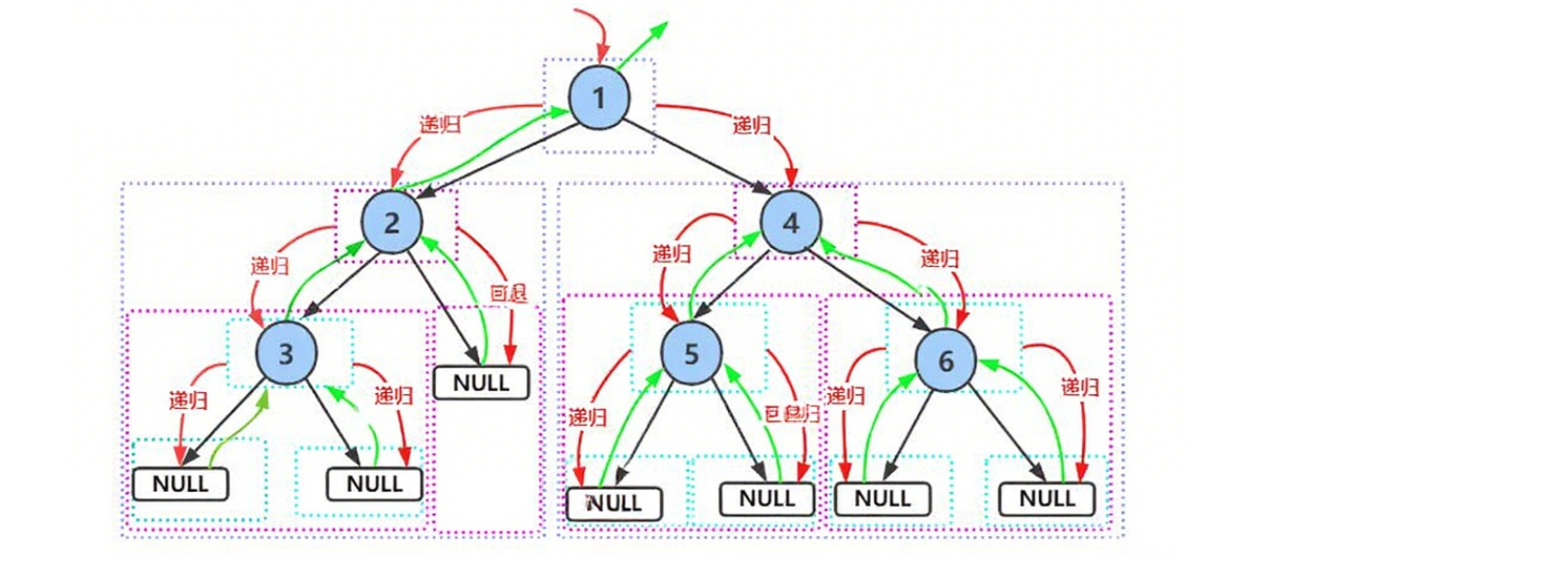
//前序遍历：根  左子树  右子树
void prevOrder(BTNode* root)
{//打印空节点if (root == NULL){printf("N ");return;}//打印根节点的值printf("%d ", root->val);//递归遍历左子树prevOrder(root->left);//递归遍历右子树prevOrder(root->right);
}

输出结果：

1 2 3 N N N 4 5 N N 6 N N

为了能够更加直观的理解递归调用的过程，我们画图来感受一下，后面用递归实现接口的过程中，我们也可以用类似的方法来画图，帮助我们理解！！！

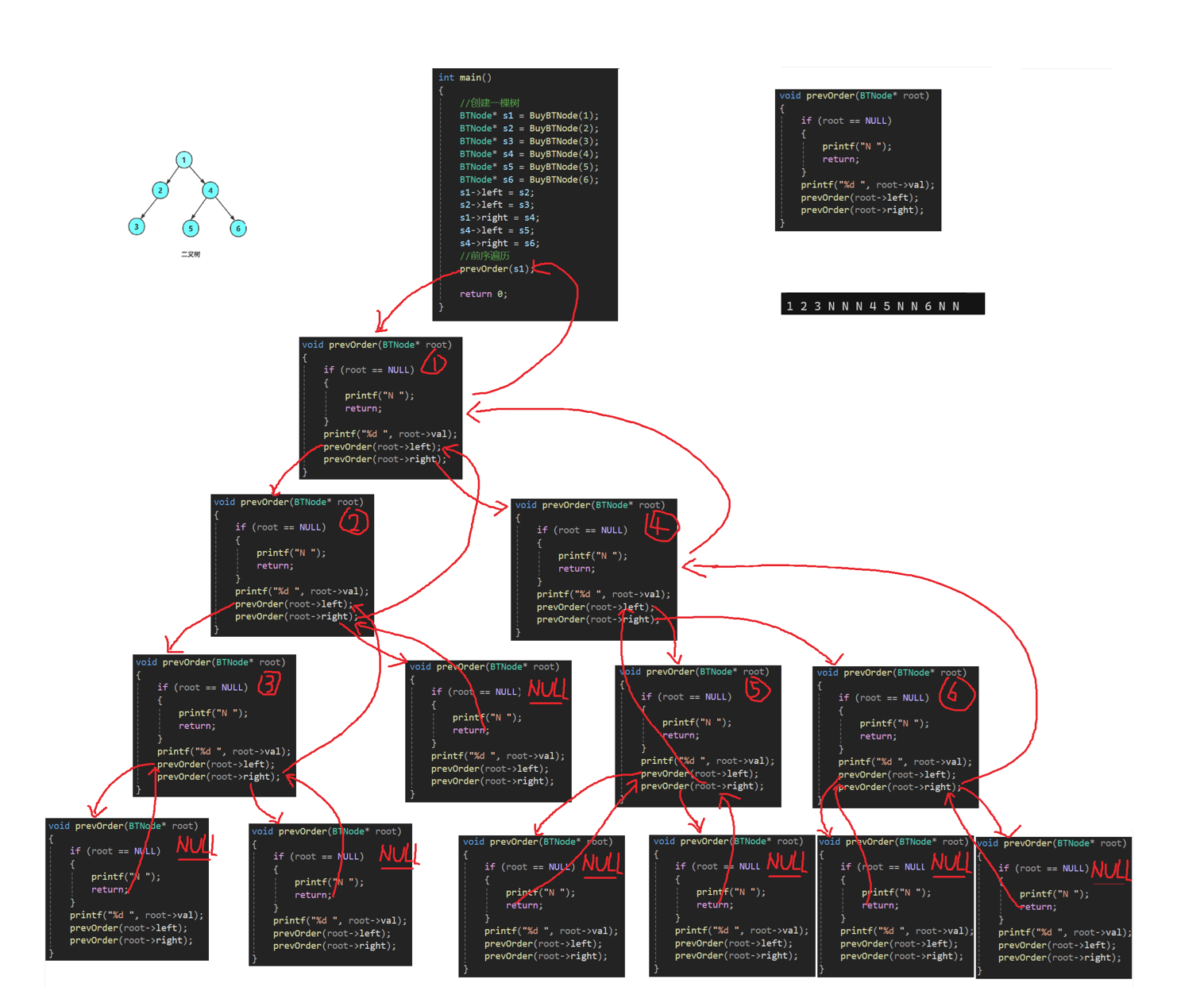
1.2、二叉树中序遍历

//中序遍历：左子树  根  右子树
void midOreder(BTNode* root)
{   //打印空节点if (root == NULL){printf("N ");return;}//递归遍历左子树midOreder(root->left);//打印根节点的值printf("%d ", root->val);//递归遍历右子树midOreder(root->right);
}

输出结果

N 3 N 2 N 1 N 5 N 4 N 6 N

1.3、二叉树后序遍历

//后序遍历：左子树  右子树  根
void afterOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}//递归遍历左子树afterOrder(root->left);//递归遍历右子树afterOrder(root->right);//打印根节点的值printf("%d ", root->val);
}

输出结果

N N 3 N 2 N N 5 N N 6 4 1

2、二叉树层序遍历

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根结点所在 层数为1，层序遍历就是从所在二叉树的根结点出发，首先访问第一层的树根结点，然后从左到右访问第2层 上的结点，接着是第三层的结点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

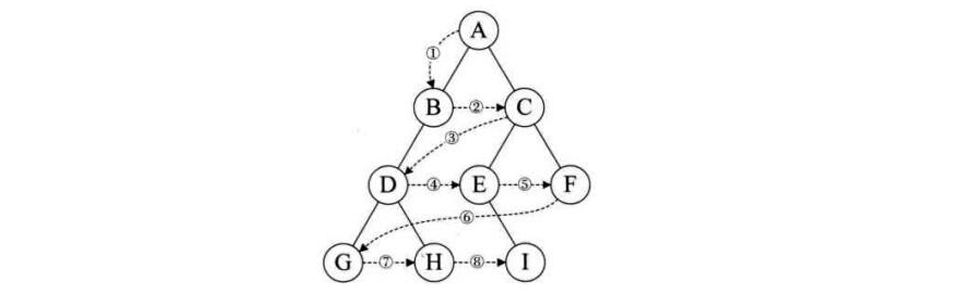
 3、二叉树的基础操作

1、二叉树节点总数

思路1：遍历二叉树，创建一个变量来记录节点个数，但是，每次函数调用都是在栈区开辟空间，数据在函数调用结束后就会销毁，所以要创建全局变量，或者用static修饰的全局变量（但是在调用之前需要初始化为0）。当遇到某个节点的左孩子或者右孩子为空时，递归结束，开始返回。

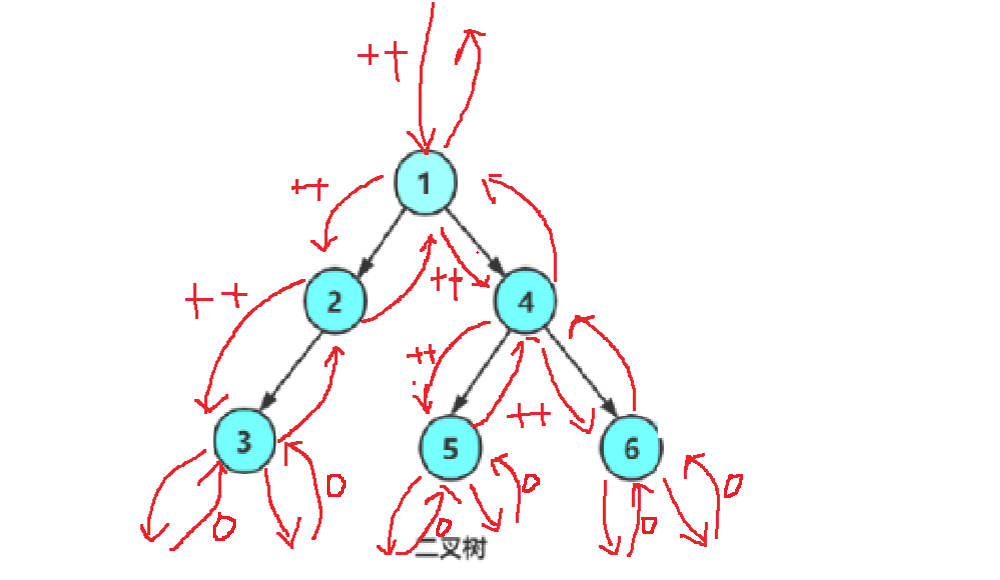
int size = 0;//全局变量
//static int size = 0;int TreeSize(BTNode* root)
{//递归结束，遇到空树，返回if (root == NULL)return 0;else++size;//遍历二叉树TreeSize(root->left);TreeSize(root->right);return size;
}

还有一种简单的写法，用三目操作符来判断，但是不容易理解

int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

递归调用图解： 

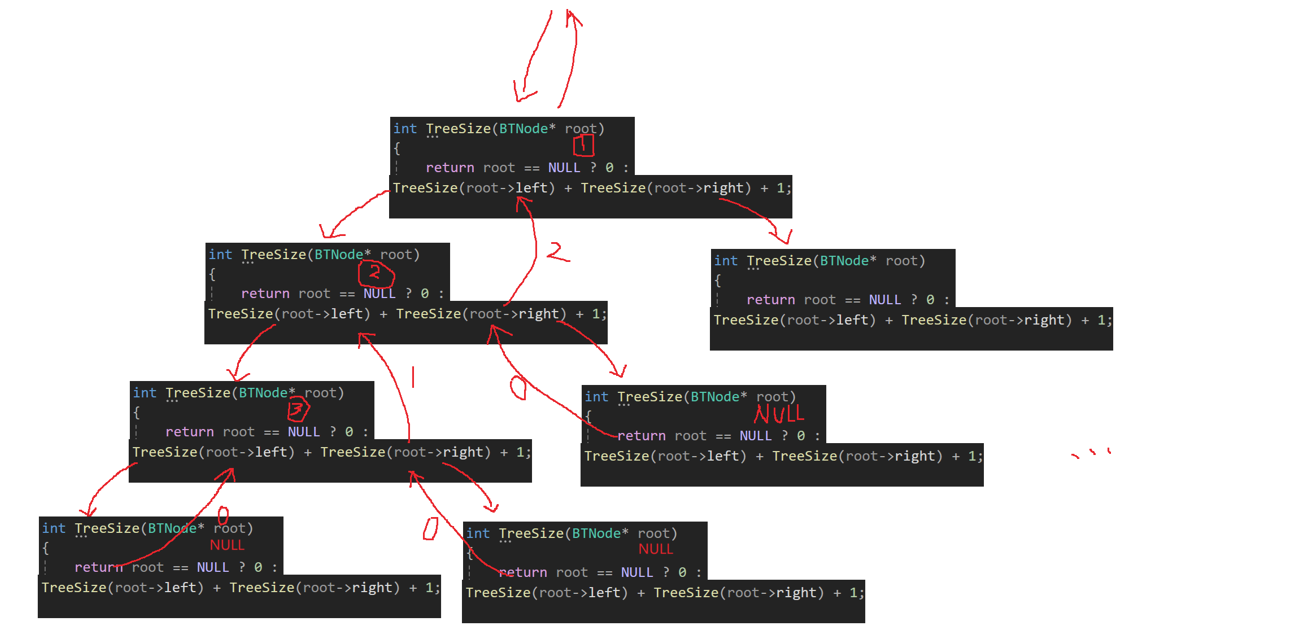
 思路2：将size作为实参，但是为了让形参改变的同时改变实参的值，我们需要传实参的地址。

//将size作为参数
void TreeSize(BTNode* root, int* psize)
{if (root == NULL)return 0;else++(*psize);TreeSize(root->left, psize);TreeSize(root->right, psize);
}

2、叶子节点个数

思路：遍历二叉树，将二叉树不断分为左子树与右子树，找左孩子与右孩子都不存在的节点，即叶子节点，然后将所有左子树与右子树的叶子节点加起来。

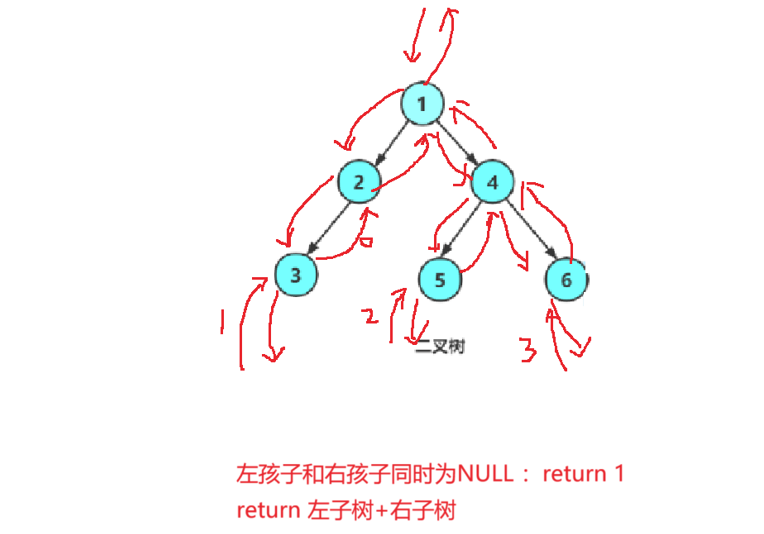
//计算叶子节点个数
int TreeLeafCount(BTNode* root)
{//遇到空节点，递归结束条件if (root == NULL){return 0;}//当左子树与右子树同时为空时为叶子节点if ((root->left == NULL) && (root->right == NULL)){return 1;}//叶子节点数等于左子树+右子树return TreeLeafCount(root->left) + TreeLeafCount(root->right);
}

3、二叉树高度

思路：递归遍历二叉树的左子树与右子树的同时，记下左子树与右子树的高度，然后比较左子树与右子树，二叉树的高度就是较高的一个加上根节点的高度。

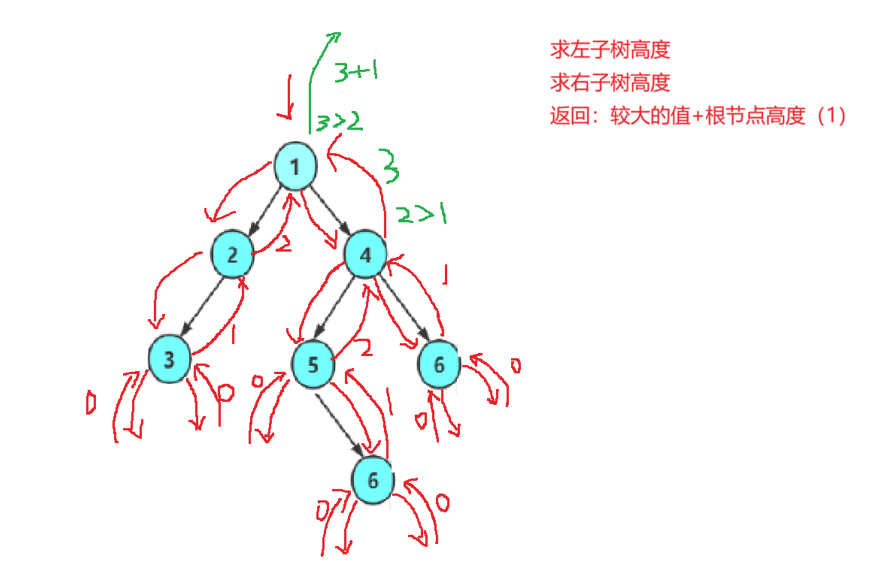
//计算二叉树高度
int TreeHeight(BTNode* root)
{//递归结束条件if (root == NULL){return 0;}//记下返回值，防止造成时间效率低下//左子树高度int leftheight = TreeHeight(root->left);//右子树高度int rightheight = TreeHeight(root->right);//高度为较大的高度+根节点的高度if (leftheight > rightheight)return leftheight + 1;elsereturn rightheight + 1;//三目操作符//return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

4、二叉树第k层节点数

思路：计算二叉树第k层节点数，递归遍历二叉树的左子树与右子树，计算第k-1层的节点的不为空的左孩子和右孩子的个数，返回左子树与右子树k-1层的节点的不为空的左孩子和右孩子的个数的和。

//计算第k层有多少个节点
int TreeNodecount_k(BTNode* root, int k)
{//递归结束条件if (root == NULL)return 0;//处理特殊情况if (k == 1)return 1;//注意不能使用k--或者--k,这样递归一次,后一次调用相当于k-1-1return TreeNodecount_k(root->left, k - 1) + TreeNodecount_k(root->right, k - 1);
}

5、查找目标节点

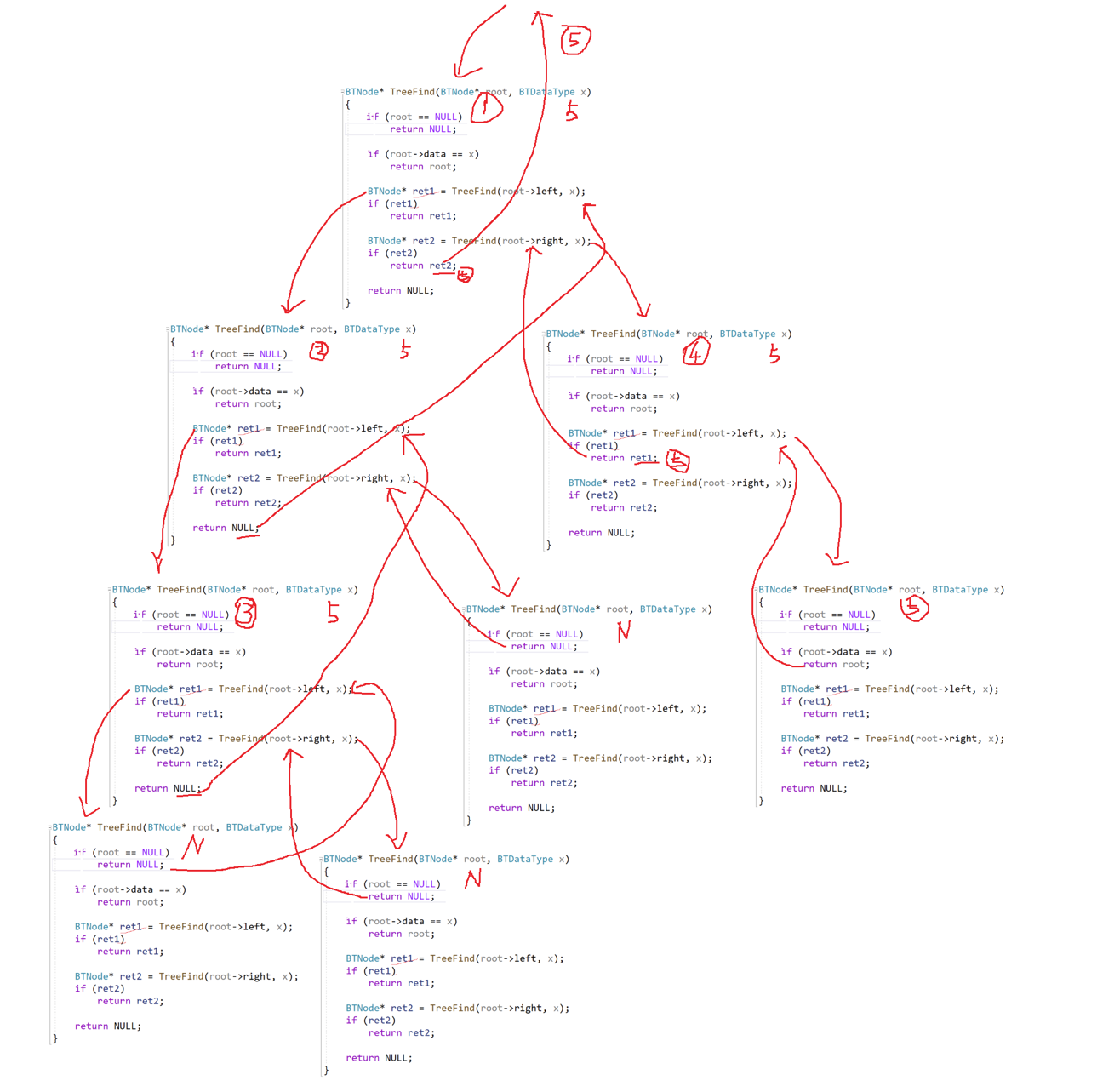
递归遍历左子树与右子树

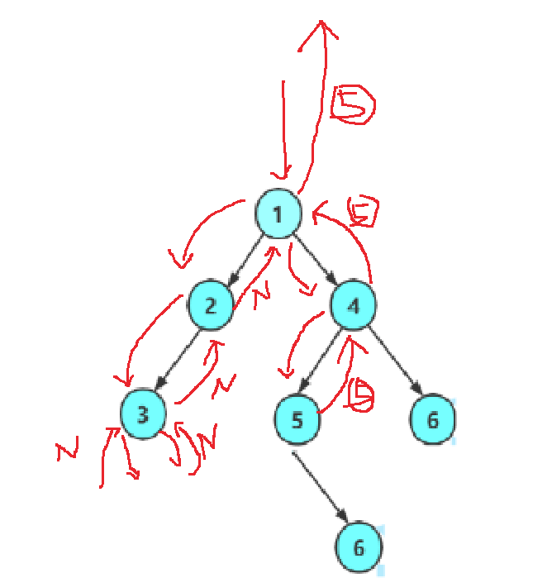
//查找目标节点
BTNode* TreeFind(BTNode* root, BTDateType x)
{if (root == NULL)return NULL;if (root->val == x){return root;}//记下返回值BTNode* ret1 = TreeFind(root->left, x);//找到了，就返回if (ret1)return ret1;BTNode* ret2 = TreeFind(root->right, x);if (ret2)return ret2;return NULL;
}

6、通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树

//定义二叉树存储的数据类型
typedef char BTDateType;

 ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。

//创建一颗二叉树
BTNode* CreatTree(char* a, int* pi)
{//递归结束条件，同时处理空树if (a[*pi] == '#'){(*pi)++;return NULL;}//不是'#'就为节点开辟空间BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->val = a[(*pi)++];//递归遍历数组newnode->left = CreatTree(a, pi);newnode->right = CreatTree(a, pi);return newnode;
}int main()
{char arr[] = { "ABD##E#H##CF##G##" };int i = 0;BTNode* root = CreatTree(arr, &i);return 0;
}

7、销毁

思路：递归遍历二叉树，用后序遍历，防止将根释放而找不到左子树与右子树。

//销毁二叉树
//后序遍历：左子树->右子树->根，防止将根释放而找不到左子树与右子树
void TreeDestry(BTNode* root)
{if (root == NULL){return;}//递归遍历左子树TreeDestry(root->left);//递归遍历右子树TreeDestry(root->right);free(root);
}

4、完整源码 

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<math.h>
#include"Queue.h"//定义二叉树的节点
typedef int BTDateType;
typedef struct BinaryTree
{BTDateType val;struct BinaryTree* left;struct BinaryTree* right;
}BTNode;BTNode* BuyBTNode(BTDateType x)
{BTNode* pst = (BTNode*)malloc(sizeof(BTNode));if (pst == NULL){perror("malloc");exit(1);}pst->val = x;pst->left = NULL;pst->right = NULL;
}
BTNode* BinaryTreeCreat()
{//创建一棵树BTNode* s1 = BuyBTNode(1);BTNode* s2 = BuyBTNode(2);BTNode* s3 = BuyBTNode(3);BTNode* s4 = BuyBTNode(4);BTNode* s5 = BuyBTNode(5);BTNode* s6 = BuyBTNode(6);BTNode* s7 = BuyBTNode(7);s1->left = s2;s2->left = s3;s2->right = s7;s1->right = s4;s4->left = s5;s4->right = s6;//s5->right = s7;return s1;
}
//前序遍历：根  左子树  右子树
void prevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);prevOrder(root->left);prevOrder(root->right);
}//中序遍历：左子树  根  右子树
void midOreder(BTNode* root)
{if (root == NULL){printf("N ");return;}midOreder(root->left);printf("%d ", root->val);midOreder(root->right);
}
//后序遍历：左子树  右子树  根
void afterOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}afterOrder(root->left);afterOrder(root->right);printf("%d ", root->val);
}//计算节点总数
//每次函数调用都是在栈区开辟空间，数据在函数调用结束后就会销毁，所以要创建全局变量，或者用static修饰的全局变量（但是在调用之前需要初始化为0）//错误示范：static修饰的变量在函数作用域内，又static修饰的变量不会销毁，所以在main函数中反复调用会导致结果不断增加
//int TreeNodeCount(BTNode* root)
//{
//	static int size = 0;
//	if (root == NULL)
//	{
//		return 0;
//	}
//	size++;
//	TreeNodeCount(root->left);
//	TreeNodeCount(root->right);
//	return size;
//}int size = 0;//全局变量
//static int size = 0;int TreeSize(BTNode* root)
{if (root == NULL)return 0;else++size;TreeSize(root->left);TreeSize(root->right);return size;
}////将size作为参数
//void TreeSize(BTNode* root, int* psize)
//{
//	if (root == NULL)
//		return 0;
//	else
//		++(*psize);
//
//	TreeSize(root->left, psize);
//	TreeSize(root->right, psize);
//}//int TreeSize(BTNode* root)
//{
//	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
//}//计算叶子节点个数
int TreeLeafCount(BTNode* root)
{if (root == NULL){return 0;}if ((root->left == NULL) && (root->right == NULL)){return 1;}return TreeLeafCount(root->left) + TreeLeafCount(root->right);
}//计算二叉树高度
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}//记下返回值，防止造成时间效率低下int leftheight = TreeHeight(root->left);int rightheight = TreeHeight(root->right);//高度为较大的高度+根节点的高度if (leftheight > rightheight)return leftheight + 1;elsereturn rightheight + 1;//三目操作符//return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}////使用fmax()函数求较大的值
//int TreeHeight(BTNode* root)
//{
//	if (root == NULL)
//		return 0;
//
//	return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
//}//计算第k层有多少个节点
int TreeNodecount_k(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;//注意不能使用k--或者--k,这样递归一次,后一次调用相当于k-1-1return TreeNodecount_k(root->left, k - 1) + TreeNodecount_k(root->right, k - 1);
}//查找目标节点
BTNode* TreeFind(BTNode* root, BTDateType x)
{if (root == NULL)return NULL;if (root->val == x){return root;}//记下返回值BTNode* ret1 = TreeFind(root->left, x);//找到了，就返回if (ret1)return ret1;BTNode* ret2 = TreeFind(root->right, x);if (ret2)return ret2;return NULL;
}//销毁二叉树
//后序遍历：左子树->右子树->根，防止将根释放而找不到左子树与右子树
void TreeDestry(BTNode* root)
{if (root == NULL){return;}TreeDestry(root->left);TreeDestry(root->right);free(root);
}//测试
int main()
{BTNode* root = BinaryTreeCreat();//前序遍历prevOrder(root);printf("\n");//中序遍历midOreder(root);printf("\n");//后序遍历afterOrder(root);printf("\n");//计算二叉树节点总个数//size = 0;//printf("TreeSize:%d\n", TreeSize(root));//size = 0;//printf("TreeSize:%d\n", TreeSize(root));//size = 0;//printf("TreeSize:%d\n", TreeSize(root));//int size = 0;//TreeSize(root, &size);//printf("TreeSize:%d\n", size);//size = 0;//TreeSize(root, &size);//printf("TreeSize:%d\n", size);//printf("%d ", TreeSize(root));//printf("%d ", TreeSize(root));//求叶子节点的个数//printf("%d\n", TreeLeafCount(root));////求二叉树的高度//printf("%d\n", TreeHeight(root));////求二叉树第k层有多少个节点//printf("%d\n",TreeNodecount_k(root, 3));////查找目标节点//BTNode* ret = TreeFind(root, 5);//printf("%d\n", ret->val);return 0;
}

5、经典算法OJ

1、单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

题目描述：

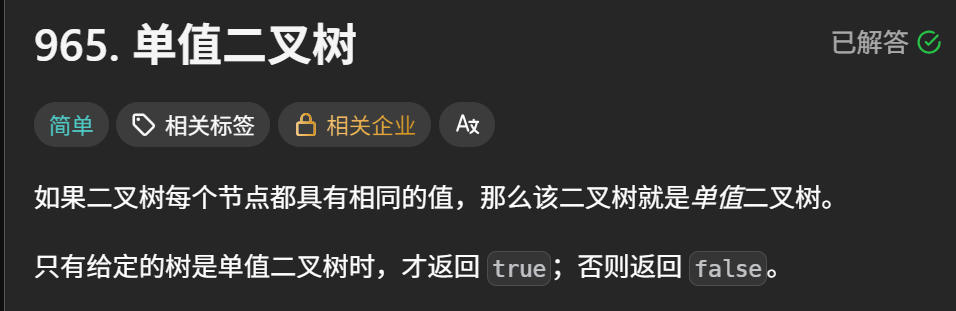
示例： 

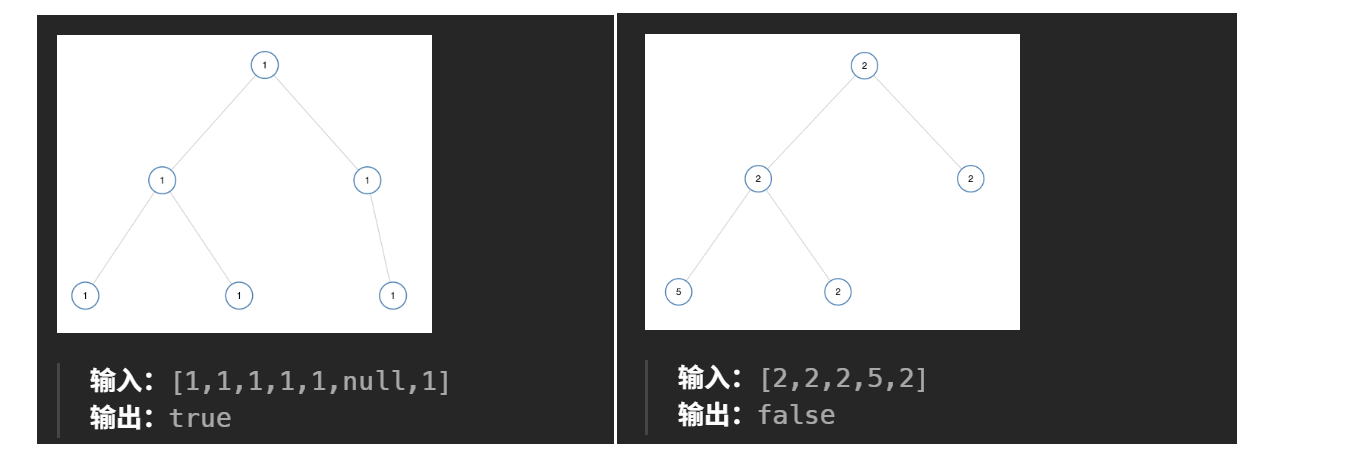
bool _isUnivalTree(struct TreeNode* root,int x) 
{  //处理空树情况，同时为递归结束条件if(root==NULL){return true;}//排除空树，且只要不等于根结点的值，就返回falseif(root->left&&root->left->val!=x){return false;}if(root->right&&root->right->val!=x){return false;}//递归遍历左子树与右子树return _isUnivalTree(root->left, x)&&_isUnivalTree(root->right,x);
}bool isUnivalTree(struct TreeNode* root) 
{return _isUnivalTree(root,root->val);
}

2、检查两颗树是否相同

100. 相同的树 - 力扣（LeetCode）

题目描述：

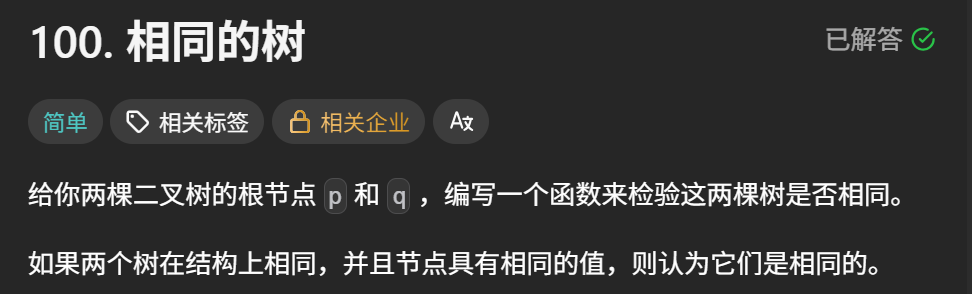
示例： 

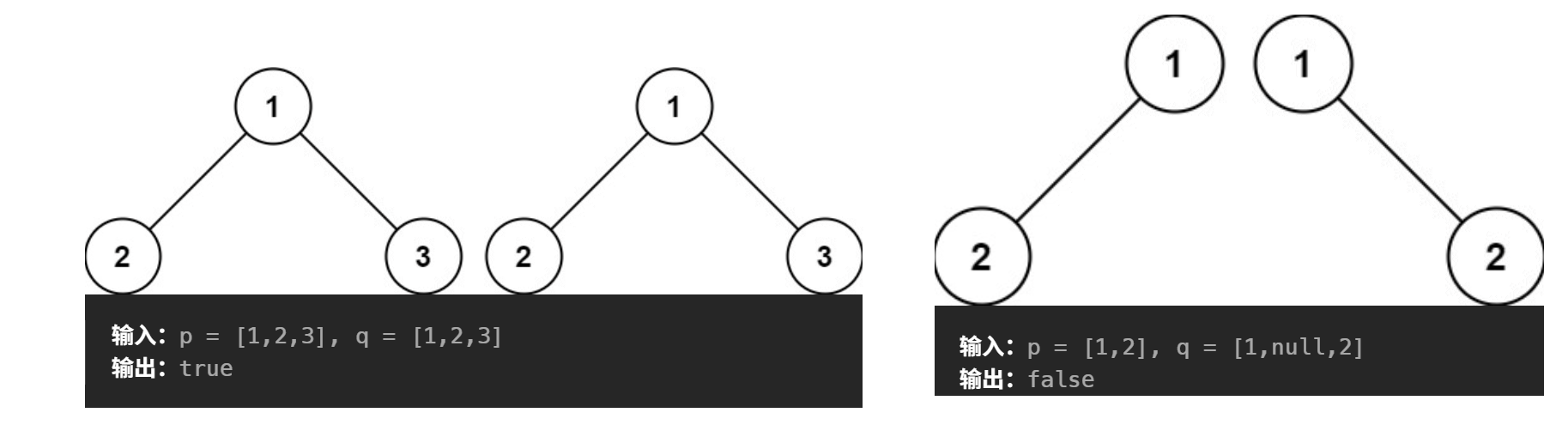
 首先判断如果都是空树时返回真；一个为空一个不为空时返回false；值不相等，返回false。然后递归遍历左子树和右子树，左子树与左子树比较，右子树与右子树比较，当递归到都是空时返回true（与刚开始的判空对应），递归到一个为空一个不为空时返回false（与刚开始的判断一个为空一个不为空对应），最后左子树与左子树相等且右子树与右子树相等则返回true；反之，返回false。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{//都是空树或递归到都是空时返回真if(p==NULL&&q==NULL){return true;}//一个为空一个不为空或递归到一个为空一个不为空时返回falseif(p==NULL||q==NULL){return false;}//值不相等，返回falseif(p->val!=q->val){return false;}//递归遍历左子树和右子树，左子树与左子树比较，右子树与右子树比较return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

3、另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

题目描述：

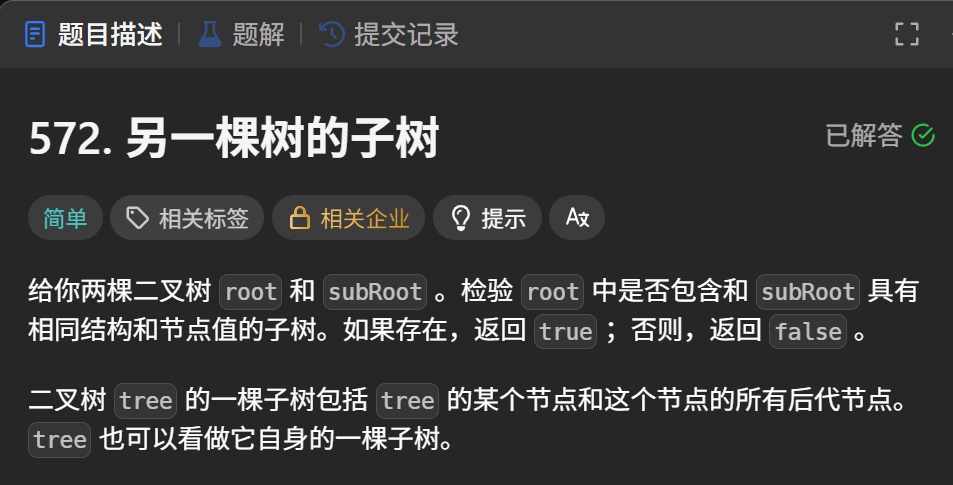
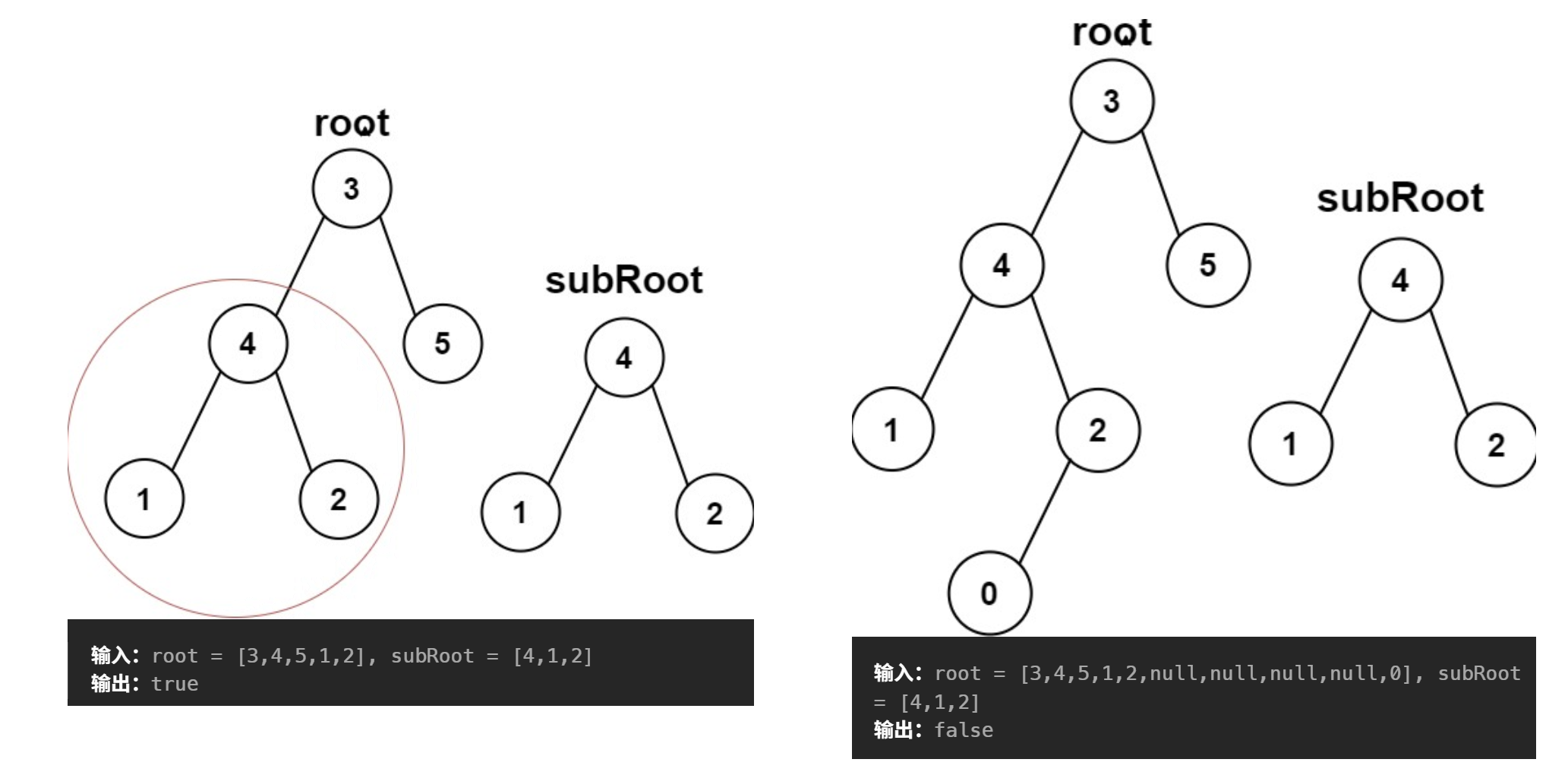 不断递归遍历一棵树的左子树和右子树，然后判断这棵树的左子树与右子树与另一棵树是否相等。可以借助前面实现的判断两棵树是否相等的函数。 

bool isSameTree(struct TreeNode*p,struct TreeNode*q)
{//都为空if(p==NULL&&q==NULL){return true;}//一个为空，一个不为空if(p==NULL||q==NULL){return false;}if(p->val!=q->val){return false;}return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) 
{if(root==NULL){return false;}if((root->val==subRoot->val) && (isSameTree(root,subRoot))){ return true;}//将root拆分为左子树和右子树与subRoot比较return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/bicheng/91974.shtml
繁体地址，请注明出处：http://hk.pswp.cn/bicheng/91974.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

自动驾驶控制算法——LQR控制算法

自动驾驶控制算法——LQR控制算法

自动驾驶控制算法——LQR控制算法 文章目录自动驾驶控制算法——LQR控制算法**一、LQR 是什么&#xff1f;**二、LQR 原理2.1 线性状态空间模型 (State–Space Model)2.2 二次型性能指标 JJJ2.3 代数黎卡提方程 (ARE)2.4 特点总结2.5 一句话总结 LQR 原理&#xff1a;2.5.1 场景…
阅读更多...
Jotai：React轻量级原子化状态管理，告别重渲染困扰

Jotai：React轻量级原子化状态管理，告别重渲染困扰

简介 Jotai 是一个为 React 提供的原子化状态管理库&#xff0c;采用自下而上的方法来进行状态管理。Jotai 受 Recoil 启发&#xff0c;通过组合原子来构建状态&#xff0c;并且渲染基于原子依赖性进行优化。这解决了 React 上下文的额外重新渲染问题&#xff0c;并消除了对 m…
阅读更多...
C语言数据结构（7）贪吃蛇项目2.贪吃蛇项目实现

C语言数据结构（7）贪吃蛇项目2.贪吃蛇项目实现

8. 核心逻辑实现分析 8.1 游戏主逻辑 程序开始就设置程序支持本地模式&#xff0c;然后进入程序的主逻辑。 主逻辑分为3个过程&#xff1a; • 游戏开始&#xff08;GameStart&#xff09;完成游戏的初始化。 • 游戏运行&#xff08;GameRun&#xff09;完成游戏运行逻辑的…
阅读更多...
知识蒸馏 - 最小化KL散度与最小化交叉熵是完全等价的

知识蒸馏 - 最小化KL散度与最小化交叉熵是完全等价的

知识蒸馏 - 最小化KL散度与最小化交叉熵是完全等价的 flyfish KL散度与交叉熵的数学关系 对于两个概率分布 PPP&#xff08;真实分布&#xff09;和 QQQ&#xff08;模型预测分布&#xff09;&#xff0c;KL散度的定义是&#xff1a; DKL(P∥Q)∑xP(x)log⁡(P(x)Q(x)) D_{KL}(P…
阅读更多...
设计心得——网络包的处理

设计心得——网络包的处理

一、介绍 在程序的开发中&#xff0c;网络开发是一个重要的应用场景。毕竟这些年IT行业之所以火&#xff0c;主要还是互联网&#xff08;移动互联网&#xff09;带来的。网络开发&#xff0c;有各种平台、框架以及系统和库提供的API&#xff0c;如果说网络开发是一个特别复杂和…
阅读更多...
sqli-labs通关笔记-第30关GET字符注入(WAF绕过 双引号闭合 手工注入+脚本注入两种方法)

sqli-labs通关笔记-第30关GET字符注入(WAF绕过 双引号闭合 手工注入+脚本注入两种方法)

目录 一、源码分析 1、index.php代码审计 2、login.php代码审计 3、java_implimentation函数 4、whitelist函数 5、SQL安全性分析 二、渗透实战 1、进入靶场 2、WAF探测 &#xff08;1&#xff09;触发WAF &#xff08;2&#xff09;绕过WAF 3、手工注入 &#xf…
阅读更多...
【openlayers框架学习】九：openlayers中的交互类（select和draw）

【openlayers框架学习】九：openlayers中的交互类（select和draw）

文章目录openlayers进阶28 openlayers中的事件29 openlayers中select交互类的使用30 openlayers中select常见的配置选项31 openlayers中绘制交互类&#xff08;Draw&#xff09;openlayers进阶 28 openlayers中的事件 常用进行事件交互的对象&#xff1a;map\view\source29 o…
阅读更多...
Java企业级应用性能优化实战

Java企业级应用性能优化实战

在企业级Java应用开发中，性能优化是确保系统稳定运行的关键因素。本文将从多个维度深入分析Java应用性能瓶颈，并提供实战优化方案。 🎯 性能优化核心领域 1. 对象操作性能优化 在企业应用中，对象拷贝是一个高频操作，特别是在分层架构中的DO、DTO、VO转换。选择合适的拷…
阅读更多...
LLM Prompt与开源模型资源(3)如何写一个好的 Prompt

LLM Prompt与开源模型资源(3)如何写一个好的 Prompt

学习材料&#xff1a;https://www.hiascend.com/developer/courses/detail/1935520434893606913 &#xff08;3.5&#xff09;学习时长&#xff1a; 预计 60 分钟学习目的&#xff1a; 了解提示工程的定义与作用熟悉提示工程的关键技术相关概念掌握基于昇腾适配的大模型提示工程…
阅读更多...
日志管理工具 ——ELK Stack

日志管理工具 ——ELK Stack

一、ELK Stack 概述1.1 核心组件ELK Stack&#xff08;现更名为 Elastic Stack&#xff09;是一套开源的日志收集、存储、分析和可视化平台&#xff0c;由三个核心组件构成&#xff1a;Elasticsearch&#xff1a;分布式搜索引擎&#xff0c;负责日志数据的存储、索引和快速查询…
阅读更多...
SpringAI：AI工程应用框架新选择

SpringAI：AI工程应用框架新选择

Spring AI 是一个用于 AI 工程的应用框架 Spring AI 是一个用于 AI 工程的应用框架。其目标是将可移植性和模块化设计等 Spring 生态系统设计原则应用于 AI 领域，并推广使用 POJO 作为应用程序的构建块到 AI 领域。 Spring AI 的核心是解决 AI 集成的基本挑战：将企业数据和…
阅读更多...
Kettle 开源ETL数据迁移工具从入门到实战

Kettle 开源ETL数据迁移工具从入门到实战

ETL&#xff08;Extract, Transform, Load&#xff09;工具是用于数据抽取、转换和加载的软件工具&#xff0c;用于支持数据仓库和数据集成过程。Kettle作为传统的ETL工具是纯 java 开发的开源的 ETL工具&#xff0c;用于数据库间的数据迁移 。可以在 Linux、windows、unix 中运…
阅读更多...
Maven中的bom和父依赖

Maven中的bom和父依赖

maven最全避坑指南写完后&#xff0c;发现自己对于bom和父pom的理解还是不够深入&#xff0c;特此转载DeepSeek的回答&#xff0c;和大家一起学习了。 在 Maven 的依赖管理中&#xff0c;父 POM (Parent POM) 和 BOM (Bill of Materials) 都是用于实现集中化管理和控制的核心机…
阅读更多...
Python 操作 Word 文档：主流库对比与选择指南

Python 操作 Word 文档：主流库对比与选择指南

在办公自动化、报告生成、数据处理等领域&#xff0c;利用 Python 程序化地创建、读取或修改 Microsoft Word 文档 (.docx 格式) 是一项非常实用的技能。Python 生态中有多个优秀的库可以完成这项任务&#xff0c;但它们各有侧重和优缺点。选择哪一个“最好用”&#xff0c;关键…
阅读更多...
怎么修改论文格式呢？提供一份论文格式模板

怎么修改论文格式呢？提供一份论文格式模板

注！！！本文内容是作者自己整理的一份模板，仅供参考，各位如何修改，还需要看学校的要求。 一、参考文献 1、有一定数量的近几年参考文献、不宜过多中文文献 英文期刊模板 [1] Taesoo K, Sooyoung K, Kyunghan L, et al. Special issue on 6G and satellite communication…
阅读更多...
MVC 发布

MVC 发布

MVC 发布 引言 MVC（Model-View-Controller）模式是一种广泛应用于软件开发的架构模式。它将应用程序分为三个主要部分：模型（Model）、视图（View）和控制器（Controller）。这种模式不仅提高了代码的可维护性和可扩展性，而且使得开发者可以更加专注于各个组件的开发。本文…
阅读更多...
arkui 动画曲线

arkui 动画曲线

参考文档 https://developer.huawei.com/consumer/cn/doc/harmonyos-references/js-apis-curve#curvesinterpolatingspring10 可视化工具网站 https://easingwizard.com/ https://www.desmos.com/calculator/k01p40v0ct?langzh-CN 基本介绍 import { curves } from kit.A…
阅读更多...
大语言模型（LLM）技术架构与工程实践：从原理到部署

大语言模型（LLM）技术架构与工程实践：从原理到部署

在自然语言处理领域，大语言模型（LLM）已成为颠覆性技术。从 GPT 系列到 LLaMA、ChatGLM，这些参数规模动辄百亿甚至万亿的模型，不仅实现了流畅的自然语言交互，更在代码生成、逻辑推理等复杂任务中展现出惊人能力。本文将从技术底层拆解 LLM 的核心架构，分析训练与推理的关…
阅读更多...
python后端之DRF框架（上篇）

python后端之DRF框架（上篇）

一、DRF框架介绍 1、web应用开发模式 1.1、前后端不分离1.2、前后端分离2、RESTful介绍 RESTful是目前最流行的API设计风格 &#xff0c; REST 指的是一组架构约束条件和原则。满足这些约束条件和原则的应用程序或设计就是 RESTful。 1、每一个URI代表1种资源&#xff1b; 2、客…
阅读更多...
信创数据库-DM（达梦）数据库安装教程

信创数据库-DM（达梦）数据库安装教程

官方安装文档在这&#xff1a;安装前准备 | 达梦技术文档 本文也是基于这个来写的&#xff0c;微调了一下。 1&#xff0c;下载安装包 体验版直接到官方下载即可&#xff1a;产品下载 | 达梦在线服务平台 如果是有需要商业版等&#xff0c;需要联系客服申请。 安装包要选择CPU…
阅读更多...
最新文章

Copyright @ 2022~2023