一、简介

IOU的全称为交并比（Intersection over Union），是目标检测中使用的一个概念，IoU计算的是“预测的边框”和“真实的边框”的交叠率，即它们的交集和并集的比值。最理想情况是完全重叠，即比值为1。

二、计算

《一文搞懂IoU发展历程》GIoU、DIoU、CIoU、EIoU、αIoU、SIoU-阿里云开发者社区

目标检测-Iou(交并比)理解-CSDN博客

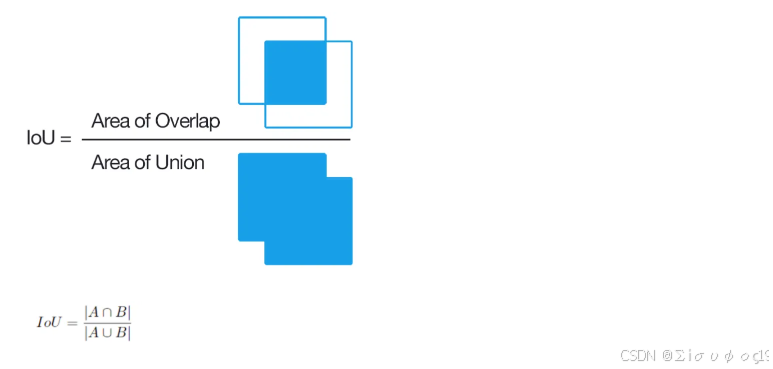
IoU等于“预测的边框”和“真实的边框”之间交集和并集的比值。IoU计算如下图，B1为真实边框，B2为预测边框 

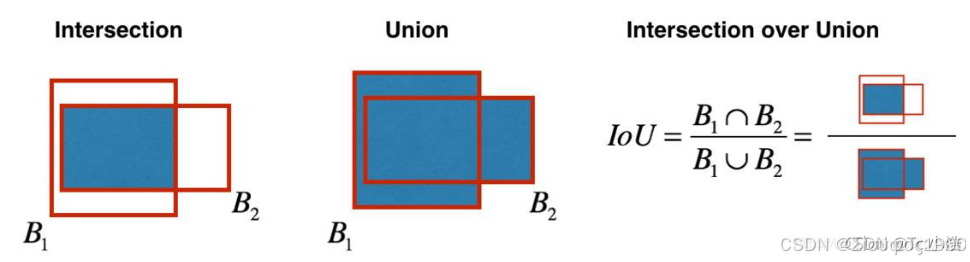
计算如下：

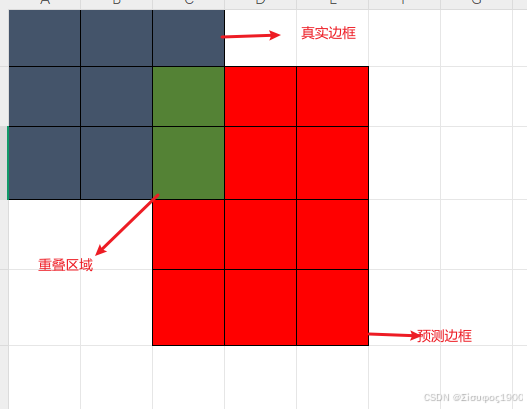
union=9+12=21

inter=2

IOU=2/21=0.095

 

import numpy as np
def Iou(box1, box2, wh=False):if wh == False:xmin1, ymin1, xmax1, ymax1 = box1xmin2, ymin2, xmax2, ymax2 = box2else:xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)# 获取矩形框交集对应的左上角和右下角的坐标（intersection）xx1 = np.max([xmin1, xmin2])yy1 = np.max([ymin1, ymin2])xx2 = np.min([xmax1, xmax2])yy2 = np.min([ymax1, ymax2])	# 计算两个矩形框面积area1 = (xmax1-xmin1) * (ymax1-ymin1) area2 = (xmax2-xmin2) * (ymax2-ymin2)inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#计算交集面积iou = inter_area / (area1+area2-inter_area+1e-6) 　#计算交并比return iou