强化学习-CH9 策略梯度方法

当策略被表示为函数时，通过优化目标函数可以得到最优策略。 这种方法称为策略梯度。策略梯度方法是基于策略的，而之前介绍的方法都是基于值的。其本质区别在于基于策略的方法是直接优化关于策略参数的目标函数。

9.1 策略表示：从表格到函数

表格形式：

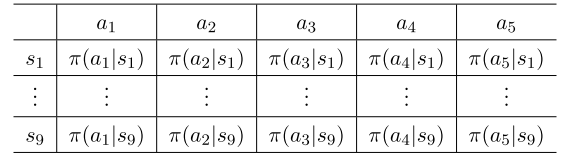
函数形式：

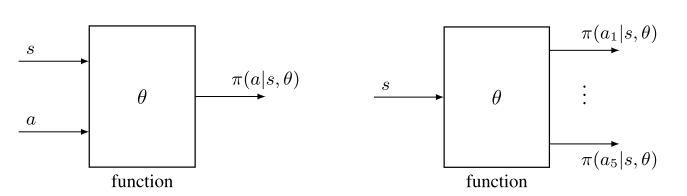
区别：

（1）定义最优策略：当用表格表示时，如果策略可以最大化每个状态值，即其状态值大于或等于其他任意策略的状态值，则将其定义为最优策略。 当用函数表示时，如果策略可以最大化一个标量目标函数，则将其定义为最优策略。

（2）更新政策：当用表格表示时，可以通过直接更改表中的条目来更新策略。 当用参数化函数表示策略时，不能再以这种方式更新策略。 相反，它只能通过改变参数θ来更新。

（3）检索一个动作的概率： 在表格的情况下，可以通过查找表中的相应条目直接获得动作的概率。 在函数表示的情况下，需要在函数中输入（s, a）来计算其概率。

9.2 目标函数：定义最优策略

目标函数1：平均状态值

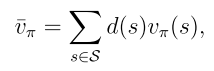
d(s)是状态s的权重，也可以理解为状态s的概率分布，因此可以重写为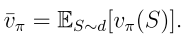

如何选择d(s):

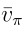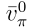（1）第一种也是最简单的情况是d与策略π无关。 在这种情况下，将d表示为d0，并将表示为，以表明分布与策略无关。

（2）第二种情况是d依赖于策略π。 在这种情况下，通常选择d为dπ，它是π下的平稳分布。

等价表达式：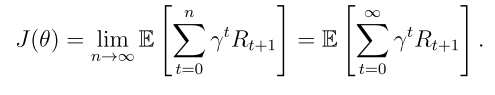

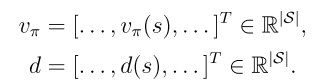
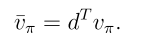
目标函数2：平均奖励

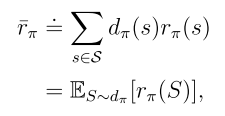
其中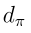是平稳分布，且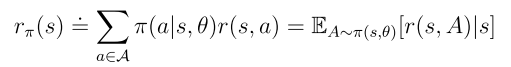是从状态s出发的即时奖励的期望值。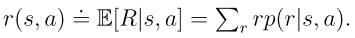

等价表达式：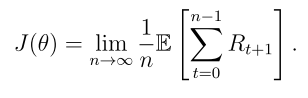

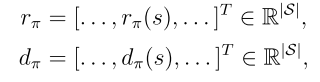
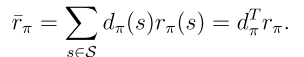
所有这些目标函数都是π的函数。 因为π是由θ参数化的，所以这些函数是θ的函数。 换句话说，不同的θ值可以产生不同的目标函数值。因此，可以寻找θ的最优值来最大化这些函数值。 这是策略梯度方法的基本思想。

9.3 目标函数的梯度

定理9.1（策略梯度定理）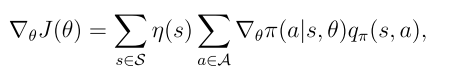

等价形式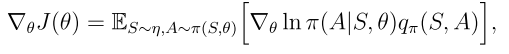

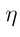是状态的概率分布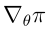，是π关于θ的梯度

9.4 蒙特卡罗策略梯度

用梯度上升算法来最大化目标函数以获得最佳策略

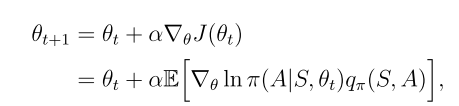
用随机梯度替换真实梯度

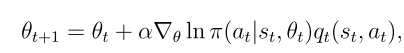
20150037)]

用随机梯度替换真实梯度

[外链图片转存中…(img-Sa4XqvJh-1757420150037)]