目录
🔍 若用递归计算每一项,会发生什么?
Horner's Rule(霍纳法则)
第一步:我们从最原始的泰勒公式出发
第二步:从形式上重新观察展开式
🌟 第三步:引出霍纳法则(Horner’s Rule)
第四步:如何用这个结构重写泰勒展开式?
完整代码
从迭代转换成递归逻辑
“迭代”和“循环”
当前递归方法的结构回顾:
double num = 1, den = 1;double taylor(int n, double x) {if (n == 0) return 1;double res = taylor(n - 1, x); // 一次函数调用num *= x; // 分子:一次乘法den *= n; // 分母:一次乘法return res + num / den;
}
这一版已经做了初步优化:我们通过 累计 num 和 den 来避免重复调用 pow(x,n) 和 factorial(n)。
但这只是相对优化,我们现在要分析:
🔍 若用递归计算每一项,会发生什么?
我们从第 0 项到第 n 项共计算 n+1项,每一项的乘法成本如下:
| 第 k 项 | 乘法次数 |
|---|---|
| k = 0 | 0 |
| k = 1 | 1 |
| k = 2 | 2 |
| ... | ... |
| k = n | n |
所以总乘法次数为:

✅ 因此,乘法总次数为 O(n^2)!
🚨 问题在哪里?
-
你对每一项都重新计算幂和阶乘
-
导致重复计算,浪费大量 CPU 时间
-
如果你希望
n = 50、n = 100,程序变慢得很明显
🤔 有没有更好的方式?
是的。你就引出了今天的主角:
Horner's Rule(霍纳法则)
我们可以尝试换一种展开方式,让我们不必每次都分别去计算幂和阶乘。
我们将展开式进行重写:

也就是一种嵌套式计算结构。
这个就是 Horner 法则的思路 —— 逐层乘进去、逐层加出来,避免重复乘法和幂展开。

第一步:我们从最原始的泰勒公式出发
以 e^x 为例,泰勒展开是:

这表达得很清晰,每一项结构都类似:
-
分子是 x^k
-
分母是 k!
所以直觉上,我们就写了:
double num = 1; // 分子
double den = 1; // 分母double taylor(int n, double x) {if (n == 0) return 1; // 1️⃣ 锚点:停止递归double res = taylor(n - 1, x); // 2️⃣ 先构造前面所有项的和num *= x; // 3️⃣ 然后再更新状态den *= n;return res + num / den; // 4️⃣ 当前项加进去
}递归方法的思路解析,可以看我之前发表的文章:
数据结构:递归:泰勒展开式(Taylor Series Expansion)-CSDN博客
但是整个算法需要 O(n^2) 次的乘法。
于是我们问自己:
❓有没有一种办法,我们不显式地计算幂和阶乘,而是用一种更聪明的方式重写它?
第二步:从形式上重新观察展开式
我们把:

我们尝试反向收敛:
从最后一项往前看。
设:

假设我们已知最后一项是:

我们问:有没有可能构造出一个结构:

我们知道这种结构是逐层“乘进去再加”,是一种“嵌套结构”。
这时候,你会自然联想到:
🌟 第三步:引出霍纳法则(Horner’s Rule)
Horner's Rule 是一种重写多项式的方式,使其变成嵌套乘加结构,从而节省乘法次数。
给你一个多项式:
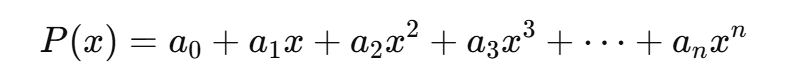
它可以等价重写成:

第一步:从最后一项开始反向思考
先写出最后一项:

但我们不这么直接展开,而是尝试合并每一项,构建嵌套结构。我们回顾一下:
第二步:尝试因式提取,构造嵌套结构
我们从最后一项往回包,先只保留最后一项:

向前一项加:
 再加:
再加:

最后加 1 项:

第三步:得出结论(形式)
最终你得到的就是:

这就是 Horner 法则在泰勒展开中的精确结构!

第四步:如何用这个结构重写泰勒展开式?
霍纳法则告诉我们:
如果你有一个嵌套表达式,它从最深处开始乘加,就可以从最后一项反向累积计算。
我们的目标是以某种结构计算它,让乘法次数最少。
观察这个嵌套结构你会发现:
-
每一层都包含一个 “1 + x / k * (之前的结果)”
-
最里面的是
1 -
然后不断被
x/k包裹
它是一个“逐层包裹”的结构,每一层是:

这说明我们可以从“最深的那一层”开始往外展开。
于是你意识到这就是一种“右折叠(right fold)”,即:
result = 1;
result = 1 + x * result / 4;
result = 1 + x * result / 3;
result = 1 + x * result / 2;
result = 1 + x * result / 1;
从后往前包,每次乘进去一个 x / i,再加 1。
所谓「右折叠」就是我们从表达式的最右边开始构建,逐层包起来。
1 + x/4 ← 第 1 层(最里面)
1 + x/3 * (1 + x/4) ← 第 2 层
1 + x/2 * (...) ← 第 3 层
1 + x/1 * (...) ← 第 4 层
你看到一种非常明显的重复:
每次的操作是:
result = 1 + x * result / i;
从哪个 i 开始?
-
最深一层是对应最大项 n
-
然后是 n - 1
-
最后是 i = 1
所以你会写一个反向的循环:
for (int i = n; i > 0; --i)
初始值设置为:
double result = 1.0; // 最里层的恒定值
为什么是 1.0?
因为你可以认为最内层就是 1 + 0,也就是我们从最后一项 x^n / n! 折叠得到的值是最深的那个 1,逐层向外构建。
完整代码
double horner_taylor(int n, double x) {double result = 1.0; // 最深嵌套项for (; n > 0; n--) { // 从内往外迭代result = 1 + x * result / n; // 每次构造一层}return result;
}
从迭代转换成递归逻辑
递归的本质是:
用一个函数在每一层调用自己,把循环变成函数调用链。
从上面的迭代式:

你可以直接转换成递归表达式:
double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result; // 最深嵌套项(base case)result = 1 + x / n * result; return horner_recursive(n - 1, x);
}

| 循环版结构 | 递归版结构 |
|---|---|
| 从 n 逐步降到 1 | 从 n 递归到 0(递归终止条件) |
每次更新 result = ... | 每次返回 1 + x * 下层 / n |
初始 result = 1.0 | horner_recursive(0, x) = 1.0 |
两者实际上是完全等价的计算结构。
“迭代”和“循环”
什么是“循环”(loop)?
-
循环是语法结构
-
是编程语言提供的控制流语句(
for、while、do-while) -
它的作用是:重复执行某段代码
比如:
for (int i = 0; i < 10; ++i) {// 执行 10 次
}
什么是“迭代”(iteration)?
-
迭代是算法行为
-
意思是:基于前一个结果,不断构造下一个结果
-
它不依赖一定要用循环语法,也可以用递归实现!
举例说明:
✅ 迭代行为 + 循环实现
double result = 1;
for (int i = n; i > 0; --i)result = 1 + x * result / i;
-
每一轮基于上一轮的
result -
所以这是一个迭代算法
-
同时用了
for,所以也是一个循环结构
✅ 迭代行为 + 递归实现
double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result; // 最深嵌套项(base case)result = 1 + x / n * result; return horner_recursive(n - 1, x);
}
-
每一层基于“下一层”的结果
-
所以也是一种迭代算法
-
但这次用的是递归结构
🚫 循环 ≠ 迭代(反例)
for (int i = 0; i < 10; ++i) {cout << "Hello\n";
}
-
这使用了循环,但没有迭代行为(没有前后状态依赖)
-
所以它是循环,但不是迭代

)

)






的记录)

)


——STUDIO传输的MCP服务端)


-实例与实现解释)
