---

1.摘要

传统DBO存在探索与开发能力失衡、求解精度低以及易陷入局部最优等问题。因此，本文提出了带有缩减因子分数阶蜣螂优化算法（FORDBO），其通过缩减因子实现探索与开发能力的动态平衡。分数阶微积分策略用于调整搜索区域边界，使算法能更有效地聚焦于潜在的优质解空间。此外，重复更新机制进一步增强了跳出局部最优的能力。

2.蜣螂优化算法DBO原理

【智能算法】蜣螂优化算法（DBO）原理及实现

3.改进策略

缩减因子

DBO在探索与开发能力的平衡上存在不足，容易出现全局探索不充分或局部开发不精确的问题，参数的随机选取也会导致优化过程不稳定。为解决这些问题，本文引入了自适应缩减因子$w$，实现了缩减因子的动态调整。
$$w={\mathrm{e}}^{-\frac{b}{k^a}\frac{t}{T_{\max }}}$$

在滚球蜣螂阶段，个体更新：
$${\mathbf{x}}_i(t+1)=w{\mathbf{x}}_i(t)+\alpha k{\mathbf{x}}_i(t-1)+b\Delta \mathbf{x}$$
$${\mathbf{x}}_i(t+1)=w{\mathbf{x}}_i(t)+\tan \theta \left|{\mathbf{x}}_i(t)-{\mathbf{x}}_i(t-1)\right|$$

动态边界的分数阶调整

DBO上下边界会随着迭代动态收缩，从而提升搜索的精度。但随着边界的不断收窄，种群个体容易集中甚至重叠，导致多样性下降，影响全局优化能力。此外，当前边界的调整仅依赖于当前迭代次数以及局部和全局最优解的位置，缺乏对历史边界信息的继承和利用，进一步限制了优化效果。采用G-L定义：
$$D^v[f(x)]=\underset{\omega \to 0}{\lim }{\omega }^{-v}\sum _{k=0}^{\beta }(-1{)}^k\frac{\Gamma (v+1)}{\Gamma (k+1)\Gamma (v-k+1)}f(x-k\omega )$$

化简可得：
$$D^{\nu }\left[L{b}^{\ast }(t+1)\right]=\left(\frac{1}{T_{\text{max}}}\right){\mathbf{X}}^{\ast }$$
$$D^{\nu }\left[U{b}^{\ast }(t+1)\right]=-\left(\frac{1}{T_{\text{max}}}\right){\mathbf{X}}^{\ast }$$

重复更新机制

重复更新机制通过对全局最优个体的位置进行多次迭代更新，结合局部最优和群体平均信息，并引入概率性多样化操作，有效提升了算法跳出局部最优的能力。

4.结果展示

这里采用fes对FORDBO测试（原文iter，增加DE冠军算法）

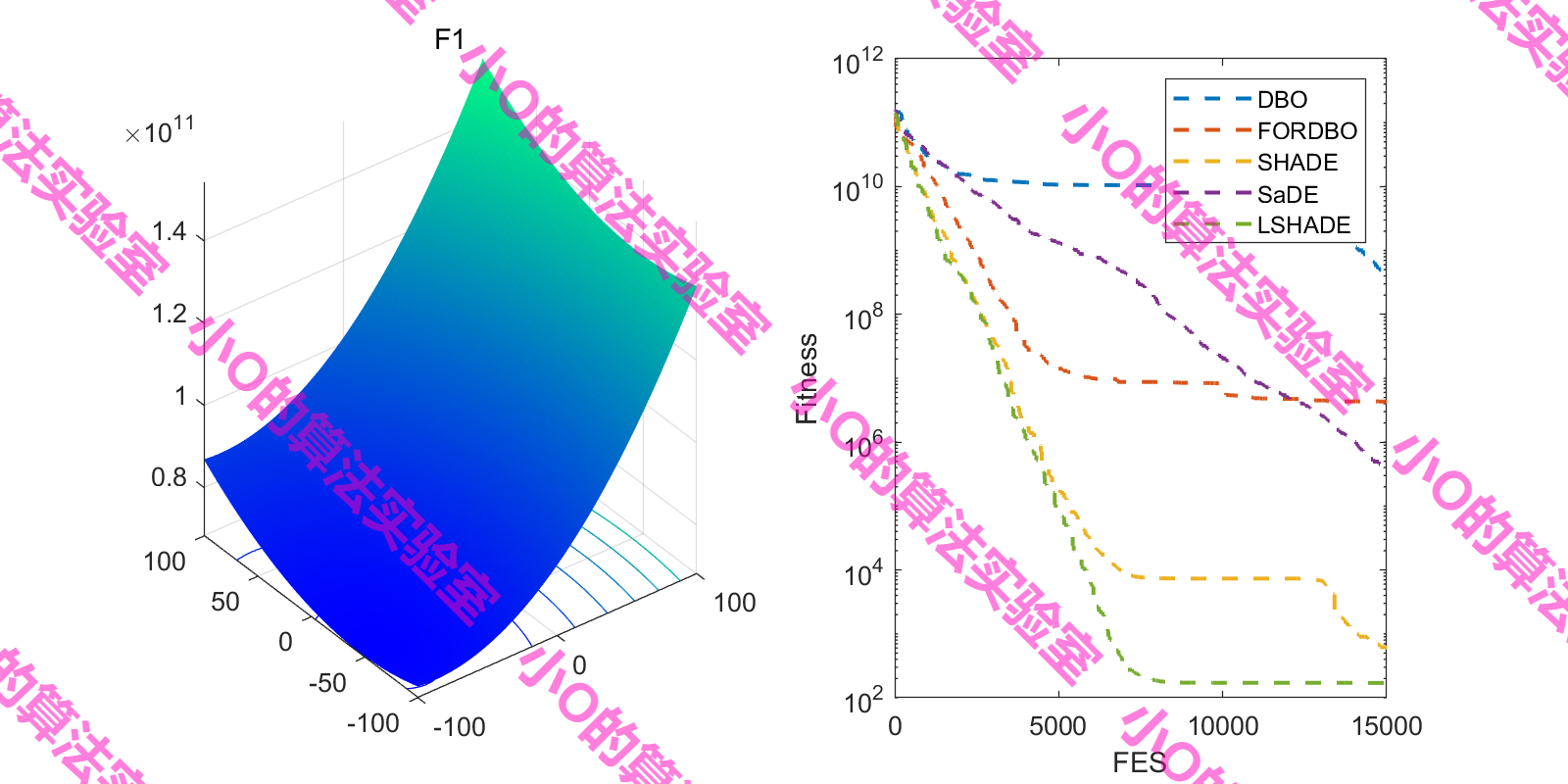
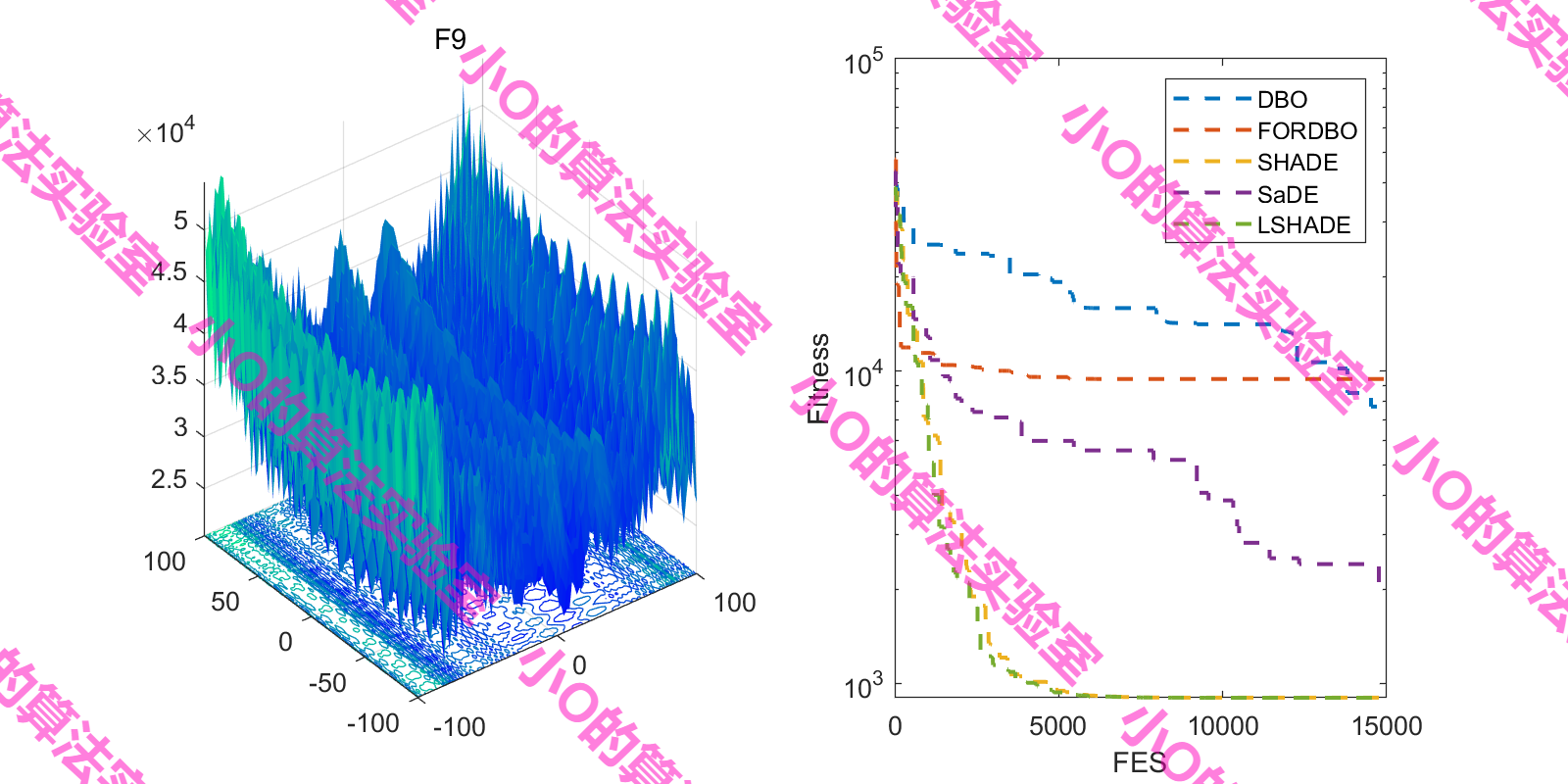
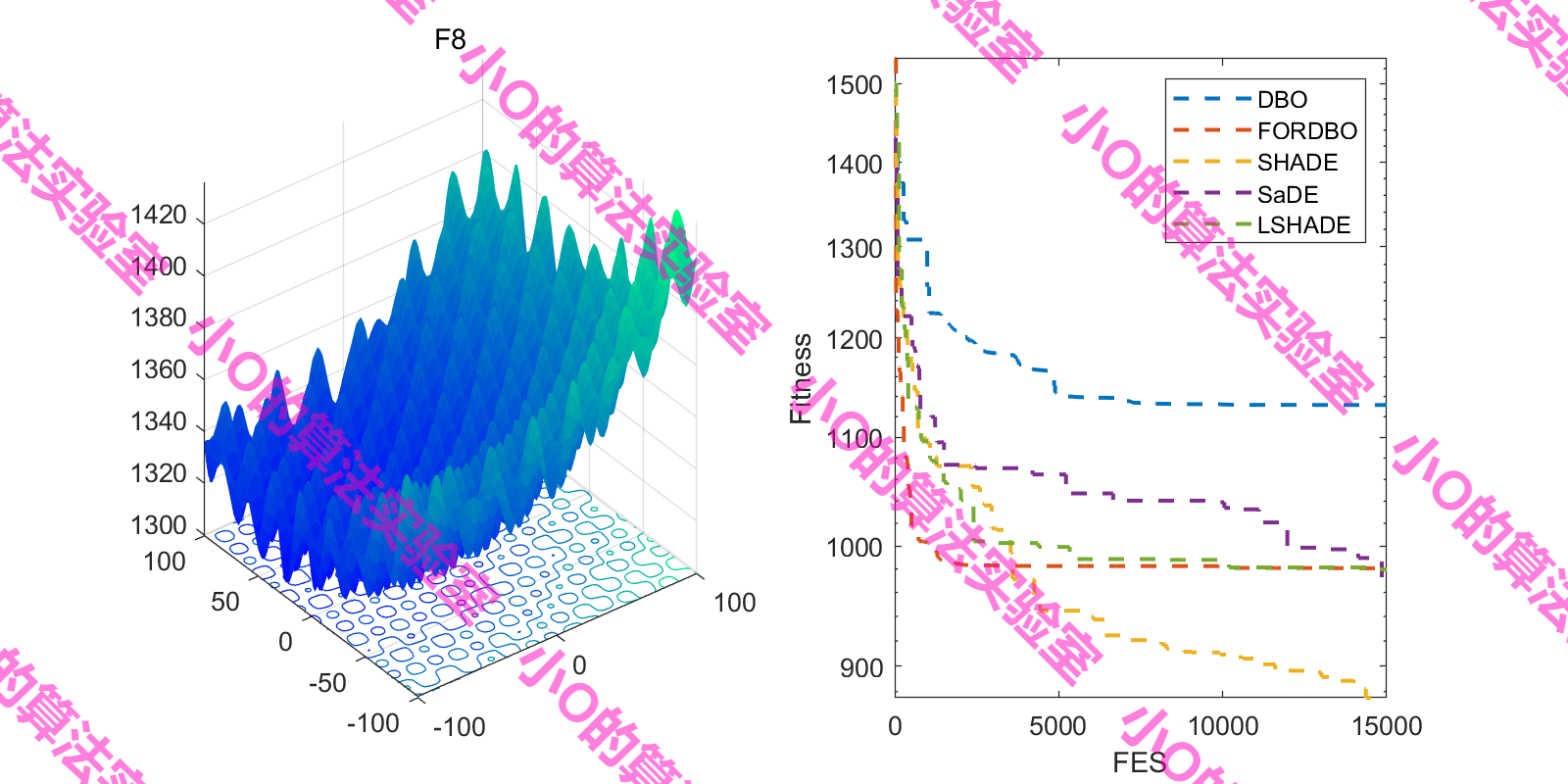
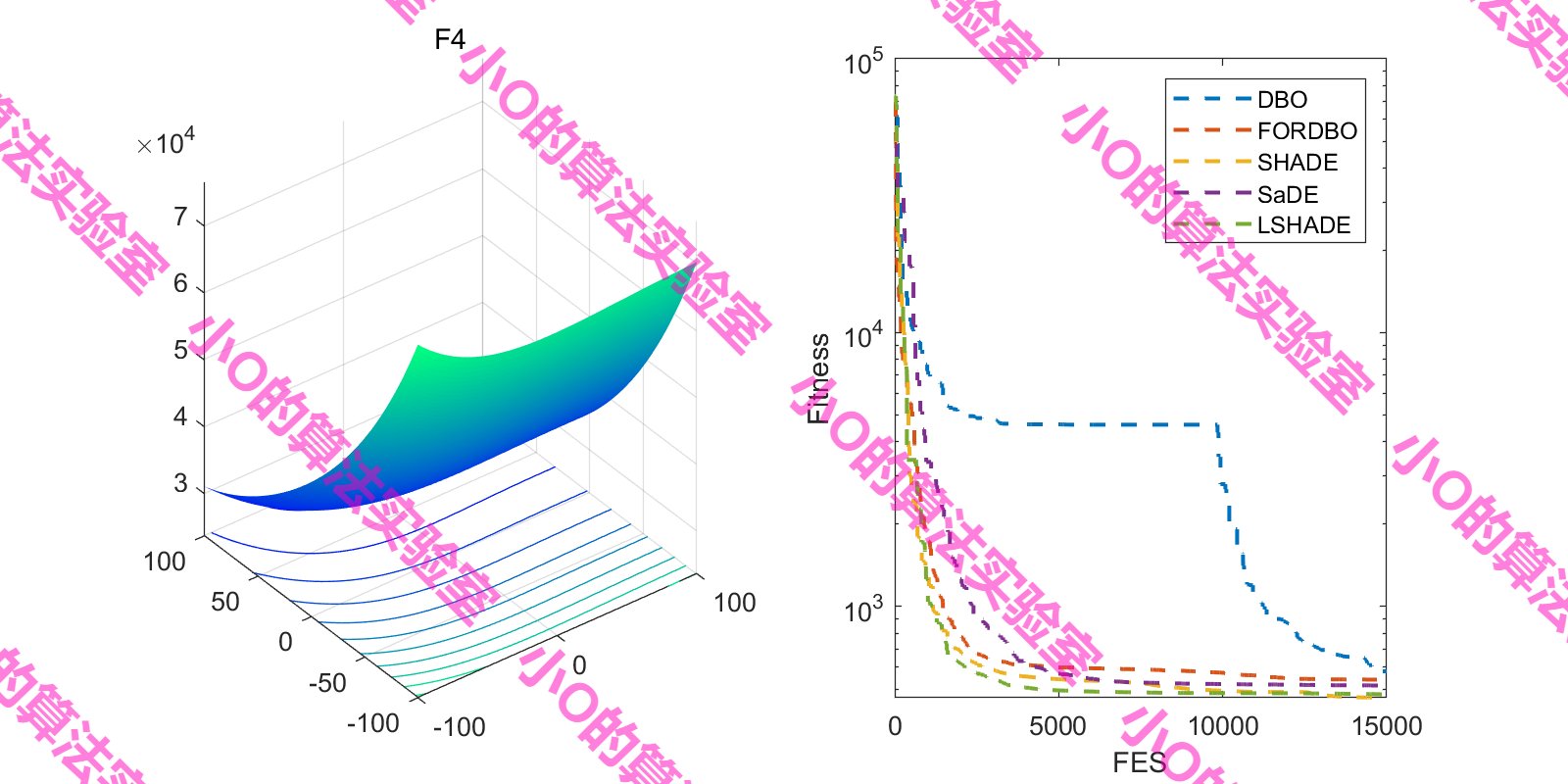
5.参考文献

[1] Xia H, Ke Y, Liao R, et al. Fractional order dung beetle optimizer with reduction factor for global optimization and industrial engineering optimization problems[J]. Artificial Intelligence Review, 2025, 58(10): 308.

6.代码获取

xx

7.算法辅导·应用定制·读者交流