1、矩阵置零

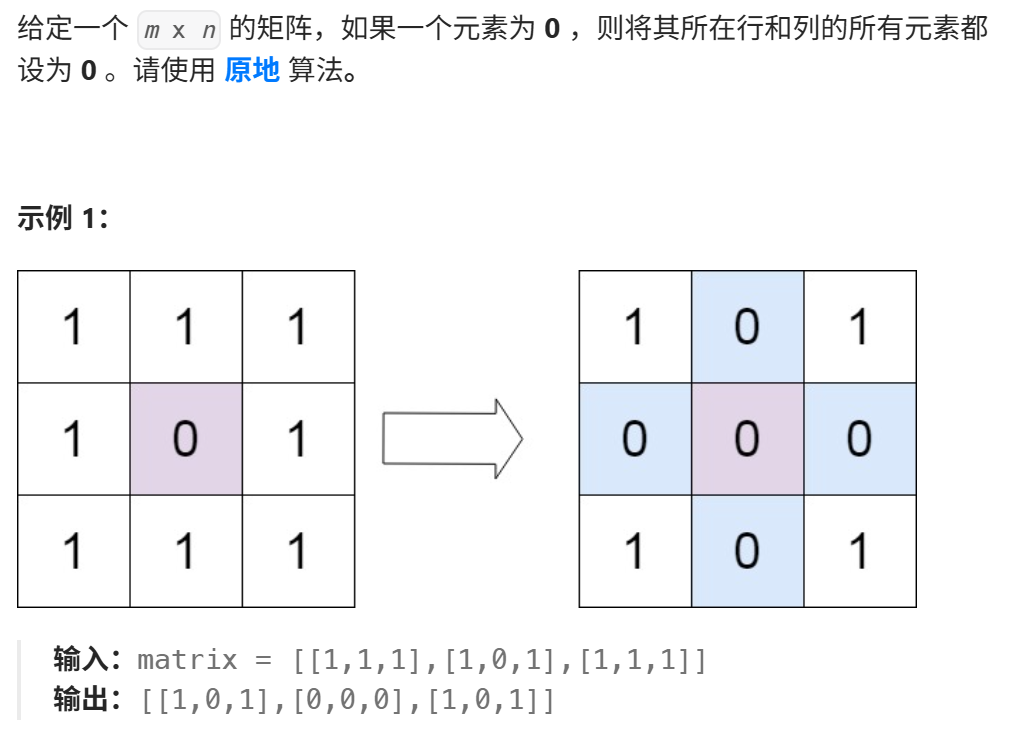
解题思路：这道题核心是要确定哪些行和哪些列要置零。所以定义两个数组，一个记录要置零的行，一个记录要置零的列。遍历整个矩阵，如果当前位置是0的话，就令l[i]=1,r[j]=1，之后再遍历l数组和r数组，并且对原数组置零。

class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length;int n  = matrix[0].length;int []l = new int[m];int []r = new int[n];//找到要置零的行和列for(int i = 0;i<m;i++){for(int j=0;j<n;j++){if(matrix[i][j]==0){l[i]=1;r[j]=1;}}}//遍历行，确定哪一行要置零for(int i = 0;i<m;i++){if(l[i]==1){for(int j =0;j<n;j++){matrix[i][j]=0;}}}//遍历列，确定哪一列要置零for(int j = 0;j<n;j++){if(r[j]==1){for(int i =0;i<m;i++){matrix[i][j]=0;}}}}
}

2、螺旋矩阵

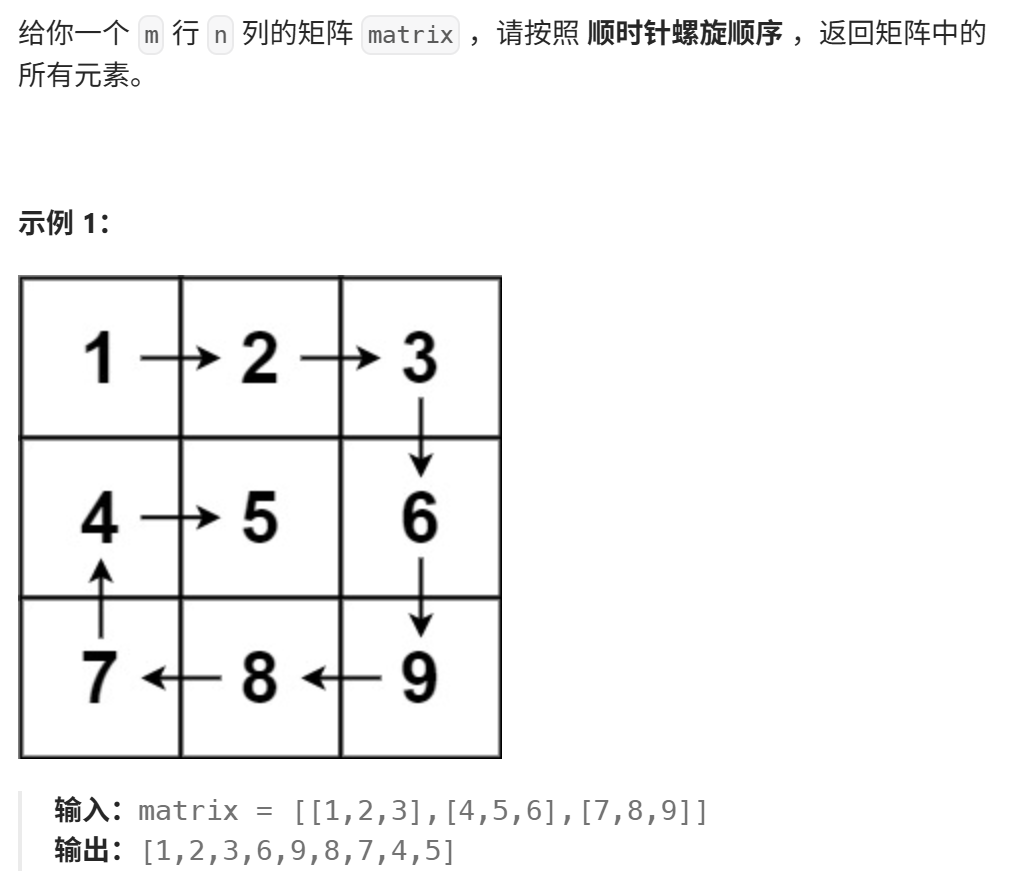
解题思路：这道题要确定上下左右的边界值，依次遍历整个矩阵。

class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();int m = matrix.length;int n = matrix[0].length;int top = 0,bottom = m-1;int left = 0,right = n-1;while(top<=bottom&&left<=right){//加入上面的一行for(int j = left;j<=right;j++){result.add(matrix[top][j]);}top++;//加入左边的一列for(int i = top;i<=bottom;i++){result.add(matrix[i][right]);}right--;//加入下面的一行if(top<=bottom){for(int j = right;j>=left;j--){result.add(matrix[bottom][j]);}bottom--;}//加入左边的一列if(left<=right){for(int i = bottom;i>=top;i--){result.add(matrix[i][left]);}left++;}}return result;}
}

3、旋转图像

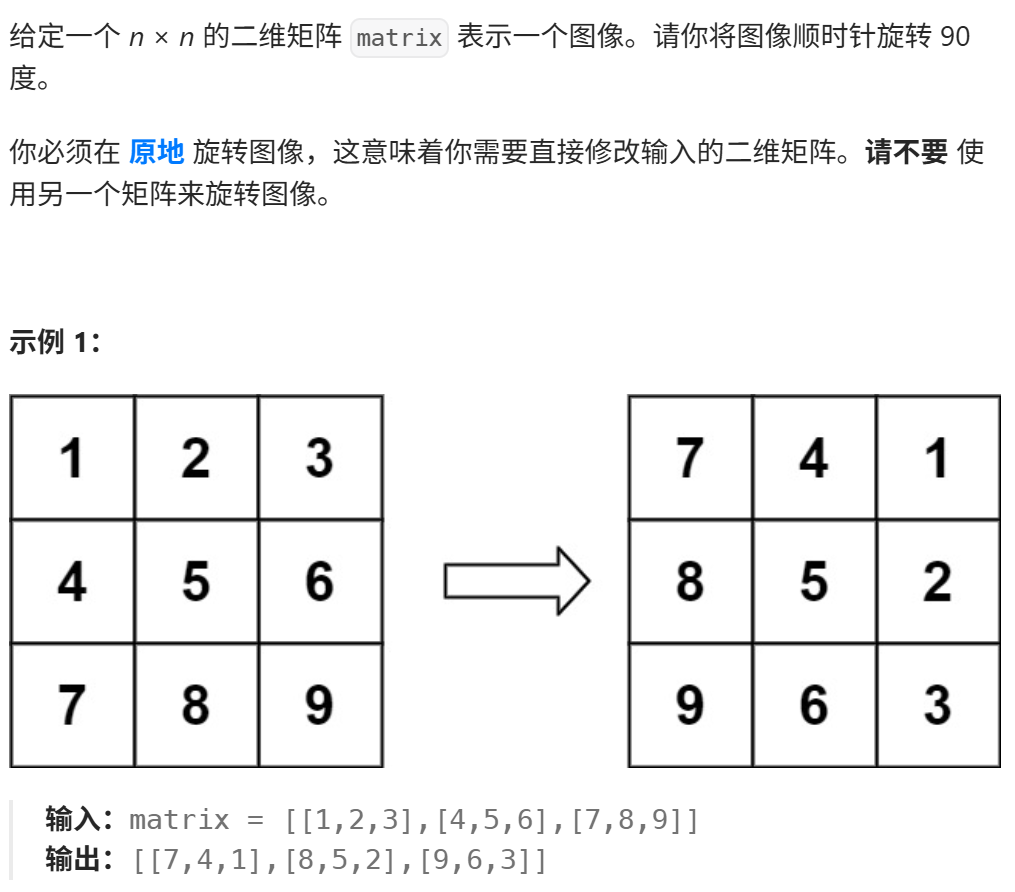
解题思路：先将一行存储到一个数组中去，依次遍历整个矩阵，左列最后两个到上行的左边两个，下列的最后两个到左列的最后两个，右列的上面两个到下列的右边两个，上列存储的到右列的上面两个。

class Solution {public void rotate(int[][] matrix) {int n = matrix.length;int left = 0;int right = n - 1;int top = 0;int bottom = n - 1;// 每一圈旋转while (left < right && top < bottom) {int len = right - left;int[] tmp = new int[len];  // 保存当前层顶部行（不含最后一个元素）// 1. 保存 top 行的前 len 个元素（右上角那个位置留给最后赋值）for (int j = 0; j < len; j++) {tmp[j] = matrix[top][left + j];}// 2. 左列 → 上行for (int i = 0; i < len; i++) {matrix[top][left + i] = matrix[bottom - i][left];}// 3. 下行 → 左列for (int j = 0; j < len; j++) {matrix[bottom - j][left] = matrix[bottom][right - j];}// 4. 右列 → 下行for (int i = 0; i < len; i++) {matrix[bottom][right - i] = matrix[top + i][right];}// 5. tmp（原 top 行） → 右列for (int j = 0; j < len; j++) {matrix[top + j][right] = tmp[j];}// 收缩一圈left++;right--;top++;bottom--;}}
}

4、搜索二维矩阵

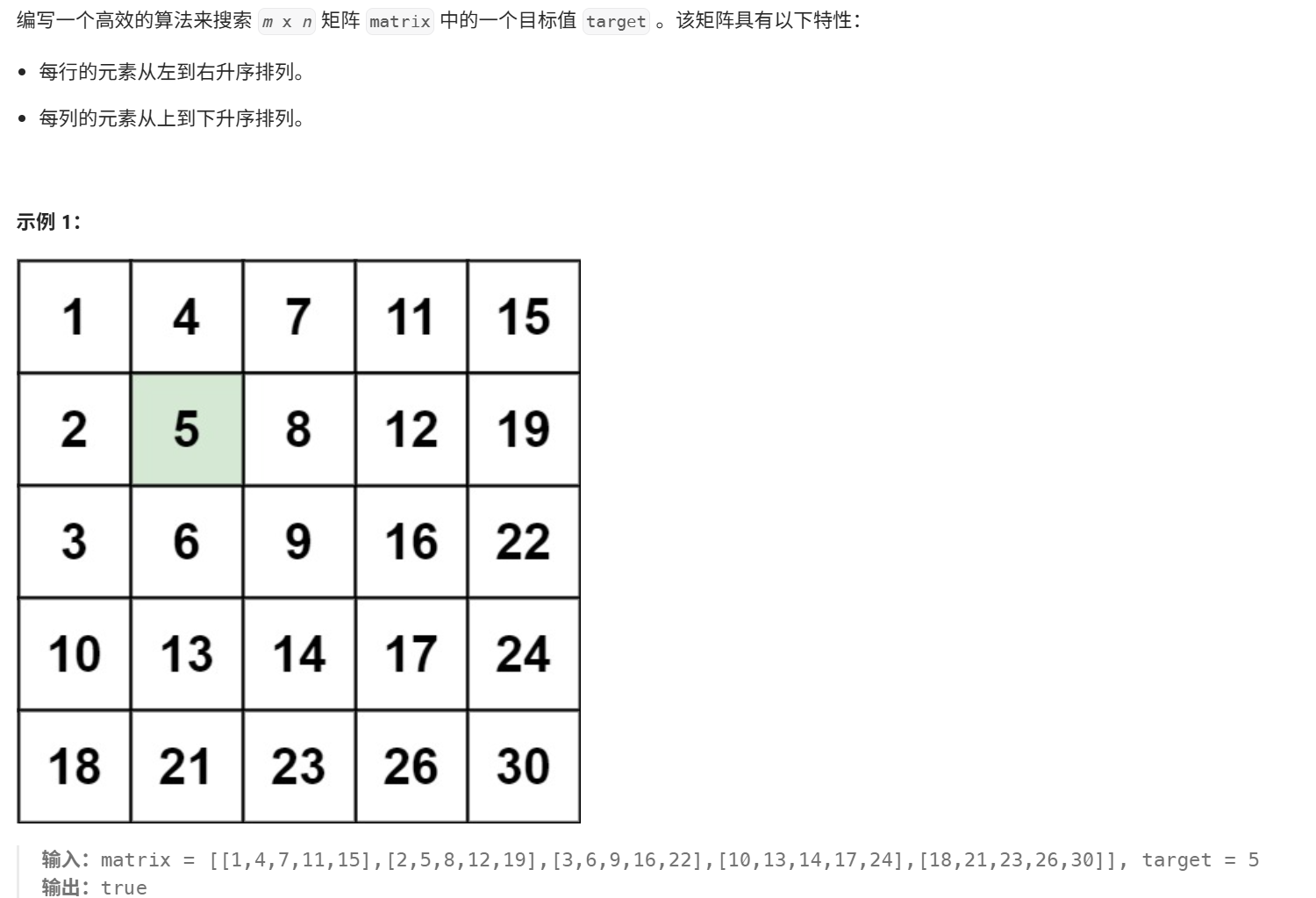
解题思路：从右上角开始判断，如果target小于这个数，就往左移，如果target大于这个数就往下移。因为最右上角是这一行的最大值，也是这一列的最小值。

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length;int n = matrix[0].length;int top = 0;int right = n-1;while(top<m&&right>=0){if(target>matrix[top][right]){top++;}else if(target<matrix[top][right]){right--;}else{return true;}}return false;}
}