文章链接

1049. 最后一块石头的重量 II

解题关键：找到重量和尽量相等的两堆

1. 确定dp数组以及下标的含义

• dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

1. 确定递推公式

• 01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

• 本题则是：dp[j] =max(dp[j], dp[j - stones[i]] + stones[i])

1. dp数组初始化

2. 确定遍历顺序

public class Solution {public int LastStoneWeightII(int[] stones) {int[] dp=new int[15001];int sum=0;foreach(int stone in stones){sum+=stone;}int target=sum/2;for(int i=0;i<stones.Length;i++){for(int j=target;j>=stones[i];j--){dp[j]=Math.Max(dp[j],dp[j-stones[i]]+stones[i]);}}return sum-2*dp[target];}
}

494.目标和

加法集合left，减法集合right

left+right=sum

left-right=target

righ=sum-left

left-(sum-left)=target

left=(target+sum)/2

递推公式：

二维DP数组递推公式： dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];

去掉维度i 之后，递推公式：dp[j] = dp[j] + dp[j - nums[i]] ，即：dp[j] += dp[j - nums[i]]

public class Solution {public int FindTargetSumWays(int[] nums, int target) {int sum=0;foreach(int num in nums){sum+=num;}// 如果目标绝对值大于总和，无法组成if (Math.Abs(target) > sum) return 0;// 如果总和加目标值为奇数，无法整除2，无解if ((sum + target) % 2 == 1) return 0;// 计算背包容量，即子集P的和int bagSize = (sum + target) / 2;// dp[j]表示和为j的子集数量int[] dp = new int[bagSize + 1];// 和为0的子集只有一种情况：空集dp[0] = 1;for(int i=0;i<nums.Length;i++){for(int j = bagSize; j >= nums[i]; j--){dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
}

474.一和零

dp[i][j]：装满i个0，j个1最大有dp[i][j]个物品

递推公式：dp[i][j]=max(dp[i-x][j-y]+1,dp[i,j]

初始化：dp[0][0]=0

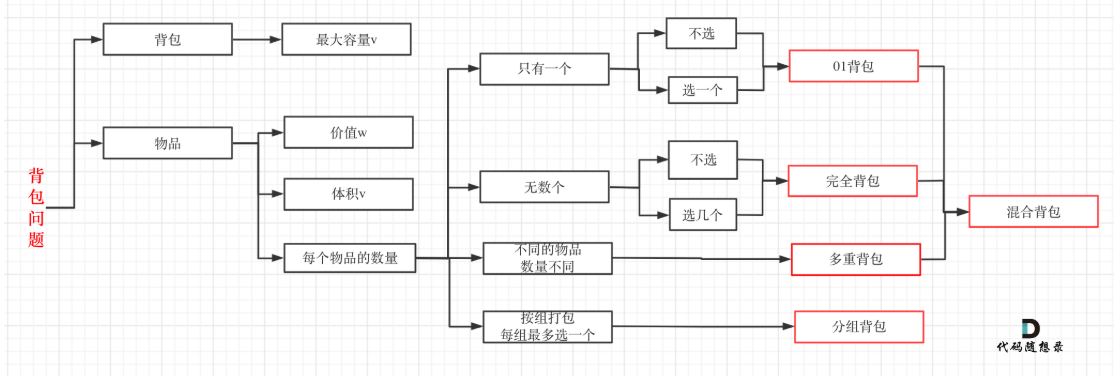
总结

• 纯 0 - 1 背包 (opens new window)是求 给定背包容量 装满背包 的最大价值是多少。

• 416. 分割等和子集 (opens new window)是求 给定背包容量，能不能装满这个背包。

• 1049. 最后一块石头的重量 II (opens new window)是求 给定背包容量，尽可能装，最多能装多少

• 494. 目标和 (opens new window)是求 给定背包容量，装满背包有多少种方法。

• 本题是求 给定背包容量，装满背包最多有多少个物品。

public class Solution
{public int FindMaxForm(string[] strs, int m, int n){// 问题：从字符串数组中选出最多的字符串，使其包含的0不超过m个，1不超过n个// 这是一个二维01背包问题：每个字符串是一个物品，有两个重量参数(0的数量和1的数量)// 背包容量限制为m(0的最大数量)和n(1的最大数量)// dp[i,j]表示使用i个0和j个1时能容纳的最大字符串数量int[,] dp = new int[m + 1, n + 1];// 遍历每个字符串(物品)foreach (string str in strs){// 统计当前字符串中0和1的数量int zero = 0, one = 0;foreach (char c in str){if (c == '0') zero++;else one++;}// 二维01背包的倒序遍历，防止重复使用同一物品// 从大到小遍历0的数量for (int i = m; i >= zero; i--){// 从大到小遍历1的数量for (int j = n; j >= one; j--){// 状态转移方程：// 不选当前字符串：保持dp[i,j]不变// 选当前字符串：dp[i-zero, j-one] + 1(加1表示选了当前字符串)// 取两种选择的最大值dp[i, j] = Math.Max(dp[i, j], dp[i - zero, j - one] + 1);}}}// 返回使用不超过m个0和n个1时能容纳的最大字符串数量return dp[m, n];}
}